Chapter 14: Parameter Estimation with Prior Probabilities

Author

Zane Billings

Published

2024-07-29

options("scipen" = 9999, "digits" = 4)

Q1

Suppose you’re playing air hockey with some friends and flip a coin to see who starts with the puck. After playing 12 times, you realize that the friend who brings the coin almost always seems to go first: 9 out of 12 times. Some of your other friends start to get suspicious. Define prior probability distributions for the following beliefs:

  1. One person who weakly believes that the friend is cheating and the true rate of coming up heads is closer to 70 percent.
  2. One person who very strongly trusts that the coin is fair and provided a 50 percent chance of coming up heads.
  3. One person who strongly believes the coin is biased to come up heads 70 percent of the time.

We’ll use a beta distribution for all three of the priors. For the first prior, we want a beta distribution with a mean that’s close to 70 percent, but we want the variance to be fairly high. The easiest way to do this, is to use \(\alpha = 7\) and \(\beta = 3\), which we know will have a mean of exactly \(70\%\) but will still be fairly spread out.

For the second prior, we’ll use a beta distribution with equal parameters. Since their belief is fairly strong, we’ll say \(\alpha = 10\), \(\beta = 10\). Finally, for the third person, we’ll use \(\alpha = 700\), \(\beta = 300\), which will have a mean of \(70\%\) but with little variation.

Let’s plot the three priors. The code for this plot is somewhat long, so it has been hidden by default.

Code 
# Setup
pal <- gray.colors(3, start = 0, end = 0.75)
xs <- seq(1e-5, 1 - 1e-5, length.out = 1000)
layout(matrix(c(1, 2), nrow = 1))

# PDF plot
p1 <- dbeta(xs, 7, 3)
p2 <- dbeta(xs, 10, 10)
p3 <- dbeta(xs, 700, 300)
plot(
    NULL, NULL,
    xlab = "Probability of the coin being heads",
    ylab = "Prior density (truncated at 4)",
    xlim = c(0, 1), ylim = c(0, 4),
    axes = FALSE,
    main = "Friends' prior PDFs"
)
lines(xs, p1, lwd = 3, col = pal[[1]], lty = 1)
lines(xs, p2, lwd = 3, col = pal[[2]], lty = 2)
lines(xs, p3, lwd = 3, col = pal[[3]], lty = 3)
axis(1, seq(0, 1, 0.25))
axis(2, seq(0, 4, 1))
legend(
    x = 0, y = 3.9,
    legend = c("Friend 1", "Friend 2", "Friend 3"),
    col = pal,
    lty = 1:3,
    lwd = 3
)

# CDF plot
c1 <- pbeta(xs, 7, 3)
c2 <- pbeta(xs, 10, 10)
c3 <- pbeta(xs, 700, 300)
plot(
    NULL, NULL,
    xlab = "Probability of the coin being heads",
    ylab = "Cumulative prior probability",
    xlim = c(0, 1), ylim = c(0, 1),
    axes = FALSE,
    main = "Friends' prior CDFs"
)
lines(xs, c1, lwd = 3, col = pal[[1]], lty = 1)
lines(xs, c2, lwd = 3, col = pal[[2]], lty = 2)
lines(xs, c3, lwd = 3, col = pal[[3]], lty = 3)
axis(1, seq(0, 1, 0.25))
axis(2, seq(0, 1, 0.25))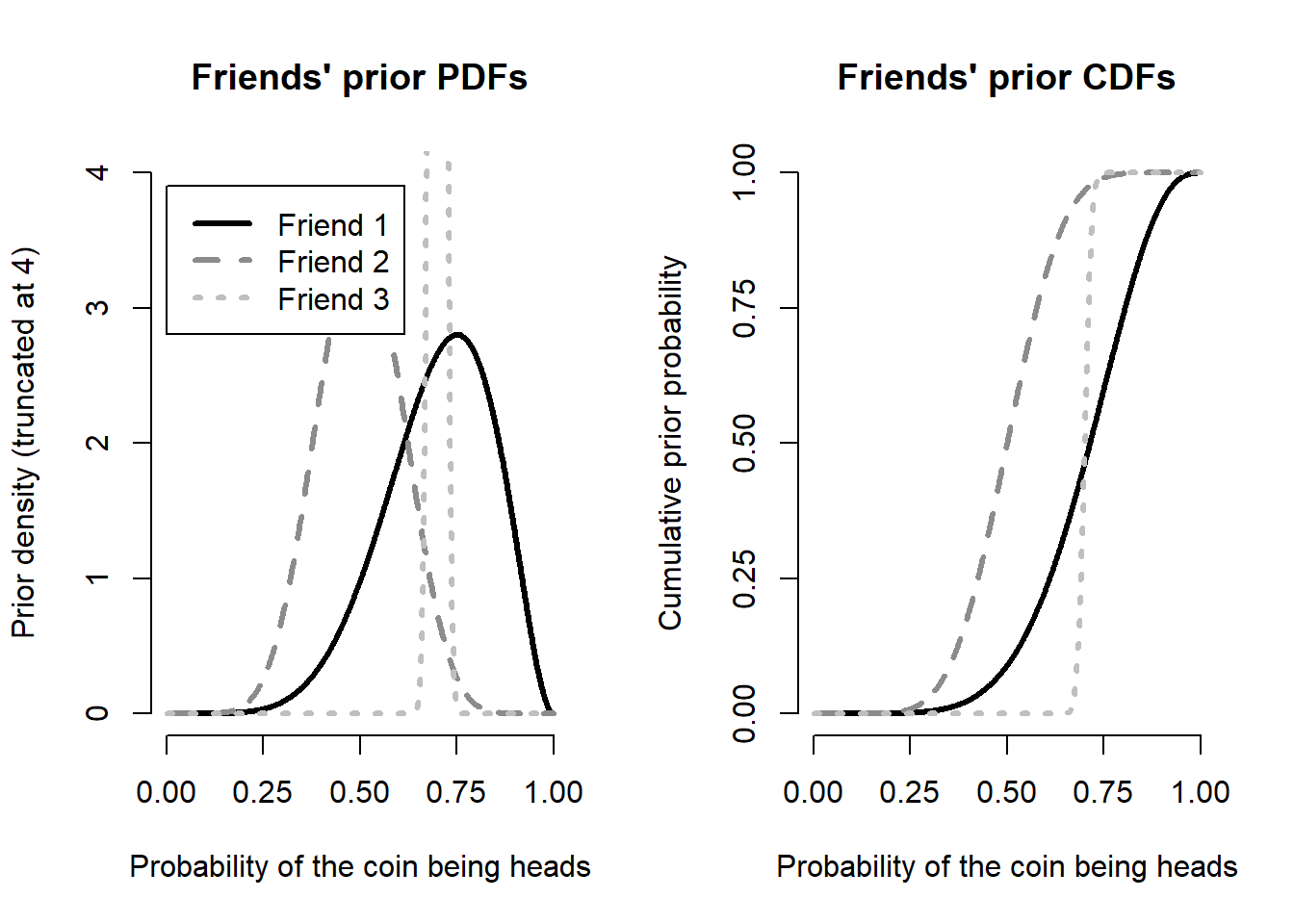

We can see that friend 3 is so certain, the PDF plot had to be truncated in order to see the other two curves.

To test the coin, you flip it 20 more times and get 9 heads and 11 tails. Using the priors you calculated in the previous question, what are the updated posterior beliefs in the true rate of flipping a heads in terms of the 95 percent confidence interval?

OK. now we need to compute the posteriors for each of the three friends.

post1 <- dbeta(xs,  7 + 9,  3 + 11)
post2 <- dbeta(xs, 10 + 9, 10 + 11)
post3 <- dbeta(xs, 70 + 9, 30 + 11)

Next we need to calculate the posterior credible intervals.

ci_levels <- c(0.025, 0.975)
post_cis <-
    rbind(
        qbeta(ci_levels, 07 + 9, 03 + 11),
        qbeta(ci_levels, 10 + 9, 10 + 11),
        qbeta(ci_levels, 70 + 9, 30 + 11)
    ) |>
    `colnames<-`(c("lower", "upper")) |>
    tibble::as_tibble() |>
    tibble::add_column(friend = paste(1:3))
print(post_cis)
# A tibble: 3 × 3
  lower upper friend
  <dbl> <dbl> <chr> 
1 0.357 0.706 1     
2 0.324 0.628 2     
3 0.572 0.740 3

Finally, we can visualize the prior and posterior density with the CrI for each of our friends.

Code 
# Setup
pal2 <- gray.colors(2, start = 0, end = 0.5)
xs <- seq(1e-5, 1 - 1e-5, length.out = 1000)
layout(matrix(c(1, 2, 3), nrow = 1))

# posterior/prior plots
# Friend 1
plot(
    NULL, NULL,
    main = "Friend 1",
    xlim = c(0, 1), ylim = c(0, 10),
    xlab = "Probability of the coin being heads",
    ylab = "Density",
)
lines(xs, p1,    lwd = 3, col = pal2[[2]], lty = 3)
lines(xs, post1, lwd = 3, col = pal2[[1]], lty = 1)
abline(v = post_cis[[1, 1]], lty = 2, lwd = 1, col = "firebrick2")
abline(v = post_cis[[1, 2]], lty = 2, lwd = 1, col = "firebrick2")

legend(
    x = 0.02, y = 9.75,
    legend = c("Prior", "Posterior", "95% CrI"),
    col = c(rev(pal2), "firebrick2"),
    lty = c(3, 1, 2),
    lwd = c(3, 3, 1)
)

# Friend 2
plot(
    NULL, NULL,
    main = "Friend 2",
    xlim = c(0, 1), ylim = c(0, 10),
    xlab = "Probability of the coin being heads",
    ylab = "Density",
)
lines(xs, p2,    lwd = 3, col = pal2[[2]], lty = 3)
lines(xs, post2, lwd = 3, col = pal2[[1]], lty = 1)
abline(v = post_cis[[2, 1]], lty = 2, lwd = 1, col = "firebrick2")
abline(v = post_cis[[2, 2]], lty = 2, lwd = 1, col = "firebrick2")

# Friend 3
plot(
    NULL, NULL,
    main = "Friend 3",
    xlim = c(0, 1), ylim = c(0, 10),
    xlab = "Probability of the coin being heads",
    ylab = "Density",
)
lines(xs, p3,    lwd = 3, col = pal2[[2]], lty = 3)
lines(xs, post3, lwd = 3, col = pal2[[1]], lty = 1)
abline(v = post_cis[[3, 1]], lty = 2, lwd = 1, col = "firebrick2")
abline(v = post_cis[[3, 2]], lty = 2, lwd = 1, col = "firebrick2")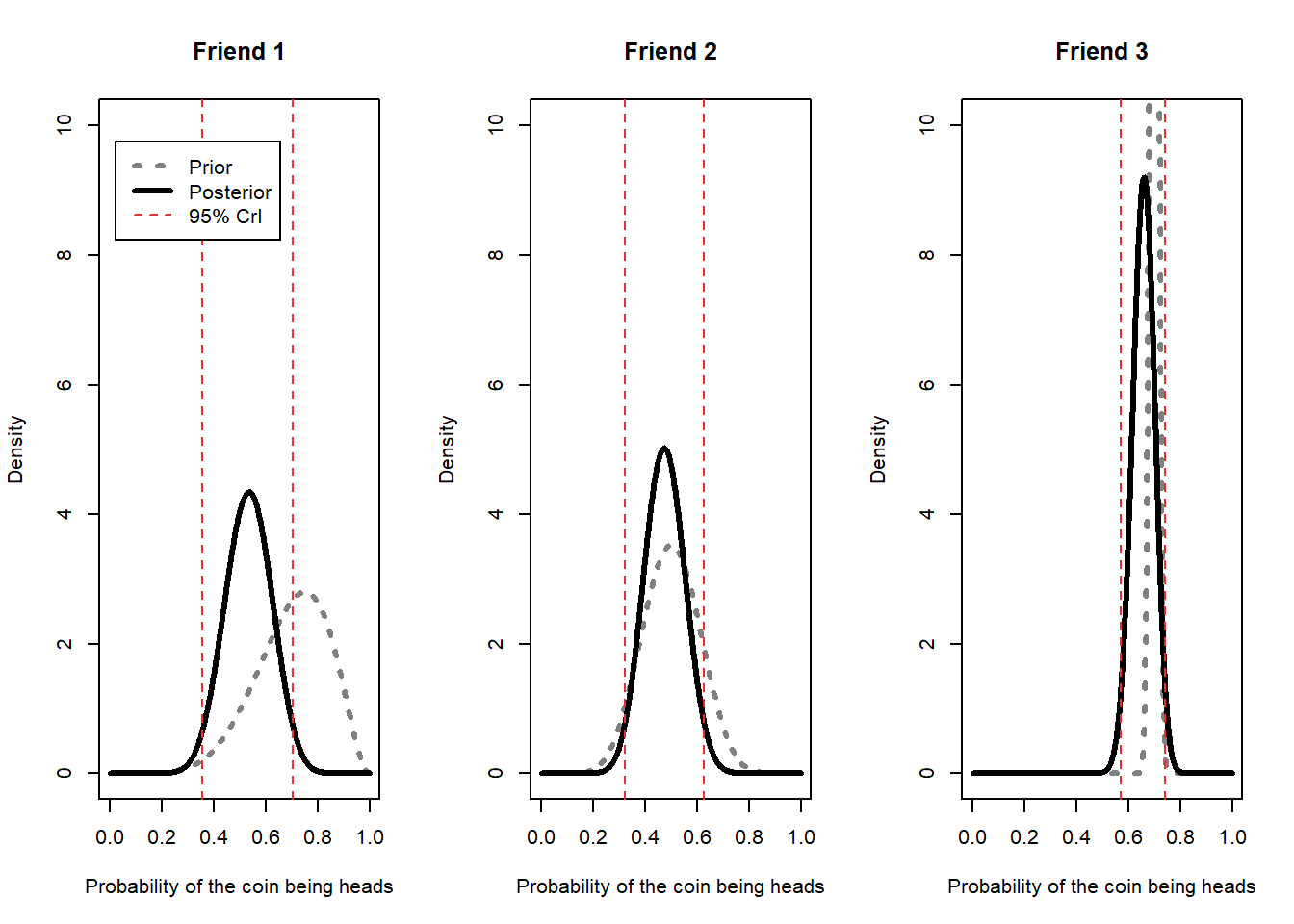

Overall, we can see the following conclusions for each friend:

  1. Friend 1 did think the coin was unfair before, but is now much more willing to believe the coin is fair given the observed data;
  2. Friend 2 thought the coin was fair before and is now more confident that the coin is fair given the observed data; and
  3. Friend 3 still strongly believes the coin is unfair, but the observed data is beginning to change their mind – they are at least now willing to entertain the possibility that the coin is fair.