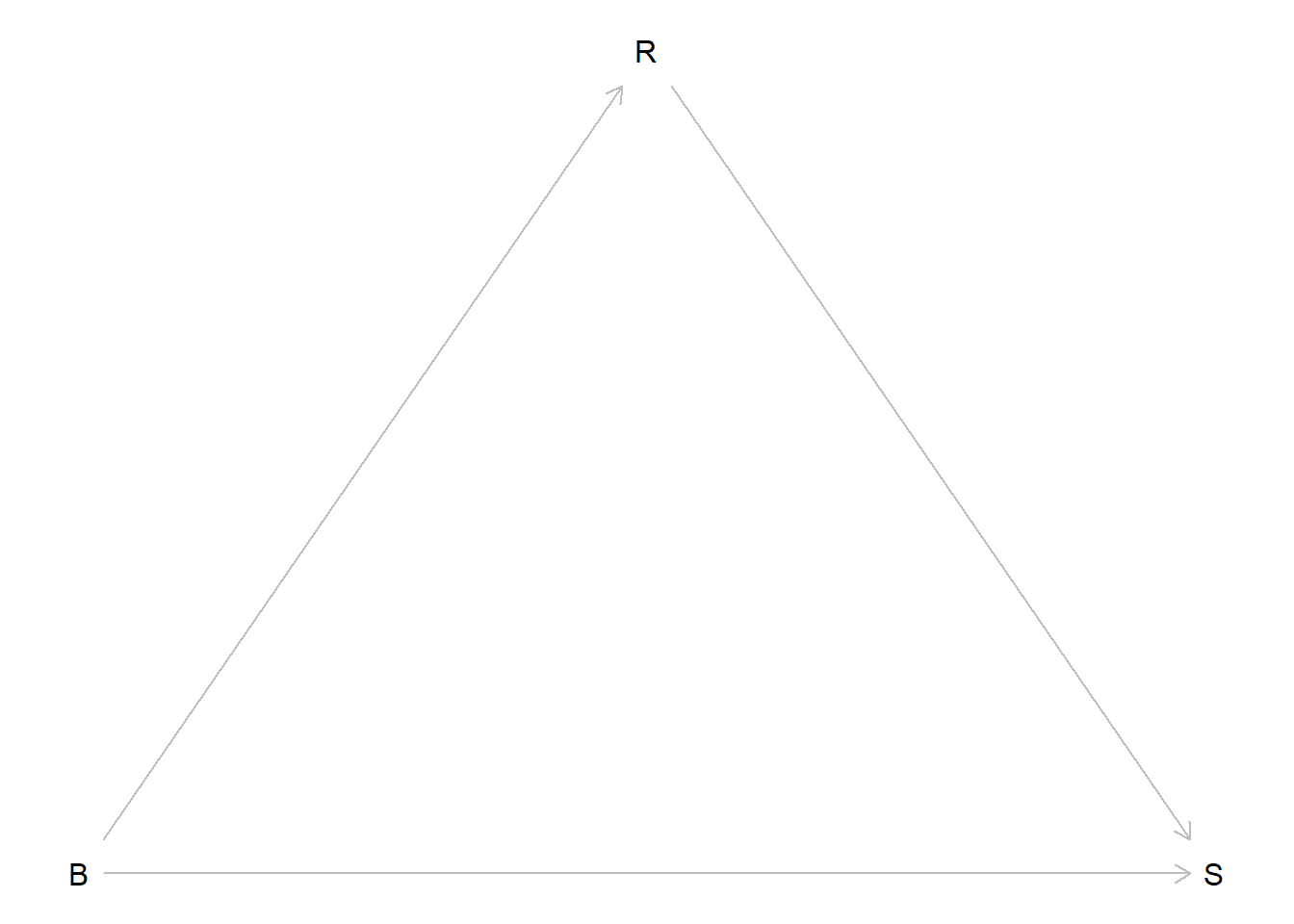
This chapter covers common models for count data: bernoulli models, aggregated binomial models, Poisson and gamma-Poisson models, and multinomial/categorical models.
Exercises
11E1
If an event has probability 0.35, then the log-odds of the event are \[\mathrm{logit}\ 0.35 = \log \frac{0.35}{1 - 0.35} \approx -0.62.\]
11E2
If an event has log-odds 3.2, the probability of the event is \[\mathrm{logit}^{-1}\ 3.2 = \frac{\exp 3.2}{1 + \exp3.2} \approx 0.96\]
11E3
If the coefficient in a logistic regression has value 1.7, this implies that the log-odds of the outcome increase by 1.7 for every one-unit change in the predictor associated with that coefficient; or that the odds of the outcome are multiplied by \(\exp 1.7 \approx 5.47\) for every one-unit change in the predictor.
11E4
Poisson regressions require the use of an offset when different outcome observations are associated with different exposure times; or in other words, when you want to model rates instead of counts (of course when we model counts without an offset, we are also modeling rates but all the denominators are constant). For example, if you monitor the number of positive influenza diagnostic tests at multiple clinics, you need to use an offset that models the total number of flu tests performed at each clinic, or at least the total number of visitors. (We could also model this as a binomial outcome, but that is true for a lot of Poisson problems.)
11M1
When we reorganize data from the disaggregated to the aggregated binomial form, the likelihood changes because we also account for the number of potential ways to get the same aggregate outcome. The disaggregated model only considers the outcome for the specific order of event occurrences that we observed, while the aggregated model gives the likelihood for any sample with the same number of cases, which could have potentially arisen in many ways.
That means we should use the aggregated binomial form only when we truly know that any samples with the same number of cases is identical – for example, if our experimental units are individuals and we know which individuals experienced an outcome, these data would be disaggregate because we could potentially have other information that explains differences between individuals.
11M2
If a coefficient in a Poisson regression has value 1.7, assuming the typical log link function, that implies that a one unit change in the associated predictor leads to a \(\exp 1.7 \approx 5.47\) -fold change in the outcome; or an equivalent \(5.47\) -fold change in the rate of outcome occurrence.
11M3
The logit link is typically appropriate for a binomial GLM because we apply a linear model to the parameter \(p\) , which is a probability. The logit link is a function that maps \((0, 1) \to \mathbb{R}\) , and all probabilities have to be in the interval \([0, 1]\) . So the logit link ensures that the real-valued linear predictor is mapped to the allowed domain of the parameter \(p\) .
11M4
The log link is typically appropriate for a Poisson GLM because we apply a linear model to the only parametr \(\lambda\) , which only has support on \((0, \infty)\) . The log link function maps the input from \((0, \infty) \to \mathbb{R}\) , so \(\log \lambda\) and the linear predictor have the same allowed values.
11M5
Using a logit link for the mean of a Poisson GLM would imply that \(\lambda \in (0, 1)\) is a necessary constraint for the problem. When \(\lambda < 1\) , the highest probility value for the Poisson distribution is 0, so we would want to do this on data where we know a priori that \(0\) is the most common outcome, but larger numbers can happen.
11M6
The binomial distribution has maximum entropy when the data have two possible values and the expected value is constant (i.e., when the probability of each outcome is constant). Since the Poisson distribution is a special limiting case of the binomial distribution, it must have the same maximum entropy conditions.
11M7
We’ll recreate the chimpanzee model using both quap (quadratic approximation) and ulam (HMC) to compare the differences between the fitting methods.
data (chimpanzees, package = "rethinking" )<- chimpanzees$ treatment <- 1 + d$ prosoc_left + 2 * d$ condition<- list (pulled_left = d$ pulled_left,actor = d$ actor,treatment = as.integer (d$ treatment)<- alist (~ dbinom (1 , p),logit (p) <- a[actor] + b[treatment],~ dnorm (0 , 1.5 ),~ dnorm (0 , 0.5 ).4 _quap <- rethinking:: quap (flist = chimp_model,data = dat_list.4 _ulam <- rethinking:: ulam (flist = chimp_model,data = dat_list,chains = 4 ,log_lik = TRUE
In file included from stan/src/stan/model/model_header.hpp:5:
stan/src/stan/model/model_base_crtp.hpp:205:8: warning: 'void stan::model::model_base_crtp<M>::write_array(stan::rng_t&, std::vector<double>&, std::vector<int>&, std::vector<double>&, bool, bool, std::ostream*) const [with M = ulam_cmdstanr_78180b32ba80da6bc9c4f0f8342b99b3_model_namespace::ulam_cmdstanr_78180b32ba80da6bc9c4f0f8342b99b3_model; stan::rng_t = boost::random::mixmax_engine<17, 36, 0>; std::ostream = std::basic_ostream<char>]' was hidden [-Woverloaded-virtual=]
205 | void write_array(stan::rng_t& rng, std::vector<double>& theta,
| ^~~~~~~~~~~
C:/Users/Zane/AppData/Local/Temp/RtmpSCWF6a/model-305c144d30df.hpp:492: note: by 'ulam_cmdstanr_78180b32ba80da6bc9c4f0f8342b99b3_model_namespace::ulam_cmdstanr_78180b32ba80da6bc9c4f0f8342b99b3_model::write_array'
492 | write_array(RNG& base_rng, std::vector<double>& params_r, std::vector<int>&
stan/src/stan/model/model_base_crtp.hpp:136:8: warning: 'void stan::model::model_base_crtp<M>::write_array(stan::rng_t&, Eigen::VectorXd&, Eigen::VectorXd&, bool, bool, std::ostream*) const [with M = ulam_cmdstanr_78180b32ba80da6bc9c4f0f8342b99b3_model_namespace::ulam_cmdstanr_78180b32ba80da6bc9c4f0f8342b99b3_model; stan::rng_t = boost::random::mixmax_engine<17, 36, 0>; Eigen::VectorXd = Eigen::Matrix<double, -1, 1>; std::ostream = std::basic_ostream<char>]' was hidden [-Woverloaded-virtual=]
136 | void write_array(stan::rng_t& rng, Eigen::VectorXd& theta,
| ^~~~~~~~~~~
C:/Users/Zane/AppData/Local/Temp/RtmpSCWF6a/model-305c144d30df.hpp:492: note: by 'ulam_cmdstanr_78180b32ba80da6bc9c4f0f8342b99b3_model_namespace::ulam_cmdstanr_78180b32ba80da6bc9c4f0f8342b99b3_model::write_array'
492 | write_array(RNG& base_rng, std::vector<double>& params_r, std::vector<int>&
Running MCMC with 4 sequential chains, with 1 thread(s) per chain...
Chain 1 Iteration: 1 / 1000 [ 0%] (Warmup)
Chain 1 Iteration: 100 / 1000 [ 10%] (Warmup)
Chain 1 Iteration: 200 / 1000 [ 20%] (Warmup)
Chain 1 Iteration: 300 / 1000 [ 30%] (Warmup)
Chain 1 Iteration: 400 / 1000 [ 40%] (Warmup)
Chain 1 Iteration: 500 / 1000 [ 50%] (Warmup)
Chain 1 Iteration: 501 / 1000 [ 50%] (Sampling)
Chain 1 Iteration: 600 / 1000 [ 60%] (Sampling)
Chain 1 Iteration: 700 / 1000 [ 70%] (Sampling)
Chain 1 Iteration: 800 / 1000 [ 80%] (Sampling)
Chain 1 Iteration: 900 / 1000 [ 90%] (Sampling)
Chain 1 Iteration: 1000 / 1000 [100%] (Sampling)
Chain 1 finished in 1.3 seconds.
Chain 2 Iteration: 1 / 1000 [ 0%] (Warmup)
Chain 2 Iteration: 100 / 1000 [ 10%] (Warmup)
Chain 2 Iteration: 200 / 1000 [ 20%] (Warmup)
Chain 2 Iteration: 300 / 1000 [ 30%] (Warmup)
Chain 2 Iteration: 400 / 1000 [ 40%] (Warmup)
Chain 2 Iteration: 500 / 1000 [ 50%] (Warmup)
Chain 2 Iteration: 501 / 1000 [ 50%] (Sampling)
Chain 2 Iteration: 600 / 1000 [ 60%] (Sampling)
Chain 2 Iteration: 700 / 1000 [ 70%] (Sampling)
Chain 2 Iteration: 800 / 1000 [ 80%] (Sampling)
Chain 2 Iteration: 900 / 1000 [ 90%] (Sampling)
Chain 2 Iteration: 1000 / 1000 [100%] (Sampling)
Chain 2 finished in 1.4 seconds.
Chain 3 Iteration: 1 / 1000 [ 0%] (Warmup)
Chain 3 Iteration: 100 / 1000 [ 10%] (Warmup)
Chain 3 Iteration: 200 / 1000 [ 20%] (Warmup)
Chain 3 Iteration: 300 / 1000 [ 30%] (Warmup)
Chain 3 Iteration: 400 / 1000 [ 40%] (Warmup)
Chain 3 Iteration: 500 / 1000 [ 50%] (Warmup)
Chain 3 Iteration: 501 / 1000 [ 50%] (Sampling)
Chain 3 Iteration: 600 / 1000 [ 60%] (Sampling)
Chain 3 Iteration: 700 / 1000 [ 70%] (Sampling)
Chain 3 Iteration: 800 / 1000 [ 80%] (Sampling)
Chain 3 Iteration: 900 / 1000 [ 90%] (Sampling)
Chain 3 Iteration: 1000 / 1000 [100%] (Sampling)
Chain 3 finished in 1.4 seconds.
Chain 4 Iteration: 1 / 1000 [ 0%] (Warmup)
Chain 4 Iteration: 100 / 1000 [ 10%] (Warmup)
Chain 4 Iteration: 200 / 1000 [ 20%] (Warmup)
Chain 4 Iteration: 300 / 1000 [ 30%] (Warmup)
Chain 4 Iteration: 400 / 1000 [ 40%] (Warmup)
Chain 4 Iteration: 500 / 1000 [ 50%] (Warmup)
Chain 4 Iteration: 501 / 1000 [ 50%] (Sampling)
Chain 4 Iteration: 600 / 1000 [ 60%] (Sampling)
Chain 4 Iteration: 700 / 1000 [ 70%] (Sampling)
Chain 4 Iteration: 800 / 1000 [ 80%] (Sampling)
Chain 4 Iteration: 900 / 1000 [ 90%] (Sampling)
Chain 4 Iteration: 1000 / 1000 [100%] (Sampling)
Chain 4 finished in 1.3 seconds.
All 4 chains finished successfully.
Mean chain execution time: 1.3 seconds.
Total execution time: 5.8 seconds.
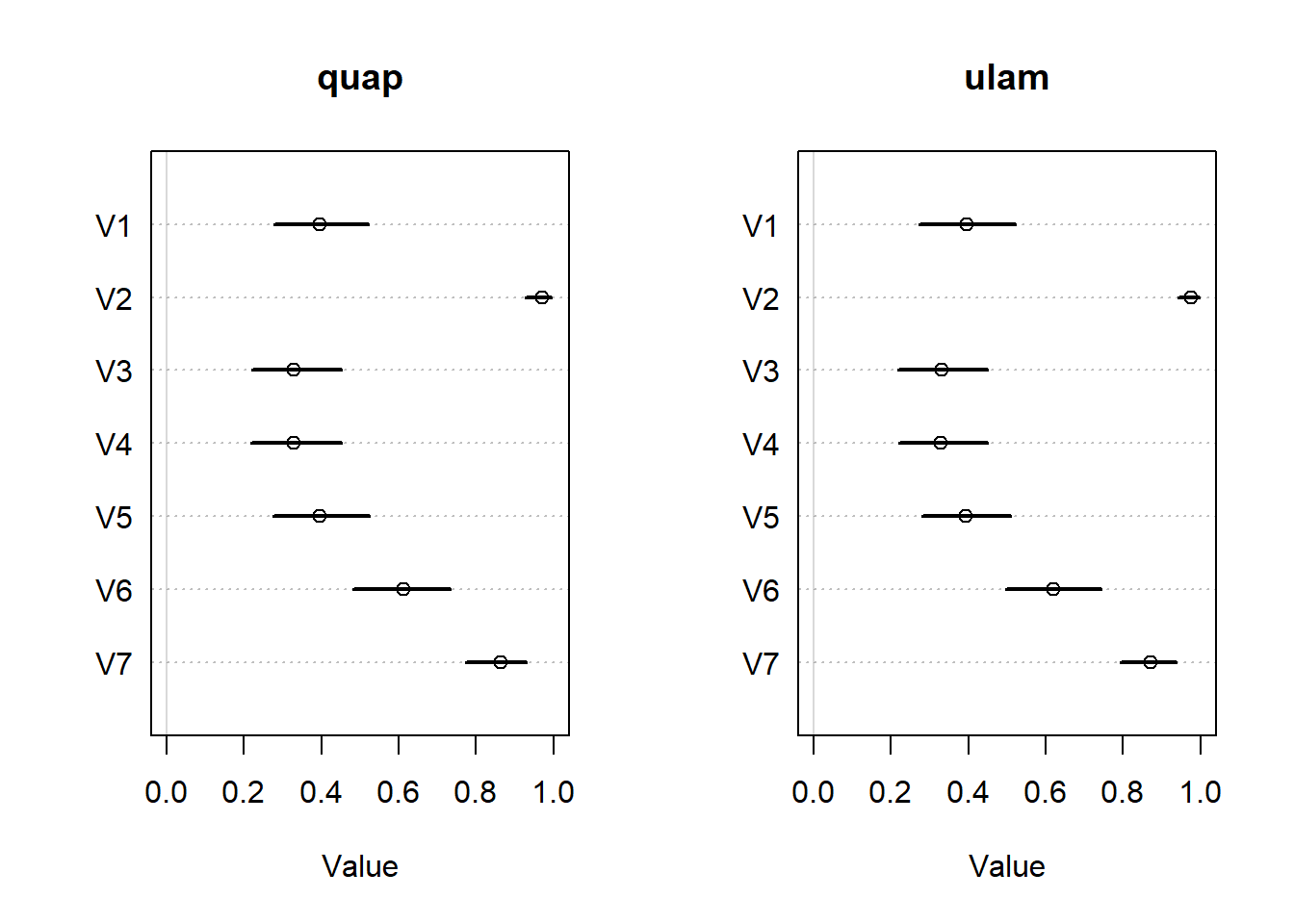
And we’ll compare the predictions of the actor effects between both models.
<- rethinking:: extract.samples (m11.4 _quap)<- rethinking:: extract.samples (m11.4 _ulam)<- rethinking:: inv_logit (post_quap$ a)<- rethinking:: inv_logit (post_ulam$ a)layout (matrix (1 : 2 , nrow = 1 ))plot (:: precis (as.data.frame (pl_quap)),xlim = c (0 , 1 ),main = "quap" plot (:: precis (as.data.frame (pl_ulam)),xlim = c (0 , 1 ),main = "ulam"
OK, those posteriors look exactly the same, so we better check the next posterior plot that’s shown in the chapter.
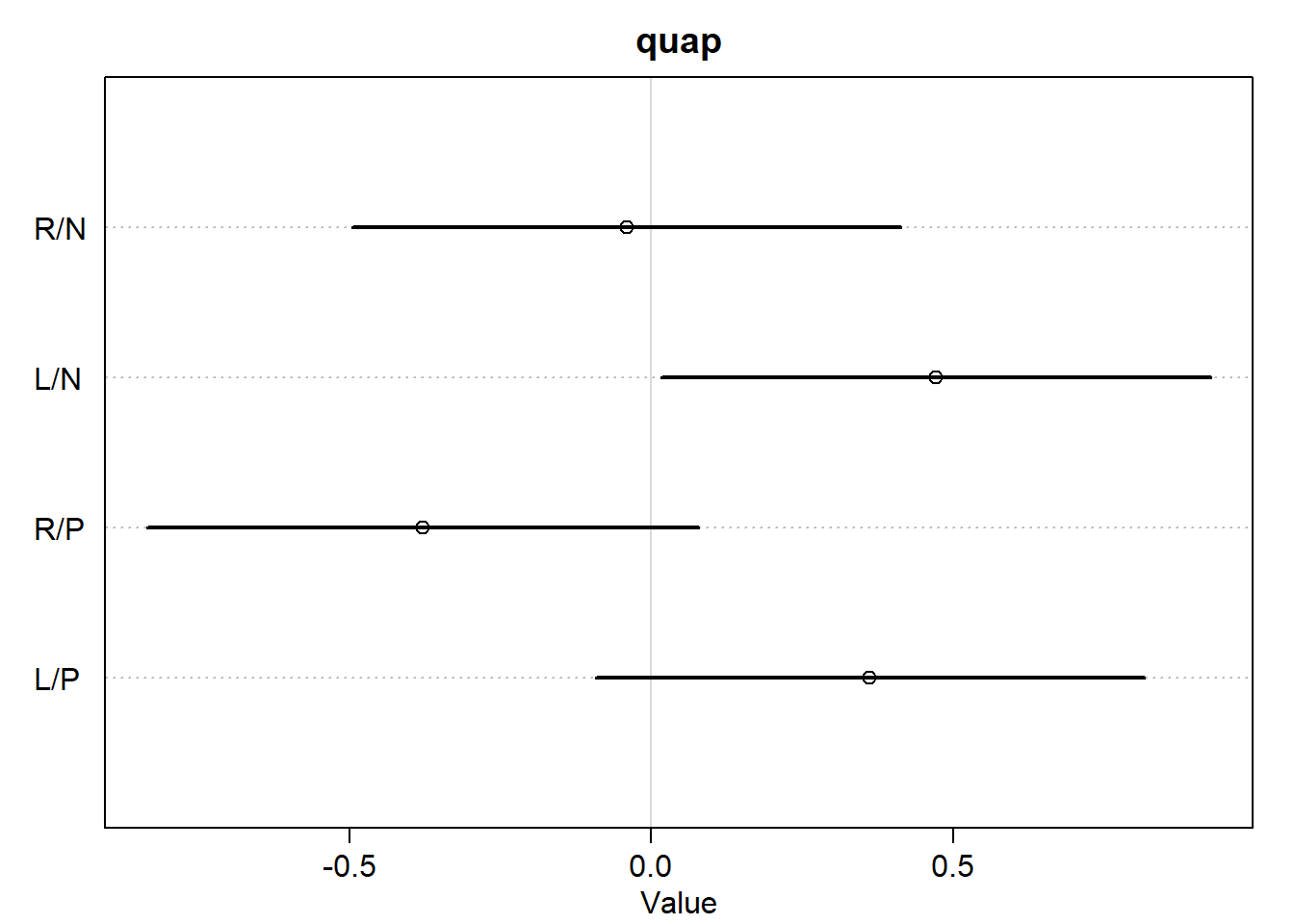
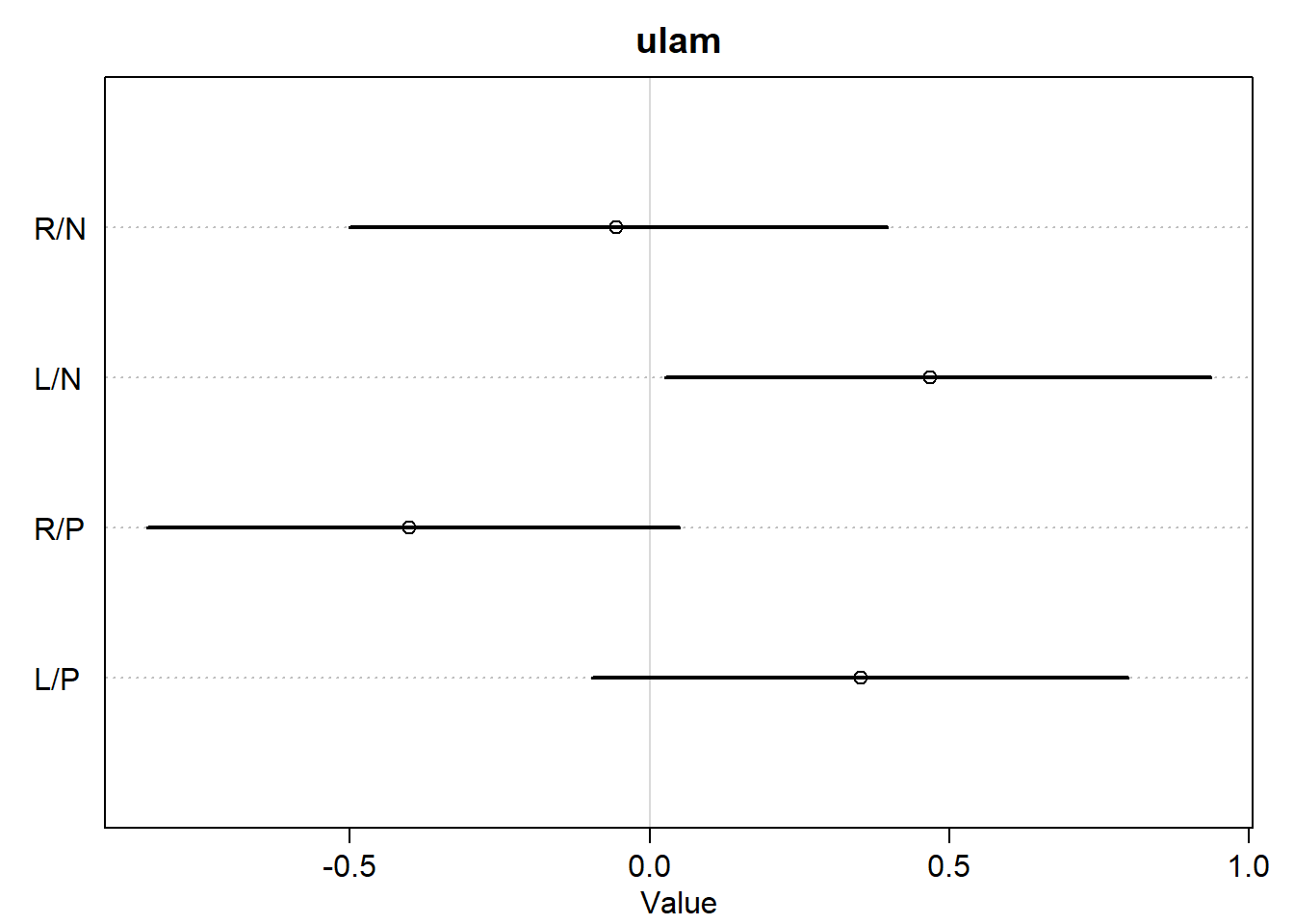
<- c ("R/N" , "L/N" , "R/P" , "L/P" )plot (:: precis (m11.4 _quap, depth = 2 , pars = "b" ),labels = labs,main = "quap" plot (:: precis (m11.4 _ulam, depth = 2 , pars = "b" ),labels = labs,main = "ulam"
OK, there are a few tiny differences, but the two models still look almost exactly the same for practical purposes. Let’s make the contrast plot just to be safe.
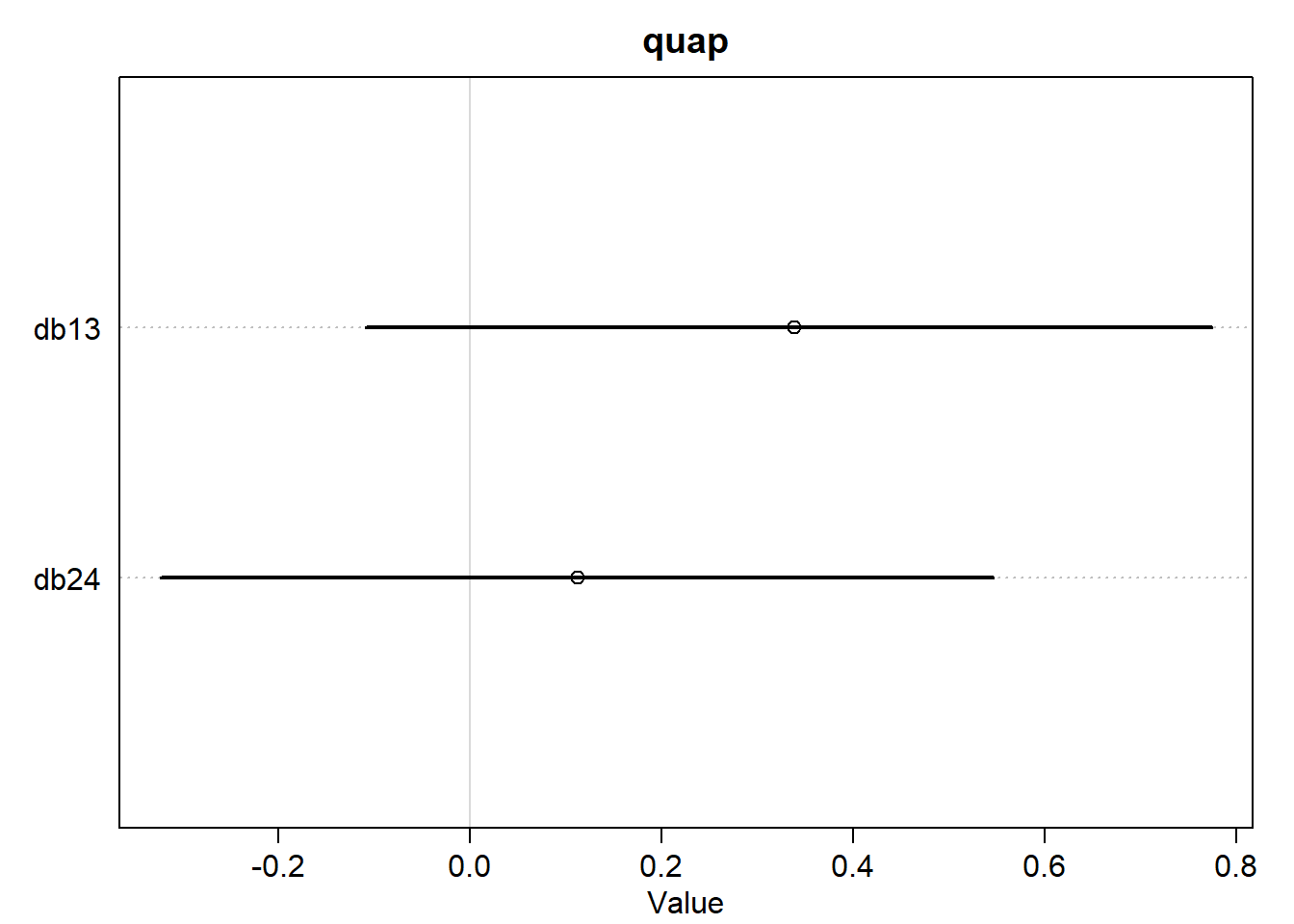
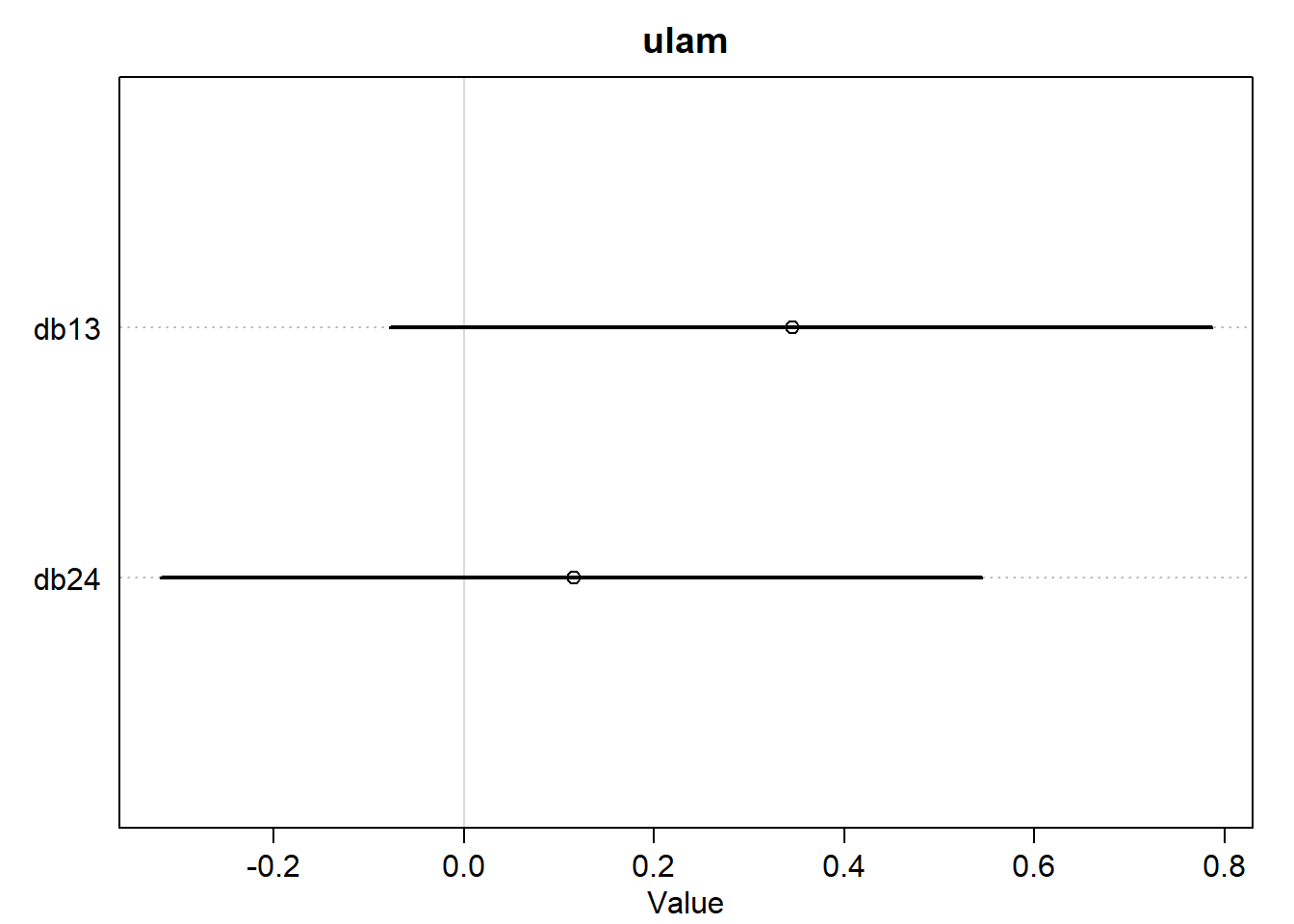
<- list (db13 = post_quap$ b[,1 ] - post_quap$ b[,3 ],db24 = post_quap$ b[,2 ] - post_quap$ b[,4 ]<- list (db13 = post_ulam$ b[,1 ] - post_ulam$ b[,3 ],db24 = post_ulam$ b[,2 ] - post_ulam$ b[,4 ]plot (:: precis (diffs_quap),main = "quap" plot (:: precis (diffs_ulam),main = "ulam"
OK, those also look exactly the same. The way the question is wording is sort of leading and I was expecting to see a difference. But I guess we better just plot the exact parameter estimates.
Show plot code (long-ish)
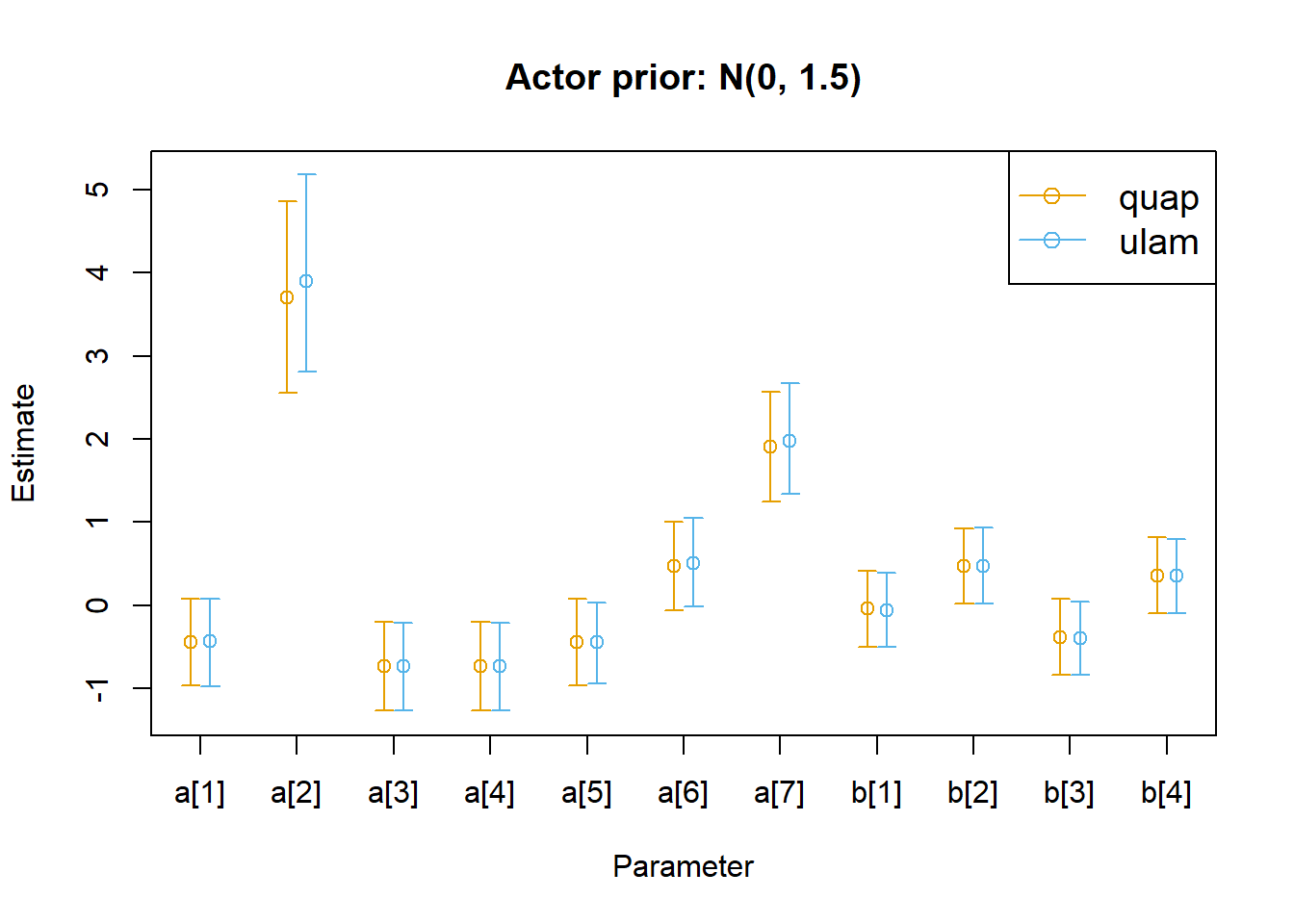
<- rethinking:: precis (m11.4 _quap, depth = 2 ) |> as.data.frame ()<- rethinking:: precis (m11.4 _ulam, depth = 2 ) |> as.data.frame ()<- nrow (parms_quap)<- c (0.9 , n + 0.1 )<- c (min (min (parms_quap$ ` 5.5% ` , parms_ulam$ ` 5.5% ` )),max (max (parms_quap$ ` 94.5% ` , parms_ulam$ ` 94.5% ` ))|> round (1 )<- 0.1 # dodge factor # Plot setup layout (1 )plot (NULL , NULL ,xlim = xrange,ylim = yrange,xlab = "Parameter" ,ylab = "Estimate" ,xaxt = "n" ,main = "Actor prior: N(0, 1.5)" axis (1 , at = 1 : n, labels = rownames (parms_quap))legend ("topright" ,legend = c ("quap" , "ulam" ),col = c ("#e69f00" , "#56b4e9" ),pch = 1 ,lty = 1 ,cex = 1.2 # quap estimates points (x = 1 : n - d,y = parms_quap$ mean,col = "#e69f00" arrows (x0 = 1 : n - d,,y0 = parms_quap$ ` 5.5% ` ,x = 1 : n - d,y = parms_quap$ ` 94.5% ` ,length = 0.05 ,angle = 90 ,code = 3 ,col = "#e69f00" # ulam estimates points (x = 1 : n + d,y = parms_ulam$ mean,col = "#56b4e9" arrows (x0 = 1 : n + d,,y0 = parms_ulam$ ` 5.5% ` ,x = 1 : n + d,y = parms_ulam$ ` 94.5% ` ,length = 0.05 ,angle = 90 ,code = 3 ,col = "#56b4e9"
Yeah, the parameter estimates are almost all identical. Maybe that was the point, let’s try relaxing the priors on the actor intercepts to see if that changes the estimates.
<- alist (~ dbinom (1 , p),logit (p) <- a[actor] + b[treatment],~ dnorm (0 , 10 ),~ dnorm (0 , 0.5 ).4 _r_quap <- rethinking:: quap (flist = chimp_model_r,data = dat_list.4 _r_ulam <- rethinking:: ulam (flist = chimp_model_r,data = dat_list,chains = 4 , cores = 4 ,log_lik = TRUE
In file included from stan/src/stan/model/model_header.hpp:5:
stan/src/stan/model/model_base_crtp.hpp:205:8: warning: 'void stan::model::model_base_crtp<M>::write_array(stan::rng_t&, std::vector<double>&, std::vector<int>&, std::vector<double>&, bool, bool, std::ostream*) const [with M = ulam_cmdstanr_6d6480bb4a0ed7b052bc83ca092e6e10_model_namespace::ulam_cmdstanr_6d6480bb4a0ed7b052bc83ca092e6e10_model; stan::rng_t = boost::random::mixmax_engine<17, 36, 0>; std::ostream = std::basic_ostream<char>]' was hidden [-Woverloaded-virtual=]
205 | void write_array(stan::rng_t& rng, std::vector<double>& theta,
| ^~~~~~~~~~~
C:/Users/Zane/AppData/Local/Temp/RtmpSCWF6a/model-305c2c305688.hpp:492: note: by 'ulam_cmdstanr_6d6480bb4a0ed7b052bc83ca092e6e10_model_namespace::ulam_cmdstanr_6d6480bb4a0ed7b052bc83ca092e6e10_model::write_array'
492 | write_array(RNG& base_rng, std::vector<double>& params_r, std::vector<int>&
stan/src/stan/model/model_base_crtp.hpp:136:8: warning: 'void stan::model::model_base_crtp<M>::write_array(stan::rng_t&, Eigen::VectorXd&, Eigen::VectorXd&, bool, bool, std::ostream*) const [with M = ulam_cmdstanr_6d6480bb4a0ed7b052bc83ca092e6e10_model_namespace::ulam_cmdstanr_6d6480bb4a0ed7b052bc83ca092e6e10_model; stan::rng_t = boost::random::mixmax_engine<17, 36, 0>; Eigen::VectorXd = Eigen::Matrix<double, -1, 1>; std::ostream = std::basic_ostream<char>]' was hidden [-Woverloaded-virtual=]
136 | void write_array(stan::rng_t& rng, Eigen::VectorXd& theta,
| ^~~~~~~~~~~
C:/Users/Zane/AppData/Local/Temp/RtmpSCWF6a/model-305c2c305688.hpp:492: note: by 'ulam_cmdstanr_6d6480bb4a0ed7b052bc83ca092e6e10_model_namespace::ulam_cmdstanr_6d6480bb4a0ed7b052bc83ca092e6e10_model::write_array'
492 | write_array(RNG& base_rng, std::vector<double>& params_r, std::vector<int>&
Running MCMC with 4 parallel chains, with 1 thread(s) per chain...
Chain 1 Iteration: 1 / 1000 [ 0%] (Warmup)
Chain 2 Iteration: 1 / 1000 [ 0%] (Warmup)
Chain 3 Iteration: 1 / 1000 [ 0%] (Warmup)
Chain 4 Iteration: 1 / 1000 [ 0%] (Warmup)
Chain 1 Iteration: 100 / 1000 [ 10%] (Warmup)
Chain 2 Iteration: 100 / 1000 [ 10%] (Warmup)
Chain 3 Iteration: 100 / 1000 [ 10%] (Warmup)
Chain 4 Iteration: 100 / 1000 [ 10%] (Warmup)
Chain 1 Iteration: 200 / 1000 [ 20%] (Warmup)
Chain 2 Iteration: 200 / 1000 [ 20%] (Warmup)
Chain 3 Iteration: 200 / 1000 [ 20%] (Warmup)
Chain 4 Iteration: 200 / 1000 [ 20%] (Warmup)
Chain 1 Iteration: 300 / 1000 [ 30%] (Warmup)
Chain 2 Iteration: 300 / 1000 [ 30%] (Warmup)
Chain 3 Iteration: 300 / 1000 [ 30%] (Warmup)
Chain 4 Iteration: 300 / 1000 [ 30%] (Warmup)
Chain 1 Iteration: 400 / 1000 [ 40%] (Warmup)
Chain 2 Iteration: 400 / 1000 [ 40%] (Warmup)
Chain 3 Iteration: 400 / 1000 [ 40%] (Warmup)
Chain 4 Iteration: 400 / 1000 [ 40%] (Warmup)
Chain 2 Iteration: 500 / 1000 [ 50%] (Warmup)
Chain 1 Iteration: 500 / 1000 [ 50%] (Warmup)
Chain 2 Iteration: 501 / 1000 [ 50%] (Sampling)
Chain 3 Iteration: 500 / 1000 [ 50%] (Warmup)
Chain 4 Iteration: 500 / 1000 [ 50%] (Warmup)
Chain 1 Iteration: 501 / 1000 [ 50%] (Sampling)
Chain 1 Iteration: 600 / 1000 [ 60%] (Sampling)
Chain 2 Iteration: 600 / 1000 [ 60%] (Sampling)
Chain 3 Iteration: 501 / 1000 [ 50%] (Sampling)
Chain 3 Iteration: 600 / 1000 [ 60%] (Sampling)
Chain 4 Iteration: 501 / 1000 [ 50%] (Sampling)
Chain 4 Iteration: 600 / 1000 [ 60%] (Sampling)
Chain 1 Iteration: 700 / 1000 [ 70%] (Sampling)
Chain 2 Iteration: 700 / 1000 [ 70%] (Sampling)
Chain 3 Iteration: 700 / 1000 [ 70%] (Sampling)
Chain 2 Iteration: 800 / 1000 [ 80%] (Sampling)
Chain 4 Iteration: 700 / 1000 [ 70%] (Sampling)
Chain 1 Iteration: 800 / 1000 [ 80%] (Sampling)
Chain 3 Iteration: 800 / 1000 [ 80%] (Sampling)
Chain 1 Iteration: 900 / 1000 [ 90%] (Sampling)
Chain 2 Iteration: 900 / 1000 [ 90%] (Sampling)
Chain 3 Iteration: 900 / 1000 [ 90%] (Sampling)
Chain 4 Iteration: 800 / 1000 [ 80%] (Sampling)
Chain 1 Iteration: 1000 / 1000 [100%] (Sampling)
Chain 2 Iteration: 1000 / 1000 [100%] (Sampling)
Chain 3 Iteration: 1000 / 1000 [100%] (Sampling)
Chain 4 Iteration: 900 / 1000 [ 90%] (Sampling)
Chain 1 finished in 1.9 seconds.
Chain 2 finished in 1.8 seconds.
Chain 3 finished in 1.8 seconds.
Chain 4 Iteration: 1000 / 1000 [100%] (Sampling)
Chain 4 finished in 2.1 seconds.
All 4 chains finished successfully.
Mean chain execution time: 1.9 seconds.
Total execution time: 2.2 seconds.
This time we’ll go straight to the parameters plot to see if there are any differences between the model fits.
Show plot code (long-ish)
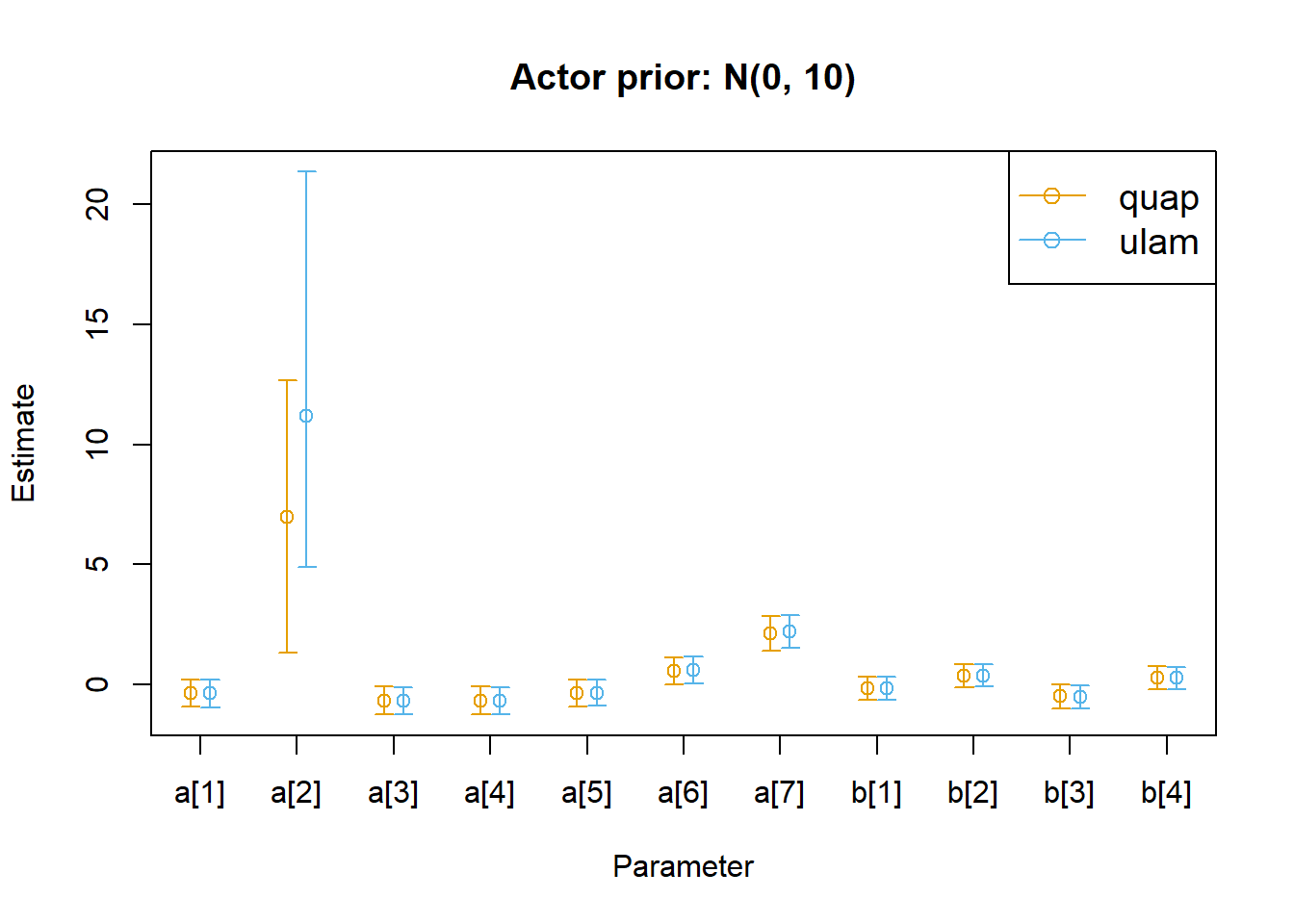
<- rethinking:: precis (m11.4 _r_quap, depth = 2 ) |> as.data.frame ()<- rethinking:: precis (m11.4 _r_ulam, depth = 2 ) |> as.data.frame ()<- nrow (parms_r_quap)<- c (0.9 , n + 0.1 )<- c (min (min (parms_r_quap$ ` 5.5% ` , parms_r_ulam$ ` 5.5% ` )),max (max (parms_r_quap$ ` 94.5% ` , parms_r_ulam$ ` 94.5% ` ))|> round (1 )<- 0.1 # dodge factor # Plot setup layout (1 )plot (NULL , NULL ,xlim = xrange,ylim = yrange,xlab = "Parameter" ,ylab = "Estimate" ,xaxt = "n" ,main = "Actor prior: N(0, 10)" axis (1 , at = 1 : n, labels = rownames (parms_r_quap))legend ("topright" ,legend = c ("quap" , "ulam" ),col = c ("#e69f00" , "#56b4e9" ),pch = 1 ,lty = 1 ,cex = 1.2 # quap estimates points (x = 1 : n - d,y = parms_r_quap$ mean,col = "#e69f00" arrows (x0 = 1 : n - d,,y0 = parms_r_quap$ ` 5.5% ` ,x = 1 : n - d,y = parms_r_quap$ ` 94.5% ` ,length = 0.05 ,angle = 90 ,code = 3 ,col = "#e69f00" # ulam estimates points (x = 1 : n + d,y = parms_r_ulam$ mean,col = "#56b4e9" arrows (x0 = 1 : n + d,,y0 = parms_r_ulam$ ` 5.5% ` ,x = 1 : n + d,y = parms_r_ulam$ ` 94.5% ` ,length = 0.05 ,angle = 90 ,code = 3 ,col = "#56b4e9"
In this case, the two algorithms still give us really similar results, but we lose the regularizing effect of our priors on the outlier case for actor 2. Our priors now presuppose a wider range of effect sizes, and actor 2 pulled the same lever in every case. So we have no data to pull the effect estimate away from the wide prior for this actor, whereas our previous weakly informative prior was providing a regularizing effect on the allowable values for this actor. But there’s no real difference between the quap and ulam fitted parameters.
I checked the solutions manual to see if maybe older versions of quap() behaved differently, but Richard McElreath seems to just have a different interpretation of “different” parameter values to me, as he interprets the values for actor 2 being different in the original model, and then being more different in the relaxed prior model. While I agree that there are numerical differences, I would argue that they aren’t meaningful in any substantial way, especially for the first model.
11M8
For this exercise, we’ll refit the island tools model but exclude Hawaii from the sample.
data (Kline, package = "rethinking" )<- Kline[Kline$ culture != "Hawaii" , ]$ P <- scale (log (d$ population))$ contact_id <- ifelse (d$ contact == "high" , 2 , 1 )<- list (T = d$ total_tools,P = d$ P,cid = d$ contact_id<- rethinking:: ulam (alist (~ dpois (lambda),log (lambda) <- a[cid] + b[cid]* P,~ dnorm (3 , 0.5 ),~ dnorm (3 , 0.2 )data = dat,chains = 4 , cores = 4 ,log_lik = TRUE
In file included from stan/src/stan/model/model_header.hpp:5:
stan/src/stan/model/model_base_crtp.hpp:205:8: warning: 'void stan::model::model_base_crtp<M>::write_array(stan::rng_t&, std::vector<double>&, std::vector<int>&, std::vector<double>&, bool, bool, std::ostream*) const [with M = ulam_cmdstanr_a7bafce69a312f89c664fe4c97927155_model_namespace::ulam_cmdstanr_a7bafce69a312f89c664fe4c97927155_model; stan::rng_t = boost::random::mixmax_engine<17, 36, 0>; std::ostream = std::basic_ostream<char>]' was hidden [-Woverloaded-virtual=]
205 | void write_array(stan::rng_t& rng, std::vector<double>& theta,
| ^~~~~~~~~~~
C:/Users/Zane/AppData/Local/Temp/RtmpSCWF6a/model-305c1a9a1953.hpp:505: note: by 'ulam_cmdstanr_a7bafce69a312f89c664fe4c97927155_model_namespace::ulam_cmdstanr_a7bafce69a312f89c664fe4c97927155_model::write_array'
505 | write_array(RNG& base_rng, std::vector<double>& params_r, std::vector<int>&
stan/src/stan/model/model_base_crtp.hpp:136:8: warning: 'void stan::model::model_base_crtp<M>::write_array(stan::rng_t&, Eigen::VectorXd&, Eigen::VectorXd&, bool, bool, std::ostream*) const [with M = ulam_cmdstanr_a7bafce69a312f89c664fe4c97927155_model_namespace::ulam_cmdstanr_a7bafce69a312f89c664fe4c97927155_model; stan::rng_t = boost::random::mixmax_engine<17, 36, 0>; Eigen::VectorXd = Eigen::Matrix<double, -1, 1>; std::ostream = std::basic_ostream<char>]' was hidden [-Woverloaded-virtual=]
136 | void write_array(stan::rng_t& rng, Eigen::VectorXd& theta,
| ^~~~~~~~~~~
C:/Users/Zane/AppData/Local/Temp/RtmpSCWF6a/model-305c1a9a1953.hpp:505: note: by 'ulam_cmdstanr_a7bafce69a312f89c664fe4c97927155_model_namespace::ulam_cmdstanr_a7bafce69a312f89c664fe4c97927155_model::write_array'
505 | write_array(RNG& base_rng, std::vector<double>& params_r, std::vector<int>&
Running MCMC with 4 parallel chains, with 1 thread(s) per chain...
Chain 1 Iteration: 1 / 1000 [ 0%] (Warmup)
Chain 1 Iteration: 100 / 1000 [ 10%] (Warmup)
Chain 1 Iteration: 200 / 1000 [ 20%] (Warmup)
Chain 1 Iteration: 300 / 1000 [ 30%] (Warmup)
Chain 1 Iteration: 400 / 1000 [ 40%] (Warmup)
Chain 1 Iteration: 500 / 1000 [ 50%] (Warmup)
Chain 1 Iteration: 501 / 1000 [ 50%] (Sampling)
Chain 1 Iteration: 600 / 1000 [ 60%] (Sampling)
Chain 1 Iteration: 700 / 1000 [ 70%] (Sampling)
Chain 1 Iteration: 800 / 1000 [ 80%] (Sampling)
Chain 1 Iteration: 900 / 1000 [ 90%] (Sampling)
Chain 1 Iteration: 1000 / 1000 [100%] (Sampling)
Chain 2 Iteration: 1 / 1000 [ 0%] (Warmup)
Chain 2 Iteration: 100 / 1000 [ 10%] (Warmup)
Chain 2 Iteration: 200 / 1000 [ 20%] (Warmup)
Chain 2 Iteration: 300 / 1000 [ 30%] (Warmup)
Chain 2 Iteration: 400 / 1000 [ 40%] (Warmup)
Chain 2 Iteration: 500 / 1000 [ 50%] (Warmup)
Chain 2 Iteration: 501 / 1000 [ 50%] (Sampling)
Chain 2 Iteration: 600 / 1000 [ 60%] (Sampling)
Chain 2 Iteration: 700 / 1000 [ 70%] (Sampling)
Chain 2 Iteration: 800 / 1000 [ 80%] (Sampling)
Chain 2 Iteration: 900 / 1000 [ 90%] (Sampling)
Chain 2 Iteration: 1000 / 1000 [100%] (Sampling)
Chain 3 Iteration: 1 / 1000 [ 0%] (Warmup)
Chain 3 Iteration: 100 / 1000 [ 10%] (Warmup)
Chain 3 Iteration: 200 / 1000 [ 20%] (Warmup)
Chain 3 Iteration: 300 / 1000 [ 30%] (Warmup)
Chain 3 Iteration: 400 / 1000 [ 40%] (Warmup)
Chain 3 Iteration: 500 / 1000 [ 50%] (Warmup)
Chain 3 Iteration: 501 / 1000 [ 50%] (Sampling)
Chain 3 Iteration: 600 / 1000 [ 60%] (Sampling)
Chain 3 Iteration: 700 / 1000 [ 70%] (Sampling)
Chain 3 Iteration: 800 / 1000 [ 80%] (Sampling)
Chain 3 Iteration: 900 / 1000 [ 90%] (Sampling)
Chain 3 Iteration: 1000 / 1000 [100%] (Sampling)
Chain 4 Iteration: 1 / 1000 [ 0%] (Warmup)
Chain 4 Iteration: 100 / 1000 [ 10%] (Warmup)
Chain 4 Iteration: 200 / 1000 [ 20%] (Warmup)
Chain 4 Iteration: 300 / 1000 [ 30%] (Warmup)
Chain 4 Iteration: 400 / 1000 [ 40%] (Warmup)
Chain 4 Iteration: 500 / 1000 [ 50%] (Warmup)
Chain 4 Iteration: 501 / 1000 [ 50%] (Sampling)
Chain 4 Iteration: 600 / 1000 [ 60%] (Sampling)
Chain 4 Iteration: 700 / 1000 [ 70%] (Sampling)
Chain 4 Iteration: 800 / 1000 [ 80%] (Sampling)
Chain 4 Iteration: 900 / 1000 [ 90%] (Sampling)
Chain 4 Iteration: 1000 / 1000 [100%] (Sampling)
Chain 1 finished in 0.1 seconds.
Chain 2 finished in 0.1 seconds.
Chain 3 finished in 0.0 seconds.
Chain 4 finished in 0.0 seconds.
All 4 chains finished successfully.
Mean chain execution time: 0.1 seconds.
Total execution time: 0.3 seconds.
Let’s get the predicts and make a plot.
Show code (long)
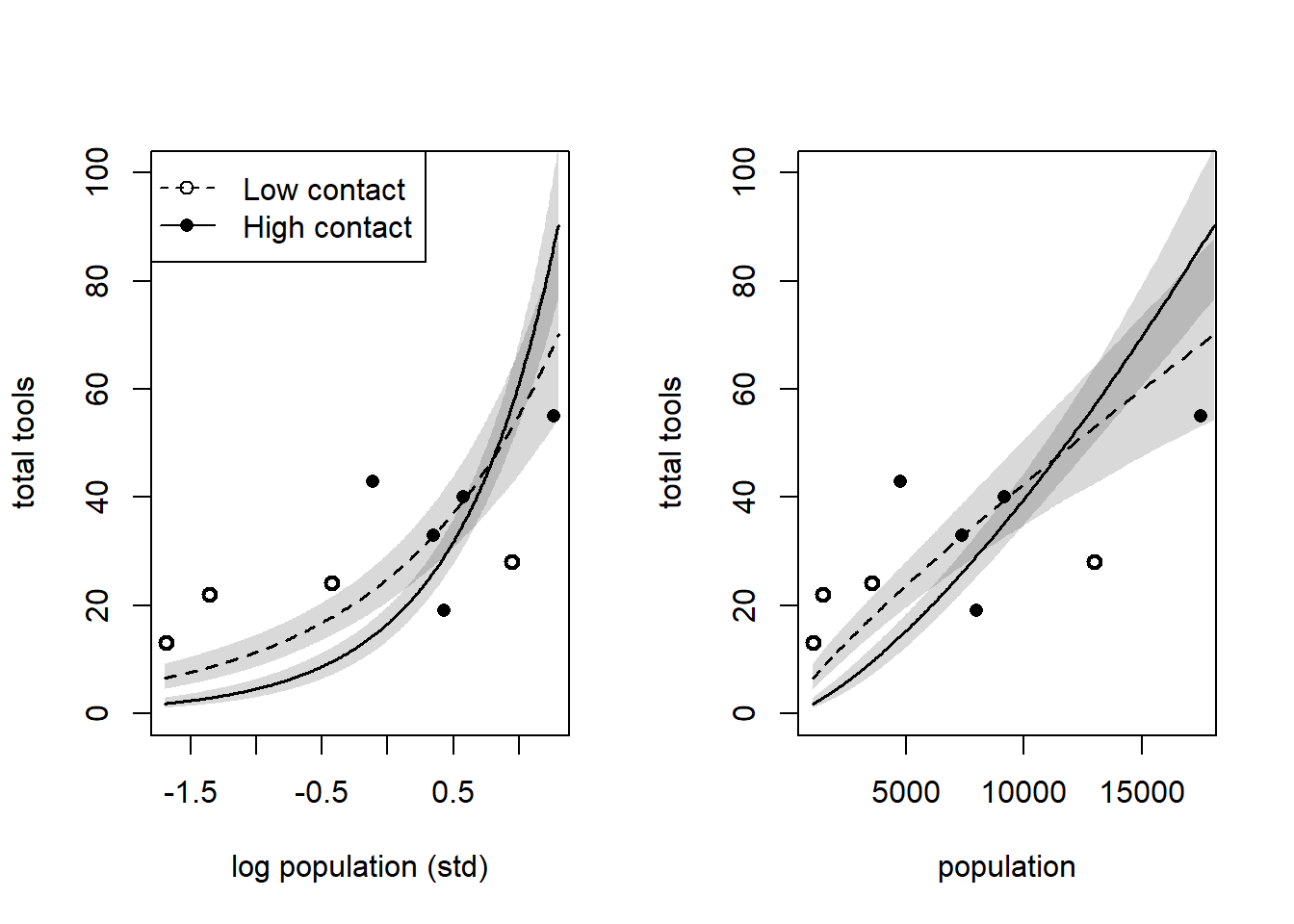
layout (matrix (1 : 2 , nrow = 1 ))plot ($ P, dat$ T,xlab = "log population (std)" ,ylab = "total tools" ,pch = ifelse (dat$ cid == 1 , 1 , 16 ),lwd = 2 ,ylim = c (0 , 100 )<- seq (from = - 1.7 , to = 1.3 , by = 0.01 )# Predictions for cid = 1 <- rethinking:: link (m_11m8, data = data.frame (P = P_seq, cid = 1 ))<- apply (lambda, 2 , mean)<- apply (lambda, 2 , rethinking:: PI)lines (P_seq, lmu, lty = 2 , lwd = 1.5 ):: shade (lci, P_seq, xpd = TRUE )# Predictions for cid = 2 <- rethinking:: link (m_11m8, data = data.frame (P = P_seq, cid = 2 ))<- apply (lambda, 2 , mean)<- apply (lambda, 2 , rethinking:: PI)lines (P_seq, lmu, lty = 1 , lwd = 1.5 ):: shade (lci, P_seq, xpd = TRUE )legend ("topleft" ,pch = c (1 , 16 ),lty = c (2 , 1 ),legend = c ("Low contact" , "High contact" )# Natural scale population plot plot ($ population, d$ total_tools,xlab = "population" , ylab = "total tools" ,pch = ifelse (dat$ cid == 1 , 1 , 16 ),lwd = 2 ,ylim = c (0 , 100 )<- exp (P_seq * 0.94 + 8.58 )# Predictions for cid = 1 <- rethinking:: link (m_11m8, data = data.frame (P = P_seq, cid = 1 ))<- apply (lambda, 2 , mean)<- apply (lambda, 2 , rethinking:: PI)lines (pop_seq, lmu, lty = 2 , lwd = 1.5 ):: shade (lci, pop_seq, xpd = TRUE )# Predictions for cid = 2 <- rethinking:: link (m_11m8, data = data.frame (P = P_seq, cid = 2 ))<- apply (lambda, 2 , mean)<- apply (lambda, 2 , rethinking:: PI)lines (pop_seq, lmu, lty = 1 , lwd = 1.5 ):: shade (lci, pop_seq, xpd = TRUE )
Interestingly, without Hawaii in the model, the model now predicts that the number of tools will grow faster, and we don’t see diminishing returns of population as strongly as we do in the model with Hawaii. We still see the crossover effect though, indicating that the model predicts that past a certain population threshold, the rate of acquiring tools increases faster for high contact populations than for low contact populations. Interestingly, our model without Hawaii also implies that high contact populations acquire tools slower than low contact populations for low population sizes, which is the opposite of what theory and the model with Hawaii told us. But that’s likely because the low-contact populations all have smaller population sizes other than Hawaii and Manus, while there are no comparable high-contact populations with the smallest population sizes.
So Hawaii is influential on our model, but that seems to be a good thing – as Hawaii has a population an order of magnitude higher than Tonga (the culture with the second largest population) but only 20 more tools than Tonga, it helps to limit the model estimation of the number of tools acquired as the population grows.
11H1
For this problem, we want to compare the simpler chimpanzee lever models to the model with unique actor intercepts.
First I have to do the data processing again, cause I overwrote the data d in the Kline data problem, which made me really think I should use unique variable names instead of just copying d from the textbook. But I’m going to do that again. Then we’ll fit the three models to compare (m11.2 and m11.3 are the same other than the choice of priors for the treatment effect).
data (chimpanzees, package = "rethinking" )<- chimpanzees$ treatment <- 1 + d$ prosoc_left + 2 * d$ condition<- list (pulled_left = d$ pulled_left,actor = d$ actor,treatment = as.integer (d$ treatment).1 <- rethinking:: ulam (flist = alist (~ dbinom (1 , p),logit (p) <- a,~ dnorm (0 , 10 )data = dat_list,chains = 4 , cores = 4 ,log_lik = TRUE
In file included from stan/src/stan/model/model_header.hpp:5:
stan/src/stan/model/model_base_crtp.hpp:205:8: warning: 'void stan::model::model_base_crtp<M>::write_array(stan::rng_t&, std::vector<double>&, std::vector<int>&, std::vector<double>&, bool, bool, std::ostream*) const [with M = ulam_cmdstanr_6381f795dc1f3858984a57023b55cf39_model_namespace::ulam_cmdstanr_6381f795dc1f3858984a57023b55cf39_model; stan::rng_t = boost::random::mixmax_engine<17, 36, 0>; std::ostream = std::basic_ostream<char>]' was hidden [-Woverloaded-virtual=]
205 | void write_array(stan::rng_t& rng, std::vector<double>& theta,
| ^~~~~~~~~~~
C:/Users/Zane/AppData/Local/Temp/RtmpSCWF6a/model-305c6c181b15.hpp:366: note: by 'ulam_cmdstanr_6381f795dc1f3858984a57023b55cf39_model_namespace::ulam_cmdstanr_6381f795dc1f3858984a57023b55cf39_model::write_array'
366 | write_array(RNG& base_rng, std::vector<double>& params_r, std::vector<int>&
stan/src/stan/model/model_base_crtp.hpp:136:8: warning: 'void stan::model::model_base_crtp<M>::write_array(stan::rng_t&, Eigen::VectorXd&, Eigen::VectorXd&, bool, bool, std::ostream*) const [with M = ulam_cmdstanr_6381f795dc1f3858984a57023b55cf39_model_namespace::ulam_cmdstanr_6381f795dc1f3858984a57023b55cf39_model; stan::rng_t = boost::random::mixmax_engine<17, 36, 0>; Eigen::VectorXd = Eigen::Matrix<double, -1, 1>; std::ostream = std::basic_ostream<char>]' was hidden [-Woverloaded-virtual=]
136 | void write_array(stan::rng_t& rng, Eigen::VectorXd& theta,
| ^~~~~~~~~~~
C:/Users/Zane/AppData/Local/Temp/RtmpSCWF6a/model-305c6c181b15.hpp:366: note: by 'ulam_cmdstanr_6381f795dc1f3858984a57023b55cf39_model_namespace::ulam_cmdstanr_6381f795dc1f3858984a57023b55cf39_model::write_array'
366 | write_array(RNG& base_rng, std::vector<double>& params_r, std::vector<int>&
Running MCMC with 4 parallel chains, with 1 thread(s) per chain...
Chain 1 Iteration: 1 / 1000 [ 0%] (Warmup)
Chain 1 Iteration: 100 / 1000 [ 10%] (Warmup)
Chain 1 Iteration: 200 / 1000 [ 20%] (Warmup)
Chain 2 Iteration: 1 / 1000 [ 0%] (Warmup)
Chain 2 Iteration: 100 / 1000 [ 10%] (Warmup)
Chain 2 Iteration: 200 / 1000 [ 20%] (Warmup)
Chain 3 Iteration: 1 / 1000 [ 0%] (Warmup)
Chain 3 Iteration: 100 / 1000 [ 10%] (Warmup)
Chain 3 Iteration: 200 / 1000 [ 20%] (Warmup)
Chain 4 Iteration: 1 / 1000 [ 0%] (Warmup)
Chain 4 Iteration: 100 / 1000 [ 10%] (Warmup)
Chain 1 Iteration: 300 / 1000 [ 30%] (Warmup)
Chain 1 Iteration: 400 / 1000 [ 40%] (Warmup)
Chain 1 Iteration: 500 / 1000 [ 50%] (Warmup)
Chain 1 Iteration: 501 / 1000 [ 50%] (Sampling)
Chain 1 Iteration: 600 / 1000 [ 60%] (Sampling)
Chain 1 Iteration: 700 / 1000 [ 70%] (Sampling)
Chain 1 Iteration: 800 / 1000 [ 80%] (Sampling)
Chain 2 Iteration: 300 / 1000 [ 30%] (Warmup)
Chain 2 Iteration: 400 / 1000 [ 40%] (Warmup)
Chain 2 Iteration: 500 / 1000 [ 50%] (Warmup)
Chain 2 Iteration: 501 / 1000 [ 50%] (Sampling)
Chain 2 Iteration: 600 / 1000 [ 60%] (Sampling)
Chain 2 Iteration: 700 / 1000 [ 70%] (Sampling)
Chain 3 Iteration: 300 / 1000 [ 30%] (Warmup)
Chain 3 Iteration: 400 / 1000 [ 40%] (Warmup)
Chain 3 Iteration: 500 / 1000 [ 50%] (Warmup)
Chain 3 Iteration: 501 / 1000 [ 50%] (Sampling)
Chain 3 Iteration: 600 / 1000 [ 60%] (Sampling)
Chain 3 Iteration: 700 / 1000 [ 70%] (Sampling)
Chain 4 Iteration: 200 / 1000 [ 20%] (Warmup)
Chain 4 Iteration: 300 / 1000 [ 30%] (Warmup)
Chain 4 Iteration: 400 / 1000 [ 40%] (Warmup)
Chain 4 Iteration: 500 / 1000 [ 50%] (Warmup)
Chain 4 Iteration: 501 / 1000 [ 50%] (Sampling)
Chain 4 Iteration: 600 / 1000 [ 60%] (Sampling)
Chain 4 Iteration: 700 / 1000 [ 70%] (Sampling)
Chain 1 Iteration: 900 / 1000 [ 90%] (Sampling)
Chain 1 Iteration: 1000 / 1000 [100%] (Sampling)
Chain 2 Iteration: 800 / 1000 [ 80%] (Sampling)
Chain 2 Iteration: 900 / 1000 [ 90%] (Sampling)
Chain 3 Iteration: 800 / 1000 [ 80%] (Sampling)
Chain 3 Iteration: 900 / 1000 [ 90%] (Sampling)
Chain 4 Iteration: 800 / 1000 [ 80%] (Sampling)
Chain 4 Iteration: 900 / 1000 [ 90%] (Sampling)
Chain 1 finished in 0.5 seconds.
Chain 2 Iteration: 1000 / 1000 [100%] (Sampling)
Chain 3 Iteration: 1000 / 1000 [100%] (Sampling)
Chain 4 Iteration: 1000 / 1000 [100%] (Sampling)
Chain 2 finished in 0.5 seconds.
Chain 3 finished in 0.5 seconds.
Chain 4 finished in 0.5 seconds.
All 4 chains finished successfully.
Mean chain execution time: 0.5 seconds.
Total execution time: 0.7 seconds.
.3 <- rethinking:: ulam (flist = alist (~ dbinom (1 , p),logit (p) <- a + b[treatment],~ dnorm (0 , 1.5 ),~ dnorm (0 , 0.5 )data = dat_list,chains = 4 , cores = 4 ,log_lik = TRUE
In file included from stan/src/stan/model/model_header.hpp:5:
stan/src/stan/model/model_base_crtp.hpp:205:8: warning: 'void stan::model::model_base_crtp<M>::write_array(stan::rng_t&, std::vector<double>&, std::vector<int>&, std::vector<double>&, bool, bool, std::ostream*) const [with M = ulam_cmdstanr_eae524465d9a8f4b995df3f74d53e0a0_model_namespace::ulam_cmdstanr_eae524465d9a8f4b995df3f74d53e0a0_model; stan::rng_t = boost::random::mixmax_engine<17, 36, 0>; std::ostream = std::basic_ostream<char>]' was hidden [-Woverloaded-virtual=]
205 | void write_array(stan::rng_t& rng, std::vector<double>& theta,
| ^~~~~~~~~~~
C:/Users/Zane/AppData/Local/Temp/RtmpSCWF6a/model-305c232e4fd6.hpp:461: note: by 'ulam_cmdstanr_eae524465d9a8f4b995df3f74d53e0a0_model_namespace::ulam_cmdstanr_eae524465d9a8f4b995df3f74d53e0a0_model::write_array'
461 | write_array(RNG& base_rng, std::vector<double>& params_r, std::vector<int>&
stan/src/stan/model/model_base_crtp.hpp:136:8: warning: 'void stan::model::model_base_crtp<M>::write_array(stan::rng_t&, Eigen::VectorXd&, Eigen::VectorXd&, bool, bool, std::ostream*) const [with M = ulam_cmdstanr_eae524465d9a8f4b995df3f74d53e0a0_model_namespace::ulam_cmdstanr_eae524465d9a8f4b995df3f74d53e0a0_model; stan::rng_t = boost::random::mixmax_engine<17, 36, 0>; Eigen::VectorXd = Eigen::Matrix<double, -1, 1>; std::ostream = std::basic_ostream<char>]' was hidden [-Woverloaded-virtual=]
136 | void write_array(stan::rng_t& rng, Eigen::VectorXd& theta,
| ^~~~~~~~~~~
C:/Users/Zane/AppData/Local/Temp/RtmpSCWF6a/model-305c232e4fd6.hpp:461: note: by 'ulam_cmdstanr_eae524465d9a8f4b995df3f74d53e0a0_model_namespace::ulam_cmdstanr_eae524465d9a8f4b995df3f74d53e0a0_model::write_array'
461 | write_array(RNG& base_rng, std::vector<double>& params_r, std::vector<int>&
Running MCMC with 4 parallel chains, with 1 thread(s) per chain...
Chain 1 Iteration: 1 / 1000 [ 0%] (Warmup)
Chain 2 Iteration: 1 / 1000 [ 0%] (Warmup)
Chain 3 Iteration: 1 / 1000 [ 0%] (Warmup)
Chain 4 Iteration: 1 / 1000 [ 0%] (Warmup)
Chain 1 Iteration: 100 / 1000 [ 10%] (Warmup)
Chain 1 Iteration: 200 / 1000 [ 20%] (Warmup)
Chain 2 Iteration: 100 / 1000 [ 10%] (Warmup)
Chain 3 Iteration: 100 / 1000 [ 10%] (Warmup)
Chain 4 Iteration: 100 / 1000 [ 10%] (Warmup)
Chain 2 Iteration: 200 / 1000 [ 20%] (Warmup)
Chain 3 Iteration: 200 / 1000 [ 20%] (Warmup)
Chain 4 Iteration: 200 / 1000 [ 20%] (Warmup)
Chain 1 Iteration: 300 / 1000 [ 30%] (Warmup)
Chain 2 Iteration: 300 / 1000 [ 30%] (Warmup)
Chain 3 Iteration: 300 / 1000 [ 30%] (Warmup)
Chain 4 Iteration: 300 / 1000 [ 30%] (Warmup)
Chain 1 Iteration: 400 / 1000 [ 40%] (Warmup)
Chain 2 Iteration: 400 / 1000 [ 40%] (Warmup)
Chain 4 Iteration: 400 / 1000 [ 40%] (Warmup)
Chain 1 Iteration: 500 / 1000 [ 50%] (Warmup)
Chain 1 Iteration: 501 / 1000 [ 50%] (Sampling)
Chain 3 Iteration: 400 / 1000 [ 40%] (Warmup)
Chain 2 Iteration: 500 / 1000 [ 50%] (Warmup)
Chain 3 Iteration: 500 / 1000 [ 50%] (Warmup)
Chain 3 Iteration: 501 / 1000 [ 50%] (Sampling)
Chain 4 Iteration: 500 / 1000 [ 50%] (Warmup)
Chain 1 Iteration: 600 / 1000 [ 60%] (Sampling)
Chain 2 Iteration: 501 / 1000 [ 50%] (Sampling)
Chain 2 Iteration: 600 / 1000 [ 60%] (Sampling)
Chain 4 Iteration: 501 / 1000 [ 50%] (Sampling)
Chain 4 Iteration: 600 / 1000 [ 60%] (Sampling)
Chain 1 Iteration: 700 / 1000 [ 70%] (Sampling)
Chain 3 Iteration: 600 / 1000 [ 60%] (Sampling)
Chain 2 Iteration: 700 / 1000 [ 70%] (Sampling)
Chain 3 Iteration: 700 / 1000 [ 70%] (Sampling)
Chain 4 Iteration: 700 / 1000 [ 70%] (Sampling)
Chain 1 Iteration: 800 / 1000 [ 80%] (Sampling)
Chain 2 Iteration: 800 / 1000 [ 80%] (Sampling)
Chain 4 Iteration: 800 / 1000 [ 80%] (Sampling)
Chain 1 Iteration: 900 / 1000 [ 90%] (Sampling)
Chain 2 Iteration: 900 / 1000 [ 90%] (Sampling)
Chain 3 Iteration: 800 / 1000 [ 80%] (Sampling)
Chain 4 Iteration: 900 / 1000 [ 90%] (Sampling)
Chain 3 Iteration: 900 / 1000 [ 90%] (Sampling)
Chain 1 Iteration: 1000 / 1000 [100%] (Sampling)
Chain 2 Iteration: 1000 / 1000 [100%] (Sampling)
Chain 4 Iteration: 1000 / 1000 [100%] (Sampling)
Chain 1 finished in 1.7 seconds.
Chain 2 finished in 1.7 seconds.
Chain 4 finished in 1.6 seconds.
Chain 3 Iteration: 1000 / 1000 [100%] (Sampling)
Chain 3 finished in 1.7 seconds.
All 4 chains finished successfully.
Mean chain execution time: 1.7 seconds.
Total execution time: 1.9 seconds.
.4 <- rethinking:: ulam (flist = alist (~ dbinom (1 , p),logit (p) <- a[actor] + b[treatment],~ dnorm (0 , 1.5 ),~ dnorm (0 , 0.5 )data = dat_list,chains = 4 , cores = 4 ,log_lik = TRUE
In file included from stan/src/stan/model/model_header.hpp:5:
stan/src/stan/model/model_base_crtp.hpp:205:8: warning: 'void stan::model::model_base_crtp<M>::write_array(stan::rng_t&, std::vector<double>&, std::vector<int>&, std::vector<double>&, bool, bool, std::ostream*) const [with M = ulam_cmdstanr_78180b32ba80da6bc9c4f0f8342b99b3_model_namespace::ulam_cmdstanr_78180b32ba80da6bc9c4f0f8342b99b3_model; stan::rng_t = boost::random::mixmax_engine<17, 36, 0>; std::ostream = std::basic_ostream<char>]' was hidden [-Woverloaded-virtual=]
205 | void write_array(stan::rng_t& rng, std::vector<double>& theta,
| ^~~~~~~~~~~
C:/Users/Zane/AppData/Local/Temp/RtmpSCWF6a/model-305c316b40f4.hpp:492: note: by 'ulam_cmdstanr_78180b32ba80da6bc9c4f0f8342b99b3_model_namespace::ulam_cmdstanr_78180b32ba80da6bc9c4f0f8342b99b3_model::write_array'
492 | write_array(RNG& base_rng, std::vector<double>& params_r, std::vector<int>&
stan/src/stan/model/model_base_crtp.hpp:136:8: warning: 'void stan::model::model_base_crtp<M>::write_array(stan::rng_t&, Eigen::VectorXd&, Eigen::VectorXd&, bool, bool, std::ostream*) const [with M = ulam_cmdstanr_78180b32ba80da6bc9c4f0f8342b99b3_model_namespace::ulam_cmdstanr_78180b32ba80da6bc9c4f0f8342b99b3_model; stan::rng_t = boost::random::mixmax_engine<17, 36, 0>; Eigen::VectorXd = Eigen::Matrix<double, -1, 1>; std::ostream = std::basic_ostream<char>]' was hidden [-Woverloaded-virtual=]
136 | void write_array(stan::rng_t& rng, Eigen::VectorXd& theta,
| ^~~~~~~~~~~
C:/Users/Zane/AppData/Local/Temp/RtmpSCWF6a/model-305c316b40f4.hpp:492: note: by 'ulam_cmdstanr_78180b32ba80da6bc9c4f0f8342b99b3_model_namespace::ulam_cmdstanr_78180b32ba80da6bc9c4f0f8342b99b3_model::write_array'
492 | write_array(RNG& base_rng, std::vector<double>& params_r, std::vector<int>&
Running MCMC with 4 parallel chains, with 1 thread(s) per chain...
Chain 1 Iteration: 1 / 1000 [ 0%] (Warmup)
Chain 2 Iteration: 1 / 1000 [ 0%] (Warmup)
Chain 3 Iteration: 1 / 1000 [ 0%] (Warmup)
Chain 4 Iteration: 1 / 1000 [ 0%] (Warmup)
Chain 1 Iteration: 100 / 1000 [ 10%] (Warmup)
Chain 1 Iteration: 200 / 1000 [ 20%] (Warmup)
Chain 2 Iteration: 100 / 1000 [ 10%] (Warmup)
Chain 2 Iteration: 200 / 1000 [ 20%] (Warmup)
Chain 3 Iteration: 100 / 1000 [ 10%] (Warmup)
Chain 4 Iteration: 100 / 1000 [ 10%] (Warmup)
Chain 4 Iteration: 200 / 1000 [ 20%] (Warmup)
Chain 2 Iteration: 300 / 1000 [ 30%] (Warmup)
Chain 3 Iteration: 200 / 1000 [ 20%] (Warmup)
Chain 1 Iteration: 300 / 1000 [ 30%] (Warmup)
Chain 3 Iteration: 300 / 1000 [ 30%] (Warmup)
Chain 4 Iteration: 300 / 1000 [ 30%] (Warmup)
Chain 1 Iteration: 400 / 1000 [ 40%] (Warmup)
Chain 2 Iteration: 400 / 1000 [ 40%] (Warmup)
Chain 3 Iteration: 400 / 1000 [ 40%] (Warmup)
Chain 4 Iteration: 400 / 1000 [ 40%] (Warmup)
Chain 1 Iteration: 500 / 1000 [ 50%] (Warmup)
Chain 2 Iteration: 500 / 1000 [ 50%] (Warmup)
Chain 2 Iteration: 501 / 1000 [ 50%] (Sampling)
Chain 3 Iteration: 500 / 1000 [ 50%] (Warmup)
Chain 3 Iteration: 501 / 1000 [ 50%] (Sampling)
Chain 4 Iteration: 500 / 1000 [ 50%] (Warmup)
Chain 4 Iteration: 501 / 1000 [ 50%] (Sampling)
Chain 1 Iteration: 501 / 1000 [ 50%] (Sampling)
Chain 2 Iteration: 600 / 1000 [ 60%] (Sampling)
Chain 4 Iteration: 600 / 1000 [ 60%] (Sampling)
Chain 1 Iteration: 600 / 1000 [ 60%] (Sampling)
Chain 3 Iteration: 600 / 1000 [ 60%] (Sampling)
Chain 1 Iteration: 700 / 1000 [ 70%] (Sampling)
Chain 2 Iteration: 700 / 1000 [ 70%] (Sampling)
Chain 3 Iteration: 700 / 1000 [ 70%] (Sampling)
Chain 4 Iteration: 700 / 1000 [ 70%] (Sampling)
Chain 1 Iteration: 800 / 1000 [ 80%] (Sampling)
Chain 2 Iteration: 800 / 1000 [ 80%] (Sampling)
Chain 4 Iteration: 800 / 1000 [ 80%] (Sampling)
Chain 1 Iteration: 900 / 1000 [ 90%] (Sampling)
Chain 2 Iteration: 900 / 1000 [ 90%] (Sampling)
Chain 3 Iteration: 800 / 1000 [ 80%] (Sampling)
Chain 4 Iteration: 900 / 1000 [ 90%] (Sampling)
Chain 3 Iteration: 900 / 1000 [ 90%] (Sampling)
Chain 4 Iteration: 1000 / 1000 [100%] (Sampling)
Chain 4 finished in 1.4 seconds.
Chain 1 Iteration: 1000 / 1000 [100%] (Sampling)
Chain 2 Iteration: 1000 / 1000 [100%] (Sampling)
Chain 1 finished in 1.5 seconds.
Chain 2 finished in 1.5 seconds.
Chain 3 Iteration: 1000 / 1000 [100%] (Sampling)
Chain 3 finished in 1.6 seconds.
All 4 chains finished successfully.
Mean chain execution time: 1.5 seconds.
Total execution time: 1.7 seconds.
.5 <- rethinking:: ulam (flist = alist (~ dbinom (1 , p),logit (p) <- a[actor],~ dnorm (0 , 1.5 )data = dat_list,chains = 4 , cores = 4 ,log_lik = TRUE
In file included from stan/src/stan/model/model_header.hpp:5:
stan/src/stan/model/model_base_crtp.hpp:205:8: warning: 'void stan::model::model_base_crtp<M>::write_array(stan::rng_t&, std::vector<double>&, std::vector<int>&, std::vector<double>&, bool, bool, std::ostream*) const [with M = ulam_cmdstanr_3db5f73fee2854c436e38eab75da6b9b_model_namespace::ulam_cmdstanr_3db5f73fee2854c436e38eab75da6b9b_model; stan::rng_t = boost::random::mixmax_engine<17, 36, 0>; std::ostream = std::basic_ostream<char>]' was hidden [-Woverloaded-virtual=]
205 | void write_array(stan::rng_t& rng, std::vector<double>& theta,
| ^~~~~~~~~~~
C:/Users/Zane/AppData/Local/Temp/RtmpSCWF6a/model-305c7c6a7199.hpp:432: note: by 'ulam_cmdstanr_3db5f73fee2854c436e38eab75da6b9b_model_namespace::ulam_cmdstanr_3db5f73fee2854c436e38eab75da6b9b_model::write_array'
432 | write_array(RNG& base_rng, std::vector<double>& params_r, std::vector<int>&
stan/src/stan/model/model_base_crtp.hpp:136:8: warning: 'void stan::model::model_base_crtp<M>::write_array(stan::rng_t&, Eigen::VectorXd&, Eigen::VectorXd&, bool, bool, std::ostream*) const [with M = ulam_cmdstanr_3db5f73fee2854c436e38eab75da6b9b_model_namespace::ulam_cmdstanr_3db5f73fee2854c436e38eab75da6b9b_model; stan::rng_t = boost::random::mixmax_engine<17, 36, 0>; Eigen::VectorXd = Eigen::Matrix<double, -1, 1>; std::ostream = std::basic_ostream<char>]' was hidden [-Woverloaded-virtual=]
136 | void write_array(stan::rng_t& rng, Eigen::VectorXd& theta,
| ^~~~~~~~~~~
C:/Users/Zane/AppData/Local/Temp/RtmpSCWF6a/model-305c7c6a7199.hpp:432: note: by 'ulam_cmdstanr_3db5f73fee2854c436e38eab75da6b9b_model_namespace::ulam_cmdstanr_3db5f73fee2854c436e38eab75da6b9b_model::write_array'
432 | write_array(RNG& base_rng, std::vector<double>& params_r, std::vector<int>&
Running MCMC with 4 parallel chains, with 1 thread(s) per chain...
Chain 1 Iteration: 1 / 1000 [ 0%] (Warmup)
Chain 2 Iteration: 1 / 1000 [ 0%] (Warmup)
Chain 3 Iteration: 1 / 1000 [ 0%] (Warmup)
Chain 4 Iteration: 1 / 1000 [ 0%] (Warmup)
Chain 1 Iteration: 100 / 1000 [ 10%] (Warmup)
Chain 1 Iteration: 200 / 1000 [ 20%] (Warmup)
Chain 2 Iteration: 100 / 1000 [ 10%] (Warmup)
Chain 2 Iteration: 200 / 1000 [ 20%] (Warmup)
Chain 3 Iteration: 100 / 1000 [ 10%] (Warmup)
Chain 3 Iteration: 200 / 1000 [ 20%] (Warmup)
Chain 4 Iteration: 100 / 1000 [ 10%] (Warmup)
Chain 4 Iteration: 200 / 1000 [ 20%] (Warmup)
Chain 1 Iteration: 300 / 1000 [ 30%] (Warmup)
Chain 2 Iteration: 300 / 1000 [ 30%] (Warmup)
Chain 3 Iteration: 300 / 1000 [ 30%] (Warmup)
Chain 4 Iteration: 300 / 1000 [ 30%] (Warmup)
Chain 1 Iteration: 400 / 1000 [ 40%] (Warmup)
Chain 2 Iteration: 400 / 1000 [ 40%] (Warmup)
Chain 3 Iteration: 400 / 1000 [ 40%] (Warmup)
Chain 4 Iteration: 400 / 1000 [ 40%] (Warmup)
Chain 1 Iteration: 500 / 1000 [ 50%] (Warmup)
Chain 1 Iteration: 501 / 1000 [ 50%] (Sampling)
Chain 2 Iteration: 500 / 1000 [ 50%] (Warmup)
Chain 2 Iteration: 501 / 1000 [ 50%] (Sampling)
Chain 3 Iteration: 500 / 1000 [ 50%] (Warmup)
Chain 3 Iteration: 501 / 1000 [ 50%] (Sampling)
Chain 4 Iteration: 500 / 1000 [ 50%] (Warmup)
Chain 4 Iteration: 501 / 1000 [ 50%] (Sampling)
Chain 1 Iteration: 600 / 1000 [ 60%] (Sampling)
Chain 3 Iteration: 600 / 1000 [ 60%] (Sampling)
Chain 4 Iteration: 600 / 1000 [ 60%] (Sampling)
Chain 1 Iteration: 700 / 1000 [ 70%] (Sampling)
Chain 2 Iteration: 600 / 1000 [ 60%] (Sampling)
Chain 1 Iteration: 800 / 1000 [ 80%] (Sampling)
Chain 2 Iteration: 700 / 1000 [ 70%] (Sampling)
Chain 3 Iteration: 700 / 1000 [ 70%] (Sampling)
Chain 4 Iteration: 700 / 1000 [ 70%] (Sampling)
Chain 1 Iteration: 900 / 1000 [ 90%] (Sampling)
Chain 2 Iteration: 800 / 1000 [ 80%] (Sampling)
Chain 3 Iteration: 800 / 1000 [ 80%] (Sampling)
Chain 4 Iteration: 800 / 1000 [ 80%] (Sampling)
Chain 1 Iteration: 1000 / 1000 [100%] (Sampling)
Chain 2 Iteration: 900 / 1000 [ 90%] (Sampling)
Chain 3 Iteration: 900 / 1000 [ 90%] (Sampling)
Chain 4 Iteration: 900 / 1000 [ 90%] (Sampling)
Chain 1 finished in 1.3 seconds.
Chain 2 Iteration: 1000 / 1000 [100%] (Sampling)
Chain 3 Iteration: 1000 / 1000 [100%] (Sampling)
Chain 4 Iteration: 1000 / 1000 [100%] (Sampling)
Chain 2 finished in 1.3 seconds.
Chain 3 finished in 1.3 seconds.
Chain 4 finished in 1.3 seconds.
All 4 chains finished successfully.
Mean chain execution time: 1.3 seconds.
Total execution time: 1.4 seconds.
Now we’ll compare the models using PSIS.
:: compare (.1 , m11.3 , m11.4 ,sort = "PSIS" , func = PSIS
PSIS SE dPSIS dSE pPSIS weight
m11.4 532.4716 18.976515 0.0000 NA 8.593902 1.000000e+00
m11.3 682.5700 9.216209 150.0984 18.46056 3.698773 2.550081e-33
m11.1 688.0192 7.273776 155.5476 19.04362 1.037109 1.672162e-34
From the PSIS comparison, we can see that m11.4, which includes actor effects and treatment effects, is the best model (according to PSIS). That means that the actor effects are actually much more important than the treatment effects, because m11.3 includes treatment effects and is not noticebly different from the model that only includes an overall intercept.
I also fit my own new model, m11.5, which only includes an actor effect and not a treatment effect. Let’s compare that to the full model, m11.4.
:: compare (.4 , m11.5 ,sort = "PSIS" , func = PSIS
PSIS SE dPSIS dSE pPSIS weight
m11.4 532.4716 18.97652 0.000000 NA 8.593902 0.98673682
m11.5 541.0905 17.90472 8.618824 6.483193 5.736835 0.01326318
The two models are essentially indistinguishable by PSIS, which sort of implies that knowing the treatment group doesn’t give us any predictive power. I wonder if this would be different if we split the treatment group up into its two constituent effects.
$ condition <- d$ condition + 1 $ prosoc_left <- d$ prosoc_left + 1 .6 <- rethinking:: ulam (flist = alist (~ dbinom (1 , p),logit (p) <- a[actor] + b[condition],~ dnorm (0 , 1.5 ),~ dnorm (0 , 1.5 )data = dat_list,chains = 4 , cores = 4 ,log_lik = TRUE
In file included from stan/src/stan/model/model_header.hpp:5:
stan/src/stan/model/model_base_crtp.hpp:205:8: warning: 'void stan::model::model_base_crtp<M>::write_array(stan::rng_t&, std::vector<double>&, std::vector<int>&, std::vector<double>&, bool, bool, std::ostream*) const [with M = ulam_cmdstanr_3edff36c47e534dceb57f0a0e4b40178_model_namespace::ulam_cmdstanr_3edff36c47e534dceb57f0a0e4b40178_model; stan::rng_t = boost::random::mixmax_engine<17, 36, 0>; std::ostream = std::basic_ostream<char>]' was hidden [-Woverloaded-virtual=]
205 | void write_array(stan::rng_t& rng, std::vector<double>& theta,
| ^~~~~~~~~~~
C:/Users/Zane/AppData/Local/Temp/RtmpSCWF6a/model-305c71be64c5.hpp:508: note: by 'ulam_cmdstanr_3edff36c47e534dceb57f0a0e4b40178_model_namespace::ulam_cmdstanr_3edff36c47e534dceb57f0a0e4b40178_model::write_array'
508 | write_array(RNG& base_rng, std::vector<double>& params_r, std::vector<int>&
stan/src/stan/model/model_base_crtp.hpp:136:8: warning: 'void stan::model::model_base_crtp<M>::write_array(stan::rng_t&, Eigen::VectorXd&, Eigen::VectorXd&, bool, bool, std::ostream*) const [with M = ulam_cmdstanr_3edff36c47e534dceb57f0a0e4b40178_model_namespace::ulam_cmdstanr_3edff36c47e534dceb57f0a0e4b40178_model; stan::rng_t = boost::random::mixmax_engine<17, 36, 0>; Eigen::VectorXd = Eigen::Matrix<double, -1, 1>; std::ostream = std::basic_ostream<char>]' was hidden [-Woverloaded-virtual=]
136 | void write_array(stan::rng_t& rng, Eigen::VectorXd& theta,
| ^~~~~~~~~~~
C:/Users/Zane/AppData/Local/Temp/RtmpSCWF6a/model-305c71be64c5.hpp:508: note: by 'ulam_cmdstanr_3edff36c47e534dceb57f0a0e4b40178_model_namespace::ulam_cmdstanr_3edff36c47e534dceb57f0a0e4b40178_model::write_array'
508 | write_array(RNG& base_rng, std::vector<double>& params_r, std::vector<int>&
Running MCMC with 4 parallel chains, with 1 thread(s) per chain...
Chain 1 Iteration: 1 / 1000 [ 0%] (Warmup)
Chain 2 Iteration: 1 / 1000 [ 0%] (Warmup)
Chain 3 Iteration: 1 / 1000 [ 0%] (Warmup)
Chain 4 Iteration: 1 / 1000 [ 0%] (Warmup)
Chain 1 Iteration: 100 / 1000 [ 10%] (Warmup)
Chain 2 Iteration: 100 / 1000 [ 10%] (Warmup)
Chain 3 Iteration: 100 / 1000 [ 10%] (Warmup)
Chain 4 Iteration: 100 / 1000 [ 10%] (Warmup)
Chain 1 Iteration: 200 / 1000 [ 20%] (Warmup)
Chain 2 Iteration: 200 / 1000 [ 20%] (Warmup)
Chain 3 Iteration: 200 / 1000 [ 20%] (Warmup)
Chain 4 Iteration: 200 / 1000 [ 20%] (Warmup)
Chain 1 Iteration: 300 / 1000 [ 30%] (Warmup)
Chain 2 Iteration: 300 / 1000 [ 30%] (Warmup)
Chain 3 Iteration: 300 / 1000 [ 30%] (Warmup)
Chain 4 Iteration: 300 / 1000 [ 30%] (Warmup)
Chain 1 Iteration: 400 / 1000 [ 40%] (Warmup)
Chain 2 Iteration: 400 / 1000 [ 40%] (Warmup)
Chain 3 Iteration: 400 / 1000 [ 40%] (Warmup)
Chain 4 Iteration: 400 / 1000 [ 40%] (Warmup)
Chain 1 Iteration: 500 / 1000 [ 50%] (Warmup)
Chain 2 Iteration: 500 / 1000 [ 50%] (Warmup)
Chain 3 Iteration: 500 / 1000 [ 50%] (Warmup)
Chain 1 Iteration: 501 / 1000 [ 50%] (Sampling)
Chain 1 Iteration: 600 / 1000 [ 60%] (Sampling)
Chain 2 Iteration: 501 / 1000 [ 50%] (Sampling)
Chain 3 Iteration: 501 / 1000 [ 50%] (Sampling)
Chain 4 Iteration: 500 / 1000 [ 50%] (Warmup)
Chain 2 Iteration: 600 / 1000 [ 60%] (Sampling)
Chain 3 Iteration: 600 / 1000 [ 60%] (Sampling)
Chain 4 Iteration: 501 / 1000 [ 50%] (Sampling)
Chain 4 Iteration: 600 / 1000 [ 60%] (Sampling)
Chain 1 Iteration: 700 / 1000 [ 70%] (Sampling)
Chain 2 Iteration: 700 / 1000 [ 70%] (Sampling)
Chain 3 Iteration: 700 / 1000 [ 70%] (Sampling)
Chain 4 Iteration: 700 / 1000 [ 70%] (Sampling)
Chain 1 Iteration: 800 / 1000 [ 80%] (Sampling)
Chain 2 Iteration: 800 / 1000 [ 80%] (Sampling)
Chain 3 Iteration: 800 / 1000 [ 80%] (Sampling)
Chain 1 Iteration: 900 / 1000 [ 90%] (Sampling)
Chain 2 Iteration: 900 / 1000 [ 90%] (Sampling)
Chain 4 Iteration: 800 / 1000 [ 80%] (Sampling)
Chain 3 Iteration: 900 / 1000 [ 90%] (Sampling)
Chain 4 Iteration: 900 / 1000 [ 90%] (Sampling)
Chain 1 Iteration: 1000 / 1000 [100%] (Sampling)
Chain 2 Iteration: 1000 / 1000 [100%] (Sampling)
Chain 1 finished in 1.9 seconds.
Chain 2 finished in 1.9 seconds.
Chain 3 Iteration: 1000 / 1000 [100%] (Sampling)
Chain 4 Iteration: 1000 / 1000 [100%] (Sampling)
Chain 3 finished in 2.0 seconds.
Chain 4 finished in 2.0 seconds.
All 4 chains finished successfully.
Mean chain execution time: 1.9 seconds.
Total execution time: 2.1 seconds.
.7 <- rethinking:: ulam (flist = alist (~ dbinom (1 , p),logit (p) <- a[actor] + b[prosoc_left],~ dnorm (0 , 1.5 ),~ dnorm (0 , 1.5 )data = dat_list,chains = 4 , cores = 4 ,log_lik = TRUE
In file included from stan/src/stan/model/model_header.hpp:5:
stan/src/stan/model/model_base_crtp.hpp:205:8: warning: 'void stan::model::model_base_crtp<M>::write_array(stan::rng_t&, std::vector<double>&, std::vector<int>&, std::vector<double>&, bool, bool, std::ostream*) const [with M = ulam_cmdstanr_790799fad754433849bd02c357aa0c90_model_namespace::ulam_cmdstanr_790799fad754433849bd02c357aa0c90_model; stan::rng_t = boost::random::mixmax_engine<17, 36, 0>; std::ostream = std::basic_ostream<char>]' was hidden [-Woverloaded-virtual=]
205 | void write_array(stan::rng_t& rng, std::vector<double>& theta,
| ^~~~~~~~~~~
C:/Users/Zane/AppData/Local/Temp/RtmpSCWF6a/model-305c2285bf.hpp:508: note: by 'ulam_cmdstanr_790799fad754433849bd02c357aa0c90_model_namespace::ulam_cmdstanr_790799fad754433849bd02c357aa0c90_model::write_array'
508 | write_array(RNG& base_rng, std::vector<double>& params_r, std::vector<int>&
stan/src/stan/model/model_base_crtp.hpp:136:8: warning: 'void stan::model::model_base_crtp<M>::write_array(stan::rng_t&, Eigen::VectorXd&, Eigen::VectorXd&, bool, bool, std::ostream*) const [with M = ulam_cmdstanr_790799fad754433849bd02c357aa0c90_model_namespace::ulam_cmdstanr_790799fad754433849bd02c357aa0c90_model; stan::rng_t = boost::random::mixmax_engine<17, 36, 0>; Eigen::VectorXd = Eigen::Matrix<double, -1, 1>; std::ostream = std::basic_ostream<char>]' was hidden [-Woverloaded-virtual=]
136 | void write_array(stan::rng_t& rng, Eigen::VectorXd& theta,
| ^~~~~~~~~~~
C:/Users/Zane/AppData/Local/Temp/RtmpSCWF6a/model-305c2285bf.hpp:508: note: by 'ulam_cmdstanr_790799fad754433849bd02c357aa0c90_model_namespace::ulam_cmdstanr_790799fad754433849bd02c357aa0c90_model::write_array'
508 | write_array(RNG& base_rng, std::vector<double>& params_r, std::vector<int>&
Running MCMC with 4 parallel chains, with 1 thread(s) per chain...
Chain 1 Iteration: 1 / 1000 [ 0%] (Warmup)
Chain 2 Iteration: 1 / 1000 [ 0%] (Warmup)
Chain 3 Iteration: 1 / 1000 [ 0%] (Warmup)
Chain 4 Iteration: 1 / 1000 [ 0%] (Warmup)
Chain 1 Iteration: 100 / 1000 [ 10%] (Warmup)
Chain 2 Iteration: 100 / 1000 [ 10%] (Warmup)
Chain 3 Iteration: 100 / 1000 [ 10%] (Warmup)
Chain 4 Iteration: 100 / 1000 [ 10%] (Warmup)
Chain 2 Iteration: 200 / 1000 [ 20%] (Warmup)
Chain 3 Iteration: 200 / 1000 [ 20%] (Warmup)
Chain 4 Iteration: 200 / 1000 [ 20%] (Warmup)
Chain 1 Iteration: 200 / 1000 [ 20%] (Warmup)
Chain 2 Iteration: 300 / 1000 [ 30%] (Warmup)
Chain 3 Iteration: 300 / 1000 [ 30%] (Warmup)
Chain 4 Iteration: 300 / 1000 [ 30%] (Warmup)
Chain 1 Iteration: 300 / 1000 [ 30%] (Warmup)
Chain 2 Iteration: 400 / 1000 [ 40%] (Warmup)
Chain 3 Iteration: 400 / 1000 [ 40%] (Warmup)
Chain 4 Iteration: 400 / 1000 [ 40%] (Warmup)
Chain 1 Iteration: 400 / 1000 [ 40%] (Warmup)
Chain 2 Iteration: 500 / 1000 [ 50%] (Warmup)
Chain 3 Iteration: 500 / 1000 [ 50%] (Warmup)
Chain 4 Iteration: 500 / 1000 [ 50%] (Warmup)
Chain 1 Iteration: 500 / 1000 [ 50%] (Warmup)
Chain 2 Iteration: 501 / 1000 [ 50%] (Sampling)
Chain 3 Iteration: 501 / 1000 [ 50%] (Sampling)
Chain 4 Iteration: 501 / 1000 [ 50%] (Sampling)
Chain 1 Iteration: 501 / 1000 [ 50%] (Sampling)
Chain 1 Iteration: 600 / 1000 [ 60%] (Sampling)
Chain 2 Iteration: 600 / 1000 [ 60%] (Sampling)
Chain 3 Iteration: 600 / 1000 [ 60%] (Sampling)
Chain 4 Iteration: 600 / 1000 [ 60%] (Sampling)
Chain 3 Iteration: 700 / 1000 [ 70%] (Sampling)
Chain 1 Iteration: 700 / 1000 [ 70%] (Sampling)
Chain 2 Iteration: 700 / 1000 [ 70%] (Sampling)
Chain 4 Iteration: 700 / 1000 [ 70%] (Sampling)
Chain 3 Iteration: 800 / 1000 [ 80%] (Sampling)
Chain 4 Iteration: 800 / 1000 [ 80%] (Sampling)
Chain 1 Iteration: 800 / 1000 [ 80%] (Sampling)
Chain 2 Iteration: 800 / 1000 [ 80%] (Sampling)
Chain 2 Iteration: 900 / 1000 [ 90%] (Sampling)
Chain 3 Iteration: 900 / 1000 [ 90%] (Sampling)
Chain 4 Iteration: 900 / 1000 [ 90%] (Sampling)
Chain 1 Iteration: 900 / 1000 [ 90%] (Sampling)
Chain 3 Iteration: 1000 / 1000 [100%] (Sampling)
Chain 4 Iteration: 1000 / 1000 [100%] (Sampling)
Chain 3 finished in 1.9 seconds.
Chain 4 finished in 1.9 seconds.
Chain 1 Iteration: 1000 / 1000 [100%] (Sampling)
Chain 2 Iteration: 1000 / 1000 [100%] (Sampling)
Chain 1 finished in 2.0 seconds.
Chain 2 finished in 2.0 seconds.
All 4 chains finished successfully.
Mean chain execution time: 1.9 seconds.
Total execution time: 2.1 seconds.
:: compare (.4 , m11.5 , m11.6 , m11.7 ,sort = "PSIS" , func = PSIS
PSIS SE dPSIS dSE pPSIS weight
m11.7 530.2222 19.05404 0.00000 NA 6.875426 0.750215500
m11.4 532.4716 18.97652 2.24947 2.637975 8.593902 0.243623869
m11.5 541.0905 17.90472 10.86829 7.175685 5.736835 0.003274658
m11.6 541.3432 18.36097 11.12100 7.594034 6.816366 0.002885973
While all four of the models are basically indistinguishable in terms of PSIS, the fact that m11.7 had the best PSIS and m11.7 and m11.4 were slightly better than m11.6 and m11.5, this could suggest that the prosoc_left variable is slightly more important than the condition variable.
11H2
For this problem, we’ll model salmon pirating attempts by bald eagles in Washington state. First we need to set up the data.
data (eagles, package = "MASS" )<- list (y = eagles$ y,n = eagles$ n,P = ifelse (eagles$ P == "S" , 0 , 1 ),A = ifelse (eagles$ A == "I" , 0 , 1 ),V = ifelse (eagles$ V == "S" , 0 , 1 )
First we’ll build a model that considers the three different predictors independently in an aggregated binomial framework. We want to fit this model with both quap and ulam and see if there are any major differences.
<- rethinking:: ulam (alist (~ dbinom (n, p),logit (p) <- a + bp * P + ba * A + bv * V,~ dnorm (0 , 1.5 ),~ dnorm (0 , 0.5 ),~ dnorm (0 , 0.5 ),~ dnorm (0 , 0.5 )data = eagle_data,chains = 4 , cores = 4
In file included from stan/src/stan/model/model_header.hpp:5:
stan/src/stan/model/model_base_crtp.hpp:205:8: warning: 'void stan::model::model_base_crtp<M>::write_array(stan::rng_t&, std::vector<double>&, std::vector<int>&, std::vector<double>&, bool, bool, std::ostream*) const [with M = ulam_cmdstanr_dc511ed7ea10c13f17266b49a99b8d99_model_namespace::ulam_cmdstanr_dc511ed7ea10c13f17266b49a99b8d99_model; stan::rng_t = boost::random::mixmax_engine<17, 36, 0>; std::ostream = std::basic_ostream<char>]' was hidden [-Woverloaded-virtual=]
205 | void write_array(stan::rng_t& rng, std::vector<double>& theta,
| ^~~~~~~~~~~
C:/Users/Zane/AppData/Local/Temp/RtmpSCWF6a/model-305c66dc7c79.hpp:445: note: by 'ulam_cmdstanr_dc511ed7ea10c13f17266b49a99b8d99_model_namespace::ulam_cmdstanr_dc511ed7ea10c13f17266b49a99b8d99_model::write_array'
445 | write_array(RNG& base_rng, std::vector<double>& params_r, std::vector<int>&
stan/src/stan/model/model_base_crtp.hpp:136:8: warning: 'void stan::model::model_base_crtp<M>::write_array(stan::rng_t&, Eigen::VectorXd&, Eigen::VectorXd&, bool, bool, std::ostream*) const [with M = ulam_cmdstanr_dc511ed7ea10c13f17266b49a99b8d99_model_namespace::ulam_cmdstanr_dc511ed7ea10c13f17266b49a99b8d99_model; stan::rng_t = boost::random::mixmax_engine<17, 36, 0>; Eigen::VectorXd = Eigen::Matrix<double, -1, 1>; std::ostream = std::basic_ostream<char>]' was hidden [-Woverloaded-virtual=]
136 | void write_array(stan::rng_t& rng, Eigen::VectorXd& theta,
| ^~~~~~~~~~~
C:/Users/Zane/AppData/Local/Temp/RtmpSCWF6a/model-305c66dc7c79.hpp:445: note: by 'ulam_cmdstanr_dc511ed7ea10c13f17266b49a99b8d99_model_namespace::ulam_cmdstanr_dc511ed7ea10c13f17266b49a99b8d99_model::write_array'
445 | write_array(RNG& base_rng, std::vector<double>& params_r, std::vector<int>&
Running MCMC with 4 parallel chains, with 1 thread(s) per chain...
Chain 1 Iteration: 1 / 1000 [ 0%] (Warmup)
Chain 1 Iteration: 100 / 1000 [ 10%] (Warmup)
Chain 1 Iteration: 200 / 1000 [ 20%] (Warmup)
Chain 1 Iteration: 300 / 1000 [ 30%] (Warmup)
Chain 1 Iteration: 400 / 1000 [ 40%] (Warmup)
Chain 1 Iteration: 500 / 1000 [ 50%] (Warmup)
Chain 1 Iteration: 501 / 1000 [ 50%] (Sampling)
Chain 1 Iteration: 600 / 1000 [ 60%] (Sampling)
Chain 1 Iteration: 700 / 1000 [ 70%] (Sampling)
Chain 1 Iteration: 800 / 1000 [ 80%] (Sampling)
Chain 1 Iteration: 900 / 1000 [ 90%] (Sampling)
Chain 1 Iteration: 1000 / 1000 [100%] (Sampling)
Chain 2 Iteration: 1 / 1000 [ 0%] (Warmup)
Chain 2 Iteration: 100 / 1000 [ 10%] (Warmup)
Chain 2 Iteration: 200 / 1000 [ 20%] (Warmup)
Chain 2 Iteration: 300 / 1000 [ 30%] (Warmup)
Chain 2 Iteration: 400 / 1000 [ 40%] (Warmup)
Chain 2 Iteration: 500 / 1000 [ 50%] (Warmup)
Chain 2 Iteration: 501 / 1000 [ 50%] (Sampling)
Chain 2 Iteration: 600 / 1000 [ 60%] (Sampling)
Chain 2 Iteration: 700 / 1000 [ 70%] (Sampling)
Chain 2 Iteration: 800 / 1000 [ 80%] (Sampling)
Chain 2 Iteration: 900 / 1000 [ 90%] (Sampling)
Chain 2 Iteration: 1000 / 1000 [100%] (Sampling)
Chain 3 Iteration: 1 / 1000 [ 0%] (Warmup)
Chain 3 Iteration: 100 / 1000 [ 10%] (Warmup)
Chain 3 Iteration: 200 / 1000 [ 20%] (Warmup)
Chain 3 Iteration: 300 / 1000 [ 30%] (Warmup)
Chain 3 Iteration: 400 / 1000 [ 40%] (Warmup)
Chain 3 Iteration: 500 / 1000 [ 50%] (Warmup)
Chain 3 Iteration: 501 / 1000 [ 50%] (Sampling)
Chain 3 Iteration: 600 / 1000 [ 60%] (Sampling)
Chain 3 Iteration: 700 / 1000 [ 70%] (Sampling)
Chain 3 Iteration: 800 / 1000 [ 80%] (Sampling)
Chain 3 Iteration: 900 / 1000 [ 90%] (Sampling)
Chain 3 Iteration: 1000 / 1000 [100%] (Sampling)
Chain 4 Iteration: 1 / 1000 [ 0%] (Warmup)
Chain 4 Iteration: 100 / 1000 [ 10%] (Warmup)
Chain 4 Iteration: 200 / 1000 [ 20%] (Warmup)
Chain 4 Iteration: 300 / 1000 [ 30%] (Warmup)
Chain 4 Iteration: 400 / 1000 [ 40%] (Warmup)
Chain 4 Iteration: 500 / 1000 [ 50%] (Warmup)
Chain 4 Iteration: 501 / 1000 [ 50%] (Sampling)
Chain 4 Iteration: 600 / 1000 [ 60%] (Sampling)
Chain 4 Iteration: 700 / 1000 [ 70%] (Sampling)
Chain 4 Iteration: 800 / 1000 [ 80%] (Sampling)
Chain 4 Iteration: 900 / 1000 [ 90%] (Sampling)
Chain 4 Iteration: 1000 / 1000 [100%] (Sampling)
Chain 1 finished in 0.1 seconds.
Chain 2 finished in 0.1 seconds.
Chain 3 finished in 0.1 seconds.
Chain 4 finished in 0.1 seconds.
All 4 chains finished successfully.
Mean chain execution time: 0.1 seconds.
Total execution time: 0.3 seconds.
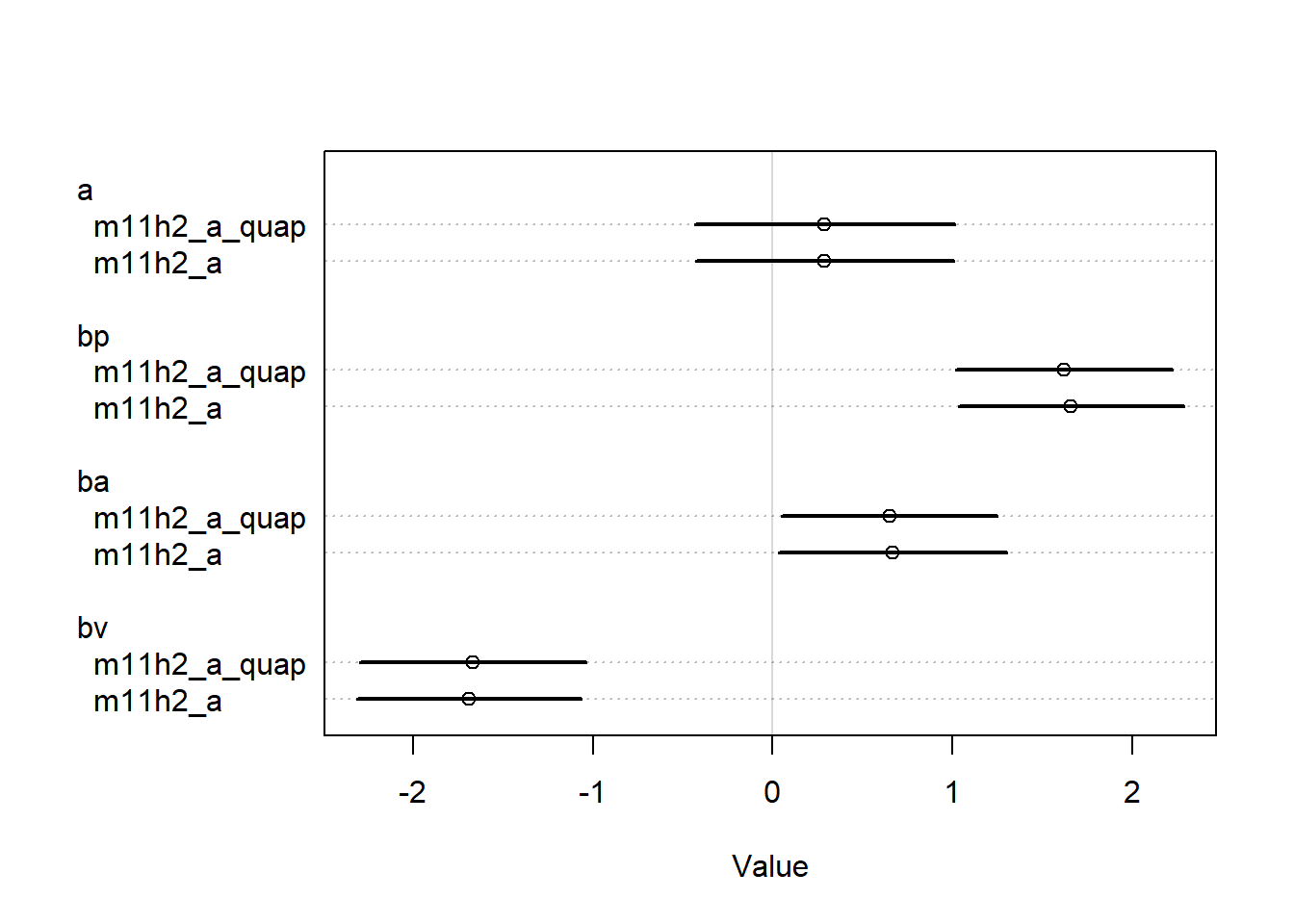
<- rethinking:: quap (alist (~ dbinom (n, p),logit (p) <- a + bp * P + ba * A + bv * V,~ dnorm (0 , 1.5 ),~ dnorm (0 , 0.5 ),~ dnorm (0 , 0.5 ),~ dnorm (0 , 0.5 )data = eagle_datalayout (1 ):: coeftab (m11h2_a, m11h2_a_quap) |> rethinking:: coeftab_plot ()
We can see that the quap estimates are identical, so we’ll use the quap estimates to get our predictions, I guess.
Now we need to intercept the estimates. We can first take a look at the coefficients.
:: precis (m11h2_a_quap)
mean sd 5.5% 94.5%
a 0.2936490 0.3681379 -0.2947064 0.8820044
bp 1.6211363 0.3063651 1.1315057 2.1107669
ba 0.6516624 0.3054238 0.1635362 1.1397886
bv -1.6731447 0.3191361 -2.1831858 -1.1631036
Wee see that the effects of \(P\) and \(A\) both seem to have their entire probability density at positive values, while the coefficient for \(V\) has a negative effect. However, these coefficients don’t tell us that much – we can exponentiate them to get some odds ratios, though.
:: precis (m11h2_a_quap, pars = c ("bp" , "ba" , "bv" )) |> unclass () |> as.data.frame () |> :: select (- sd) |> :: mutate (dplyr:: across (dplyr:: everything (), \(x) round (exp (x), 2 ))) |> ` rownames<- ` (c ("bp" , "ba" , "bv" ))
mean X5.5. X94.5.
bp 5.06 3.10 8.25
ba 1.92 1.18 3.13
bv 0.19 0.11 0.31
This gives us a bit more understandable estimate of the effect, but we really want to look at the predicted probabilities and success counts to really understand what is going on.
Code
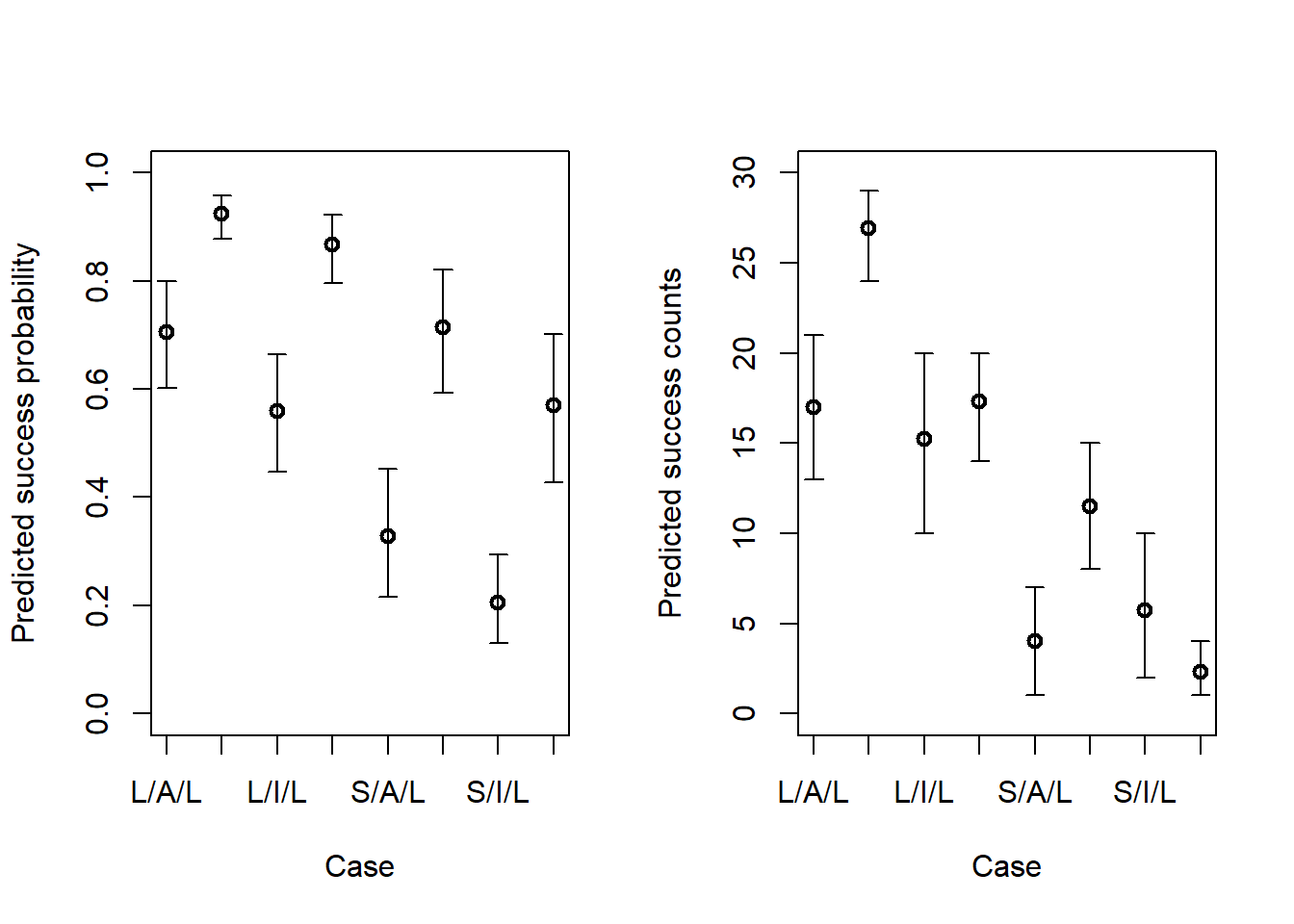
# Predicted probabilities <- rethinking:: link (m11h2_a_quap)<- apply (pred_probs, 2 , mean)<- apply (pred_probs, 2 , rethinking:: PI)# Predicted success counts <- rethinking:: sim (m11h2_a_quap)<- apply (pred_counts, 2 , mean)<- apply (pred_counts, 2 , rethinking:: PI)# Making plots <- paste (ifelse (eagle_data$ P == 0 , "S" , "L" ),ifelse (eagle_data$ A == 0 , "I" , "A" ),ifelse (eagle_data$ V == 0 , "S" , "L" ),sep = "/" layout (matrix (1 : 2 , nrow = 1 ))plot (1 : 8 , pred_prob_mean,xlab = "Case" ,ylab = "Predicted success probability" ,lwd = 2 ,xlim = c (1 , 8 ),ylim = c (0 , 1 ),xaxt = "n" axis (1 , at = 1 : 8 , labels = labs)arrows (x0 = 1 : 8 ,y0 = pred_prob_pi[1 , ],x = 1 : 8 ,y = pred_prob_pi[2 , ],length = 0.05 ,angle = 90 ,code = 3 plot (1 : 8 , pred_count_mean,xlab = "Case" ,ylab = "Predicted success counts" ,lwd = 2 ,xlim = c (1 , 8 ),ylim = c (0 , 30 ),xaxt = "n" axis (1 , at = 1 : 8 , labels = labs)arrows (x0 = 1 : 8 ,y0 = pred_count_pi[1 , ],x = 1 : 8 ,y = pred_count_pi[2 , ],length = 0.05 ,angle = 90 ,code = 3
In general, trying to understand three categorical effects simultaneously is a bit tough. But the cases on the x axis are three letters representing the size of the pirate, the age of the pirate, and the size of the victim respectively. We can see that, in general, pirating from a large bird is much less successful than pirating from a small bird, across all categories of pirate age and size. In general, it also looks like large, adult pirates are the most successful overall.
We can also plot this in a different way using a traditional interaction plot.
Code
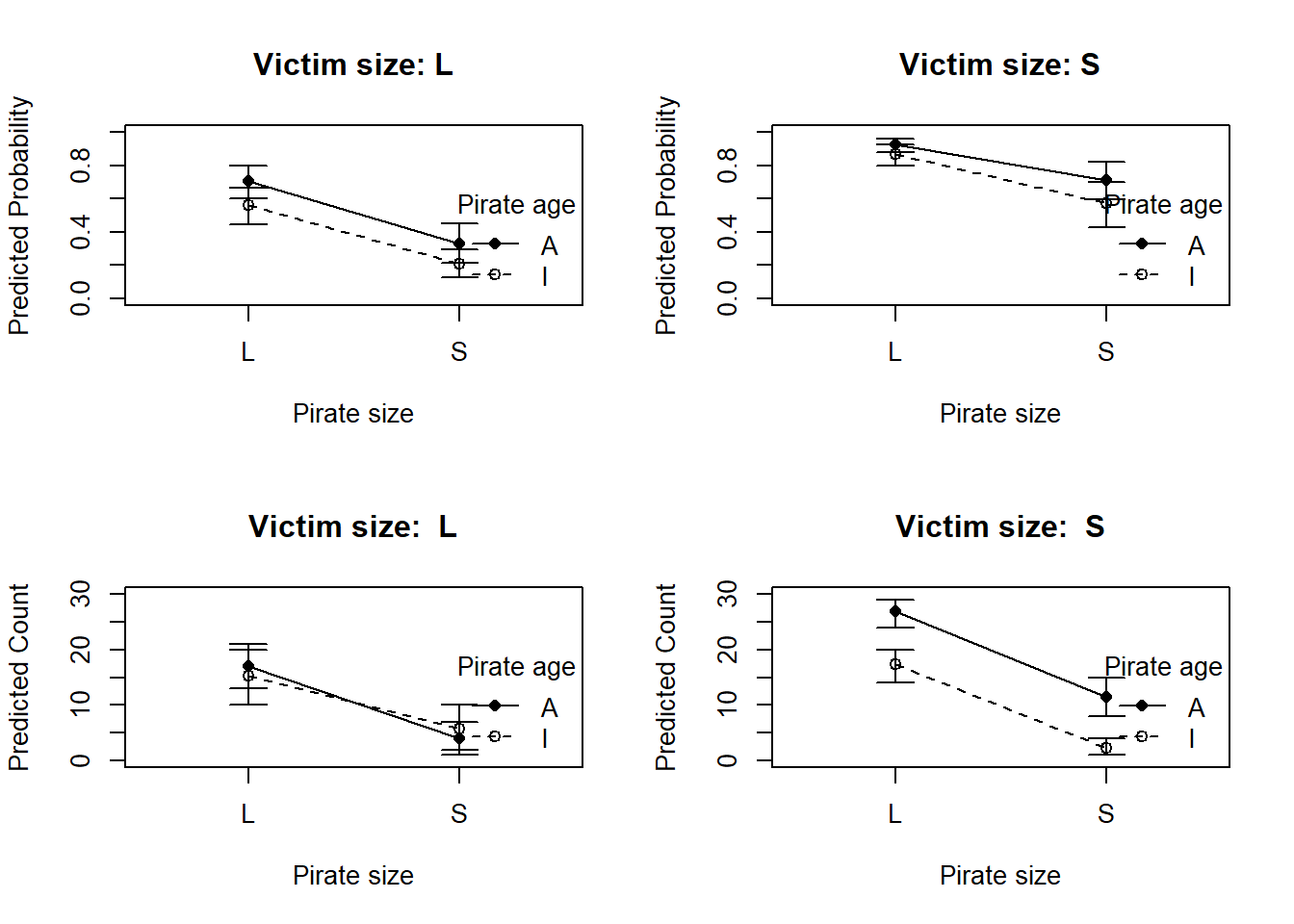
<- eagles |> :: mutate (pred_prob_mean = pred_prob_mean,pred_prob_lwr = pred_prob_pi[1 , ],pred_prob_upr = pred_prob_pi[2 , ],pred_count_mean = pred_count_mean,pred_count_lwr = pred_count_pi[1 , ],pred_count_upr = pred_count_pi[2 , ]layout (matrix (1 : 4 , nrow = 2 , byrow = TRUE ))# Set up plotting layout: one plot per level of V <- unique (edp$ V)# Define symbols and line types for A <- unique (edp$ A)<- c ("A" = 16 , "I" = 1 )<- c ("A" = 1 , "I" = 2 )for (v in V_levels) {<- edp[edp$ V == v, ]plot (NA , xlim = c (0.5 , 2.5 ), ylim = c (0 , 1 ), xaxt = "n" ,xlab = "Pirate size" , ylab = "Predicted Probability" , main = paste ("Victim size:" , v))axis (1 , at = 1 : 2 , labels = c ("L" , "S" ))for (a in A_levels) {<- sub[sub$ A == a, ]<- ifelse (dat$ P == "L" , 1 , 2 )# CI bars arrows (xvals, dat$ pred_prob_lwr, xvals, dat$ pred_prob_upr, angle = 90 , code = 3 , length = 0.1 , col = "black" )# Mean points and lines lines (xvals, dat$ pred_prob_mean, lty = lty_vals[a], col = "black" )points (xvals, dat$ pred_prob_mean, pch = pch_vals[a], col = "black" , bg = "black" )legend ("bottomright" , legend = A_levels,pch = pch_vals, lty = lty_vals, title = "Pirate age" , bty = "n" )# Set up plotting layout: one plot per level of V <- unique (edp$ V)# Define symbols and line types for A <- unique (edp$ A)<- c ("A" = 16 , "I" = 1 )<- c ("A" = 1 , "I" = 2 )for (v in V_levels) {<- edp[edp$ V == v, ]plot (NA , xlim = c (0.5 , 2.5 ), ylim = c (0 , 30 ), xaxt = "n" ,xlab = "Pirate size" , ylab = "Predicted Count" , main = paste ("Victim size: " , v))axis (1 , at = 1 : 2 , labels = c ("L" , "S" ))for (a in A_levels) {<- sub[sub$ A == a, ]<- ifelse (dat$ P == "L" , 1 , 2 )# CI bars arrows (xvals, dat$ pred_count_lwr, xvals, dat$ pred_count_upr, angle = 90 , code = 3 , length = 0.1 , col = "black" )# Mean points and lines lines (xvals, dat$ pred_count_mean, lty = lty_vals[a], col = "black" )points (xvals, dat$ pred_count_mean, pch = pch_vals[a], col = "black" , bg = "black" )legend ("bottomright" , legend = A_levels,pch = pch_vals, lty = lty_vals, title = "Pirate age" , bty = "n" )
Since we already saw that the affect of victim size was important, I made that variable the faceting variable here to see if we can visually see any interactions between pirate age and size, since we’ll look at that in the next problem. The CI’s overlap a lot, but in general it seems adult pirates are generally better, but pirate size appears to be more important in determining overall success.
In a real analysis, we should also look at the marginal effects of each predictor (how much we expect success probability or count to increase if we change one variable at a time, which is NOT estimated by the odds ratio due to the nonlinear link function), but we haven’t really discussed that at this point in the book so I’ll ignore it.
Next we’ll fit a model with an iteraction between pirate size and age, and compare the models with WAIC. Just for fun, I also decided to compare the models with all two-way interactions, and a model that also has a three-way interaction. But first we’ll answer the actual question.
<- rethinking:: quap (alist (~ dbinom (n, p),logit (p) <- a + bp * P + ba * A + bv * V + gpa * P * A,~ dnorm (0 , 1.5 ),~ dnorm (0 , 0.5 ),~ dnorm (0 , 0.5 ),~ dnorm (0 , 0.5 ),~ dnorm (0 , 0.25 )data = eagle_data<- rethinking:: quap (alist (~ dbinom (n, p),logit (p) <- a + bp * P + ba * A + bv * V + * P * A + gpv * P * V + gav * A * V,~ dnorm (0 , 1.5 ),~ dnorm (0 , 0.5 ),~ dnorm (0 , 0.5 ),~ dnorm (0 , 0.5 ),~ dnorm (0 , 0.25 ),~ dnorm (0 , 0.25 ),~ dnorm (0 , 0.25 )data = eagle_data<- rethinking:: quap (alist (~ dbinom (n, p),logit (p) <- a + bp * P + ba * A + bv * V + * P * A + gpv * P * V + gav * A * V + * P * A * V,~ dnorm (0 , 1.5 ),~ dnorm (0 , 0.5 ),~ dnorm (0 , 0.5 ),~ dnorm (0 , 0.5 ),~ dnorm (0 , 0.25 ),~ dnorm (0 , 0.25 ),~ dnorm (0 , 0.25 ),~ dnorm (0 , 0.125 )data = eagle_data
So like I said, first we’ll answer the actual question.
:: compare (m11h2_a_quap, m11h2_c)
WAIC SE dWAIC dSE pWAIC weight
m11h2_a_quap 59.21206 11.29599 0.0000000 NA 8.235358 0.5142964
m11h2_c 59.32646 11.41087 0.1144025 0.8295544 8.269835 0.4857036
The two models are basically equivalent in WAIC, indicating that pirate age and pirate size do not seem to interact. Probably large birds are always more likely to succeed and small birds are always more likely to fail, regardless of whether they are adults, and any learned experience in how to pirate is independent of the bird’s size.
If we compare all of the models with interaction terms, we can see that in general none of the interaction terms make the model do better than the original model with no interactions. I wonder if this is mostly because we have small counts of some combinations – in general, we were much less likely to observe small birds acting as pirates in the first place, and we were less likely to observe successes across all of the small pirate groups.
:: compare (m11h2_a_quap, m11h2_c, m11h2_d, m11h2_e)
WAIC SE dWAIC dSE pWAIC weight
m11h2_a_quap 58.82845 11.48208 0.0000000 NA 7.870400 0.3574550
m11h2_e 59.50629 11.44157 0.6778414 1.1042359 8.791410 0.2547006
m11h2_c 59.80259 11.86056 0.9741382 0.8174611 8.423275 0.2196291
m11h2_d 60.33598 12.38814 1.5075296 1.4153978 9.062191 0.1682153
11H3
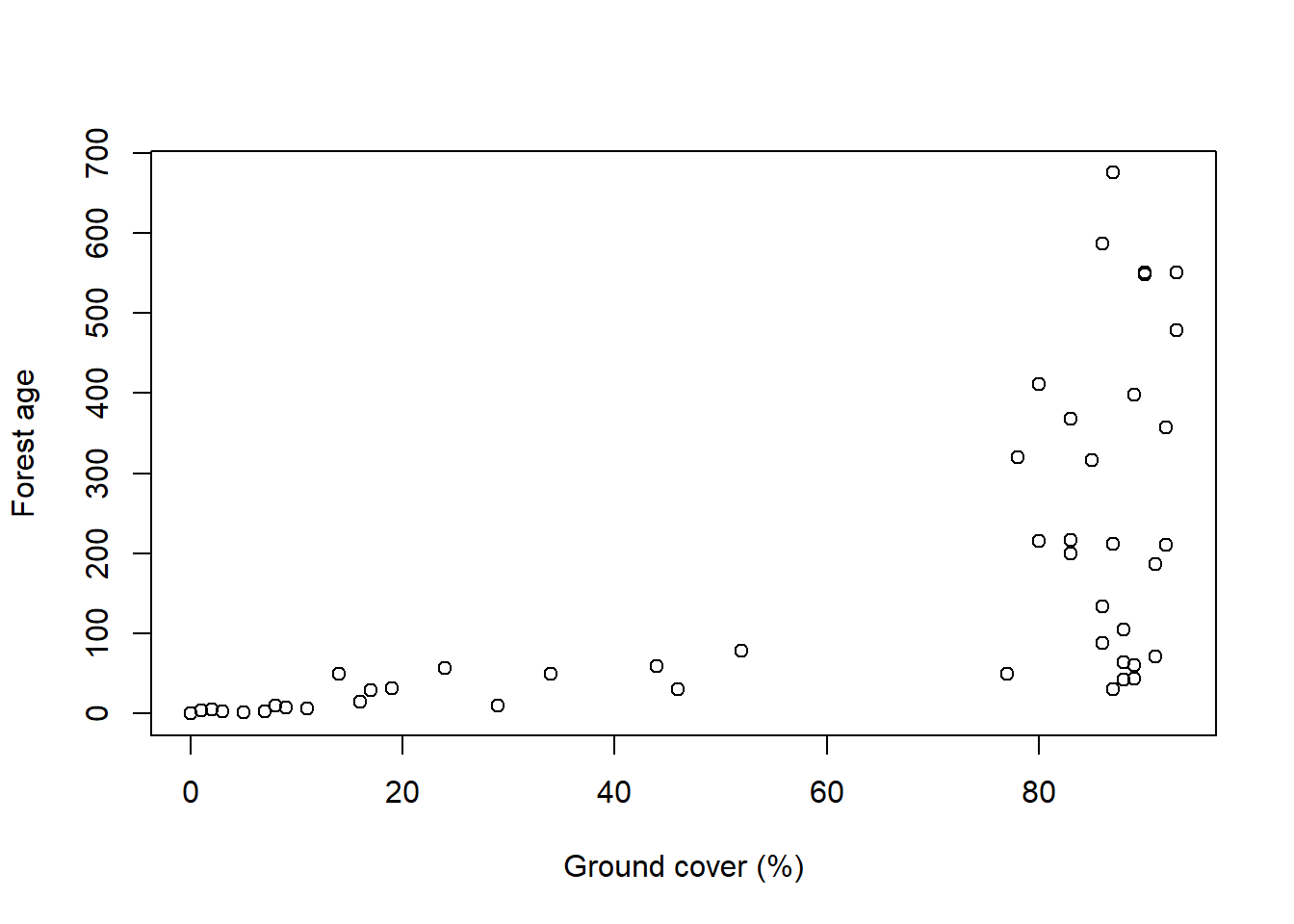
For this problem, we’ll build a model of salamander density, so we better start by cleaning up the salamander data. I kept getting really shitty models until I realized I needed to standardize the predictors because the scale is so different from the count scale of the outcome. But once I did that, I got models that worked alright.
data ("salamanders" , package = "rethinking" )<- list (n = salamanders$ SALAMAN,gc = standardize (salamanders$ PCTCOVER),fa = standardize (salamanders$ FORESTAGE)
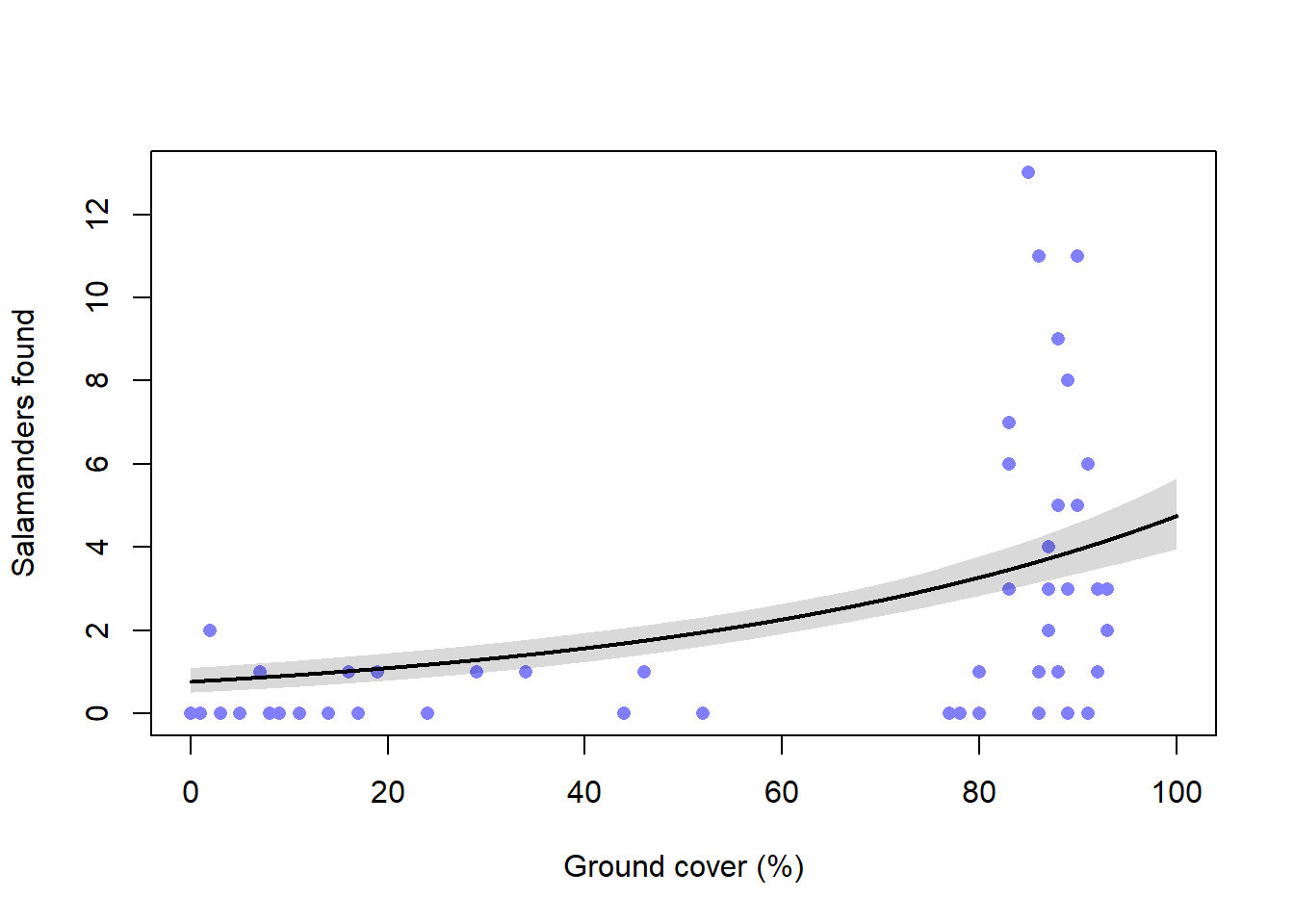
First we’ll build a model relating salamander density to percent cover using a Poisson model. Again we need to compare quap and ulam.
<- rethinking:: ulam (alist (~ dpois (lambda),log (lambda) <- a + bg * gc,~ dnorm (3 , 0.5 ),~ dnorm (0 , 0.2 )data = s_dat,chains = 4 , cores = 4 ,log_lik = TRUE
In file included from stan/src/stan/model/model_header.hpp:5:
stan/src/stan/model/model_base_crtp.hpp:205:8: warning: 'void stan::model::model_base_crtp<M>::write_array(stan::rng_t&, std::vector<double>&, std::vector<int>&, std::vector<double>&, bool, bool, std::ostream*) const [with M = ulam_cmdstanr_55fa12cdc55a5ce3c1c627d810695ba0_model_namespace::ulam_cmdstanr_55fa12cdc55a5ce3c1c627d810695ba0_model; stan::rng_t = boost::random::mixmax_engine<17, 36, 0>; std::ostream = std::basic_ostream<char>]' was hidden [-Woverloaded-virtual=]
205 | void write_array(stan::rng_t& rng, std::vector<double>& theta,
| ^~~~~~~~~~~
C:/Users/Zane/AppData/Local/Temp/RtmpSCWF6a/model-305c2f397abf.hpp:460: note: by 'ulam_cmdstanr_55fa12cdc55a5ce3c1c627d810695ba0_model_namespace::ulam_cmdstanr_55fa12cdc55a5ce3c1c627d810695ba0_model::write_array'
460 | write_array(RNG& base_rng, std::vector<double>& params_r, std::vector<int>&
stan/src/stan/model/model_base_crtp.hpp:136:8: warning: 'void stan::model::model_base_crtp<M>::write_array(stan::rng_t&, Eigen::VectorXd&, Eigen::VectorXd&, bool, bool, std::ostream*) const [with M = ulam_cmdstanr_55fa12cdc55a5ce3c1c627d810695ba0_model_namespace::ulam_cmdstanr_55fa12cdc55a5ce3c1c627d810695ba0_model; stan::rng_t = boost::random::mixmax_engine<17, 36, 0>; Eigen::VectorXd = Eigen::Matrix<double, -1, 1>; std::ostream = std::basic_ostream<char>]' was hidden [-Woverloaded-virtual=]
136 | void write_array(stan::rng_t& rng, Eigen::VectorXd& theta,
| ^~~~~~~~~~~
C:/Users/Zane/AppData/Local/Temp/RtmpSCWF6a/model-305c2f397abf.hpp:460: note: by 'ulam_cmdstanr_55fa12cdc55a5ce3c1c627d810695ba0_model_namespace::ulam_cmdstanr_55fa12cdc55a5ce3c1c627d810695ba0_model::write_array'
460 | write_array(RNG& base_rng, std::vector<double>& params_r, std::vector<int>&
Running MCMC with 4 parallel chains, with 1 thread(s) per chain...
Chain 1 Iteration: 1 / 1000 [ 0%] (Warmup)
Chain 1 Iteration: 100 / 1000 [ 10%] (Warmup)
Chain 1 Iteration: 200 / 1000 [ 20%] (Warmup)
Chain 1 Iteration: 300 / 1000 [ 30%] (Warmup)
Chain 1 Iteration: 400 / 1000 [ 40%] (Warmup)
Chain 1 Iteration: 500 / 1000 [ 50%] (Warmup)
Chain 1 Iteration: 501 / 1000 [ 50%] (Sampling)
Chain 1 Iteration: 600 / 1000 [ 60%] (Sampling)
Chain 1 Iteration: 700 / 1000 [ 70%] (Sampling)
Chain 1 Iteration: 800 / 1000 [ 80%] (Sampling)
Chain 2 Iteration: 1 / 1000 [ 0%] (Warmup)
Chain 2 Iteration: 100 / 1000 [ 10%] (Warmup)
Chain 2 Iteration: 200 / 1000 [ 20%] (Warmup)
Chain 2 Iteration: 300 / 1000 [ 30%] (Warmup)
Chain 2 Iteration: 400 / 1000 [ 40%] (Warmup)
Chain 2 Iteration: 500 / 1000 [ 50%] (Warmup)
Chain 2 Iteration: 501 / 1000 [ 50%] (Sampling)
Chain 2 Iteration: 600 / 1000 [ 60%] (Sampling)
Chain 2 Iteration: 700 / 1000 [ 70%] (Sampling)
Chain 2 Iteration: 800 / 1000 [ 80%] (Sampling)
Chain 2 Iteration: 900 / 1000 [ 90%] (Sampling)
Chain 3 Iteration: 1 / 1000 [ 0%] (Warmup)
Chain 3 Iteration: 100 / 1000 [ 10%] (Warmup)
Chain 3 Iteration: 200 / 1000 [ 20%] (Warmup)
Chain 3 Iteration: 300 / 1000 [ 30%] (Warmup)
Chain 3 Iteration: 400 / 1000 [ 40%] (Warmup)
Chain 3 Iteration: 500 / 1000 [ 50%] (Warmup)
Chain 3 Iteration: 501 / 1000 [ 50%] (Sampling)
Chain 3 Iteration: 600 / 1000 [ 60%] (Sampling)
Chain 3 Iteration: 700 / 1000 [ 70%] (Sampling)
Chain 3 Iteration: 800 / 1000 [ 80%] (Sampling)
Chain 3 Iteration: 900 / 1000 [ 90%] (Sampling)
Chain 4 Iteration: 1 / 1000 [ 0%] (Warmup)
Chain 4 Iteration: 100 / 1000 [ 10%] (Warmup)
Chain 4 Iteration: 200 / 1000 [ 20%] (Warmup)
Chain 4 Iteration: 300 / 1000 [ 30%] (Warmup)
Chain 4 Iteration: 400 / 1000 [ 40%] (Warmup)
Chain 4 Iteration: 500 / 1000 [ 50%] (Warmup)
Chain 4 Iteration: 501 / 1000 [ 50%] (Sampling)
Chain 4 Iteration: 600 / 1000 [ 60%] (Sampling)
Chain 1 Iteration: 900 / 1000 [ 90%] (Sampling)
Chain 1 Iteration: 1000 / 1000 [100%] (Sampling)
Chain 1 finished in 0.1 seconds.
Chain 2 Iteration: 1000 / 1000 [100%] (Sampling)
Chain 2 finished in 0.1 seconds.
Chain 3 Iteration: 1000 / 1000 [100%] (Sampling)
Chain 3 finished in 0.1 seconds.
Chain 4 Iteration: 700 / 1000 [ 70%] (Sampling)
Chain 4 Iteration: 800 / 1000 [ 80%] (Sampling)
Chain 4 Iteration: 900 / 1000 [ 90%] (Sampling)
Chain 4 Iteration: 1000 / 1000 [100%] (Sampling)
Chain 4 finished in 0.1 seconds.
All 4 chains finished successfully.
Mean chain execution time: 0.1 seconds.
Total execution time: 0.3 seconds.
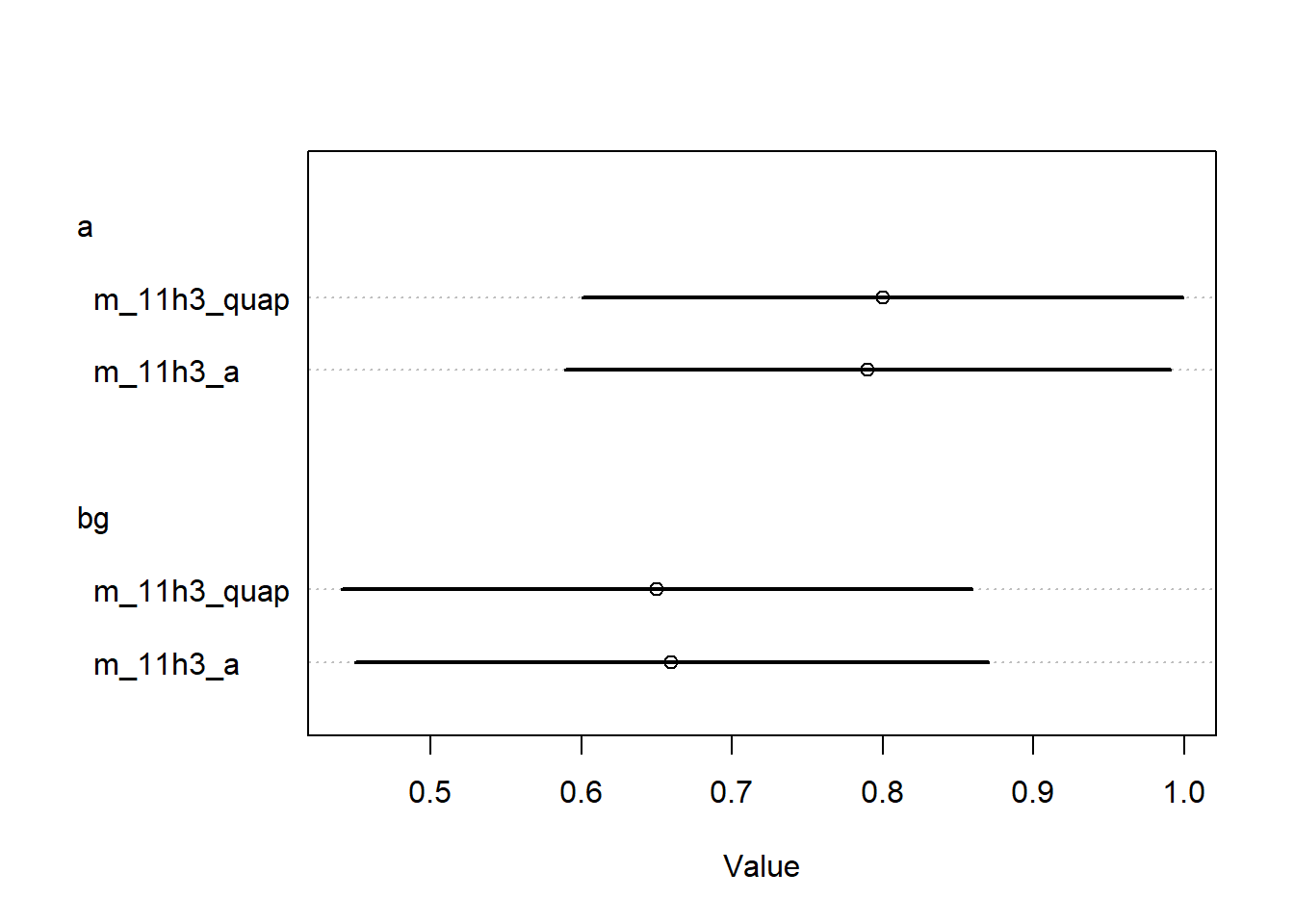
<- rethinking:: quap (alist (~ dpois (lambda),log (lambda) <- a + bg * gc,~ dnorm (3 , 0.5 ),~ dnorm (0 , 0.2 )data = s_datlayout (1 ):: coeftab (m_11h3_a, m_11h3_quap) |> rethinking:: coeftab_plot ()
Yet again, the two models are exactly the same. Based on my other readings, quadratic/laplace approximation tends to work really well for GLMs, especially simple GLMs. So hopefully we can either stop comparing these or do an example where there’s actually a difference. Anyways, let’s take a quick look at the coefficients from the HMC model.
:: precis (m_11h3_a)
mean sd 5.5% 94.5% rhat ess_bulk
a 0.7918713 0.1021981 0.6244364 0.9512355 1.000372 952.5662
bg 0.6632452 0.1069738 0.4883054 0.8321455 1.001730 1030.6920
We can see that the rate ratio is \(1.92 \ (1.60, 2.29)\) , which means that for every one standard deviation increase in ground cover of a site, we expect the count of salamanders to be multiplied by \(1.92\) . Let’s go ahead and plot the count predictions though, so we can understand what’s going on.
<- seq (0 , 100 , 0.01 )<- (gc_seq - attr (s_dat$ gc, "scaled:center" )) / attr (s_dat$ gc, "scaled:scale" )<- rethinking:: link (m_11h3_a, data = data.frame (gc = gc_seq_scaled))<- apply (preds, 2 , mean)<- apply (preds, 2 , rethinking:: PI)plot ($ PCTCOVER, s_dat$ n,lwd = 2 ,col = rethinking:: rangi2,xlab = "Ground cover (%)" ,ylab = "Salamanders found" ,xlim = c (0 , 100 ),pch = 16 :: shade (pred_pi, gc_seq)lines (lwd = 2
In this plot, the blue lines show the actual data, the solid line and ribbon show the estimated mean with its \(89\%\) credible interval.
We can see that the model makes generally decent predictions for the low value of ground cover, but the linear model we assumed doesn’t really make sense at the higher values of ground cover, where there is a big range of captured salamanders for very similar values of ground cover. Honestly, there aren’t really any models that only depend on ground cover that will do a good job explaining that – either those high ground covers just have high variability of salamander counts, or there’s another factor that can help us distinguish why sites with the same ground cover percentage are so variable.
Speaking of that, we want to add the forest age to our model. We’ll fit a model that has both predictors independently and a model that has a linear interaction.
<- rethinking:: ulam (alist (~ dpois (lambda),log (lambda) <- a + bg * gc + bf * fa,~ dnorm (3 , 0.5 ),~ dnorm (0 , 0.2 ),~ dnorm (0 , 0.2 )data = s_dat,chains = 4 , cores = 4 ,log_lik = TRUE
In file included from stan/src/stan/model/model_header.hpp:5:
stan/src/stan/model/model_base_crtp.hpp:205:8: warning: 'void stan::model::model_base_crtp<M>::write_array(stan::rng_t&, std::vector<double>&, std::vector<int>&, std::vector<double>&, bool, bool, std::ostream*) const [with M = ulam_cmdstanr_7062a07868a01f189545eca63ead032f_model_namespace::ulam_cmdstanr_7062a07868a01f189545eca63ead032f_model; stan::rng_t = boost::random::mixmax_engine<17, 36, 0>; std::ostream = std::basic_ostream<char>]' was hidden [-Woverloaded-virtual=]
205 | void write_array(stan::rng_t& rng, std::vector<double>& theta,
| ^~~~~~~~~~~
C:/Users/Zane/AppData/Local/Temp/RtmpSCWF6a/model-305c454f341.hpp:492: note: by 'ulam_cmdstanr_7062a07868a01f189545eca63ead032f_model_namespace::ulam_cmdstanr_7062a07868a01f189545eca63ead032f_model::write_array'
492 | write_array(RNG& base_rng, std::vector<double>& params_r, std::vector<int>&
stan/src/stan/model/model_base_crtp.hpp:136:8: warning: 'void stan::model::model_base_crtp<M>::write_array(stan::rng_t&, Eigen::VectorXd&, Eigen::VectorXd&, bool, bool, std::ostream*) const [with M = ulam_cmdstanr_7062a07868a01f189545eca63ead032f_model_namespace::ulam_cmdstanr_7062a07868a01f189545eca63ead032f_model; stan::rng_t = boost::random::mixmax_engine<17, 36, 0>; Eigen::VectorXd = Eigen::Matrix<double, -1, 1>; std::ostream = std::basic_ostream<char>]' was hidden [-Woverloaded-virtual=]
136 | void write_array(stan::rng_t& rng, Eigen::VectorXd& theta,
| ^~~~~~~~~~~
C:/Users/Zane/AppData/Local/Temp/RtmpSCWF6a/model-305c454f341.hpp:492: note: by 'ulam_cmdstanr_7062a07868a01f189545eca63ead032f_model_namespace::ulam_cmdstanr_7062a07868a01f189545eca63ead032f_model::write_array'
492 | write_array(RNG& base_rng, std::vector<double>& params_r, std::vector<int>&
Running MCMC with 4 parallel chains, with 1 thread(s) per chain...
Chain 1 Iteration: 1 / 1000 [ 0%] (Warmup)
Chain 1 Iteration: 100 / 1000 [ 10%] (Warmup)
Chain 1 Iteration: 200 / 1000 [ 20%] (Warmup)
Chain 1 Iteration: 300 / 1000 [ 30%] (Warmup)
Chain 1 Iteration: 400 / 1000 [ 40%] (Warmup)
Chain 1 Iteration: 500 / 1000 [ 50%] (Warmup)
Chain 1 Iteration: 501 / 1000 [ 50%] (Sampling)
Chain 1 Iteration: 600 / 1000 [ 60%] (Sampling)
Chain 1 Iteration: 700 / 1000 [ 70%] (Sampling)
Chain 1 Iteration: 800 / 1000 [ 80%] (Sampling)
Chain 1 Iteration: 900 / 1000 [ 90%] (Sampling)
Chain 2 Iteration: 1 / 1000 [ 0%] (Warmup)
Chain 2 Iteration: 100 / 1000 [ 10%] (Warmup)
Chain 2 Iteration: 200 / 1000 [ 20%] (Warmup)
Chain 2 Iteration: 300 / 1000 [ 30%] (Warmup)
Chain 2 Iteration: 400 / 1000 [ 40%] (Warmup)
Chain 2 Iteration: 500 / 1000 [ 50%] (Warmup)
Chain 2 Iteration: 501 / 1000 [ 50%] (Sampling)
Chain 2 Iteration: 600 / 1000 [ 60%] (Sampling)
Chain 2 Iteration: 700 / 1000 [ 70%] (Sampling)
Chain 3 Iteration: 1 / 1000 [ 0%] (Warmup)
Chain 3 Iteration: 100 / 1000 [ 10%] (Warmup)
Chain 3 Iteration: 200 / 1000 [ 20%] (Warmup)
Chain 3 Iteration: 300 / 1000 [ 30%] (Warmup)
Chain 3 Iteration: 400 / 1000 [ 40%] (Warmup)
Chain 3 Iteration: 500 / 1000 [ 50%] (Warmup)
Chain 3 Iteration: 501 / 1000 [ 50%] (Sampling)
Chain 3 Iteration: 600 / 1000 [ 60%] (Sampling)
Chain 4 Iteration: 1 / 1000 [ 0%] (Warmup)
Chain 4 Iteration: 100 / 1000 [ 10%] (Warmup)
Chain 4 Iteration: 200 / 1000 [ 20%] (Warmup)
Chain 4 Iteration: 300 / 1000 [ 30%] (Warmup)
Chain 4 Iteration: 400 / 1000 [ 40%] (Warmup)
Chain 4 Iteration: 500 / 1000 [ 50%] (Warmup)
Chain 4 Iteration: 501 / 1000 [ 50%] (Sampling)
Chain 4 Iteration: 600 / 1000 [ 60%] (Sampling)
Chain 4 Iteration: 700 / 1000 [ 70%] (Sampling)
Chain 1 Iteration: 1000 / 1000 [100%] (Sampling)
Chain 1 finished in 0.1 seconds.
Chain 2 Iteration: 800 / 1000 [ 80%] (Sampling)
Chain 2 Iteration: 900 / 1000 [ 90%] (Sampling)
Chain 2 Iteration: 1000 / 1000 [100%] (Sampling)
Chain 2 finished in 0.1 seconds.
Chain 3 Iteration: 700 / 1000 [ 70%] (Sampling)
Chain 3 Iteration: 800 / 1000 [ 80%] (Sampling)
Chain 3 Iteration: 900 / 1000 [ 90%] (Sampling)
Chain 3 Iteration: 1000 / 1000 [100%] (Sampling)
Chain 3 finished in 0.1 seconds.
Chain 4 Iteration: 800 / 1000 [ 80%] (Sampling)
Chain 4 Iteration: 900 / 1000 [ 90%] (Sampling)
Chain 4 Iteration: 1000 / 1000 [100%] (Sampling)
Chain 4 finished in 0.1 seconds.
All 4 chains finished successfully.
Mean chain execution time: 0.1 seconds.
Total execution time: 0.3 seconds.
<- rethinking:: ulam (alist (~ dpois (lambda),log (lambda) <- a + bg * gc + bf * fa + g * gc * fa,~ dnorm (3 , 0.5 ),~ dnorm (0 , 0.2 ),~ dnorm (0 , 0.2 ),~ dnorm (0 , 0.05 )data = s_dat,chains = 4 , cores = 4 ,log_lik = TRUE
In file included from stan/src/stan/model/model_header.hpp:5:
stan/src/stan/model/model_base_crtp.hpp:205:8: warning: 'void stan::model::model_base_crtp<M>::write_array(stan::rng_t&, std::vector<double>&, std::vector<int>&, std::vector<double>&, bool, bool, std::ostream*) const [with M = ulam_cmdstanr_0b5d6755af659527a2ddc7fb837d3966_model_namespace::ulam_cmdstanr_0b5d6755af659527a2ddc7fb837d3966_model; stan::rng_t = boost::random::mixmax_engine<17, 36, 0>; std::ostream = std::basic_ostream<char>]' was hidden [-Woverloaded-virtual=]
205 | void write_array(stan::rng_t& rng, std::vector<double>& theta,
| ^~~~~~~~~~~
C:/Users/Zane/AppData/Local/Temp/RtmpSCWF6a/model-305c1d661464.hpp:528: note: by 'ulam_cmdstanr_0b5d6755af659527a2ddc7fb837d3966_model_namespace::ulam_cmdstanr_0b5d6755af659527a2ddc7fb837d3966_model::write_array'
528 | write_array(RNG& base_rng, std::vector<double>& params_r, std::vector<int>&
stan/src/stan/model/model_base_crtp.hpp:136:8: warning: 'void stan::model::model_base_crtp<M>::write_array(stan::rng_t&, Eigen::VectorXd&, Eigen::VectorXd&, bool, bool, std::ostream*) const [with M = ulam_cmdstanr_0b5d6755af659527a2ddc7fb837d3966_model_namespace::ulam_cmdstanr_0b5d6755af659527a2ddc7fb837d3966_model; stan::rng_t = boost::random::mixmax_engine<17, 36, 0>; Eigen::VectorXd = Eigen::Matrix<double, -1, 1>; std::ostream = std::basic_ostream<char>]' was hidden [-Woverloaded-virtual=]
136 | void write_array(stan::rng_t& rng, Eigen::VectorXd& theta,
| ^~~~~~~~~~~
C:/Users/Zane/AppData/Local/Temp/RtmpSCWF6a/model-305c1d661464.hpp:528: note: by 'ulam_cmdstanr_0b5d6755af659527a2ddc7fb837d3966_model_namespace::ulam_cmdstanr_0b5d6755af659527a2ddc7fb837d3966_model::write_array'
528 | write_array(RNG& base_rng, std::vector<double>& params_r, std::vector<int>&
Running MCMC with 4 parallel chains, with 1 thread(s) per chain...
Chain 1 Iteration: 1 / 1000 [ 0%] (Warmup)
Chain 1 Iteration: 100 / 1000 [ 10%] (Warmup)
Chain 1 Iteration: 200 / 1000 [ 20%] (Warmup)
Chain 1 Iteration: 300 / 1000 [ 30%] (Warmup)
Chain 1 Iteration: 400 / 1000 [ 40%] (Warmup)
Chain 1 Iteration: 500 / 1000 [ 50%] (Warmup)
Chain 1 Iteration: 501 / 1000 [ 50%] (Sampling)
Chain 1 Iteration: 600 / 1000 [ 60%] (Sampling)
Chain 1 Iteration: 700 / 1000 [ 70%] (Sampling)
Chain 1 Iteration: 800 / 1000 [ 80%] (Sampling)
Chain 2 Iteration: 1 / 1000 [ 0%] (Warmup)
Chain 2 Iteration: 100 / 1000 [ 10%] (Warmup)
Chain 2 Iteration: 200 / 1000 [ 20%] (Warmup)
Chain 2 Iteration: 300 / 1000 [ 30%] (Warmup)
Chain 2 Iteration: 400 / 1000 [ 40%] (Warmup)
Chain 2 Iteration: 500 / 1000 [ 50%] (Warmup)
Chain 2 Iteration: 501 / 1000 [ 50%] (Sampling)
Chain 2 Iteration: 600 / 1000 [ 60%] (Sampling)
Chain 2 Iteration: 700 / 1000 [ 70%] (Sampling)
Chain 2 Iteration: 800 / 1000 [ 80%] (Sampling)
Chain 3 Iteration: 1 / 1000 [ 0%] (Warmup)
Chain 3 Iteration: 100 / 1000 [ 10%] (Warmup)
Chain 3 Iteration: 200 / 1000 [ 20%] (Warmup)
Chain 3 Iteration: 300 / 1000 [ 30%] (Warmup)
Chain 3 Iteration: 400 / 1000 [ 40%] (Warmup)
Chain 3 Iteration: 500 / 1000 [ 50%] (Warmup)
Chain 3 Iteration: 501 / 1000 [ 50%] (Sampling)
Chain 3 Iteration: 600 / 1000 [ 60%] (Sampling)
Chain 3 Iteration: 700 / 1000 [ 70%] (Sampling)
Chain 4 Iteration: 1 / 1000 [ 0%] (Warmup)
Chain 4 Iteration: 100 / 1000 [ 10%] (Warmup)
Chain 4 Iteration: 200 / 1000 [ 20%] (Warmup)
Chain 4 Iteration: 300 / 1000 [ 30%] (Warmup)
Chain 4 Iteration: 400 / 1000 [ 40%] (Warmup)
Chain 4 Iteration: 500 / 1000 [ 50%] (Warmup)
Chain 4 Iteration: 501 / 1000 [ 50%] (Sampling)
Chain 4 Iteration: 600 / 1000 [ 60%] (Sampling)
Chain 4 Iteration: 700 / 1000 [ 70%] (Sampling)
Chain 1 Iteration: 900 / 1000 [ 90%] (Sampling)
Chain 1 Iteration: 1000 / 1000 [100%] (Sampling)
Chain 1 finished in 0.1 seconds.
Chain 2 Iteration: 900 / 1000 [ 90%] (Sampling)
Chain 2 Iteration: 1000 / 1000 [100%] (Sampling)
Chain 2 finished in 0.1 seconds.
Chain 3 Iteration: 800 / 1000 [ 80%] (Sampling)
Chain 3 Iteration: 900 / 1000 [ 90%] (Sampling)
Chain 3 Iteration: 1000 / 1000 [100%] (Sampling)
Chain 3 finished in 0.1 seconds.
Chain 4 Iteration: 800 / 1000 [ 80%] (Sampling)
Chain 4 Iteration: 900 / 1000 [ 90%] (Sampling)
Chain 4 Iteration: 1000 / 1000 [100%] (Sampling)
Chain 4 finished in 0.1 seconds.
All 4 chains finished successfully.
Mean chain execution time: 0.1 seconds.
Total execution time: 0.3 seconds.
:: coeftab (m_11h3_a, m_11h3_b, m_11h3_c) |> :: coeftab_plot ()
The estimates for the intercept and the coefficient for ground cover move around a bit, but the estimates for the effect of forest age and the interaction term don’t seem to do all that much, or at least the effect is quite variable. Let’s look at the PSIS estimates to see if either of these models help our predictive power.
:: compare (sort = "PSIS" , func = PSIS
Some Pareto k values are high (>0.5). Set pointwise=TRUE to inspect individual points.
PSIS SE dPSIS dSE pPSIS weight
m_11h3_a 221.3605 25.04306 0.000000 NA 3.885854 0.78401151
m_11h3_c 224.9586 25.70290 3.598029 2.807431 6.488786 0.12972398
m_11h3_b 225.7745 25.99503 4.414011 3.106585 6.829138 0.08626451
Some of the \(k\) values are high, so we have a few influential points. But I don’t think we need to look at those, because we can see the three models are essentially identical, with the model with only ground cover coming in slightly on top, though the SEs are extremely large copared to the dPSIS. Now let’s try to figure out why the forest age isn’t helping our model. If we look at the relationship between the two covariates, we see that it does seemingly have the potential to help with the problem I mentioned before.
plot ($ PCTCOVER,$ FORESTAGE,xlab = "Ground cover (%)" ,ylab = "Forest age"
For the sites with very high ground cover, they still have a range of different forest age values. So that suggests that forest age might be helpful at trying to understand why these sites with similar ground cover have such high variability in salamander counts.
plot ($ FORESTAGE,$ SALAMAN,ylab = "Salamander count" ,xlab = "Forest age"
But we can see there isn’t much of a relationship between forest age and salamander count, so the forest age just isn’t that useful for predicting how many salamanders we’ll find, or at least all of the variability in salamander counts that’s explained by forest age is already explained by ground cover. We can fit a model with just the forest age to test how predictive forest age is by itself.
<- rethinking:: ulam (alist (~ dpois (lambda),log (lambda) <- a + bf * fa,~ dnorm (3 , 0.5 ),~ dnorm (0 , 0.2 )data = s_dat,chains = 4 , cores = 4 ,log_lik = TRUE
In file included from stan/src/stan/model/model_header.hpp:5:
stan/src/stan/model/model_base_crtp.hpp:205:8: warning: 'void stan::model::model_base_crtp<M>::write_array(stan::rng_t&, std::vector<double>&, std::vector<int>&, std::vector<double>&, bool, bool, std::ostream*) const [with M = ulam_cmdstanr_38c3460d7f0e749042135cb08e5fea5a_model_namespace::ulam_cmdstanr_38c3460d7f0e749042135cb08e5fea5a_model; stan::rng_t = boost::random::mixmax_engine<17, 36, 0>; std::ostream = std::basic_ostream<char>]' was hidden [-Woverloaded-virtual=]
205 | void write_array(stan::rng_t& rng, std::vector<double>& theta,
| ^~~~~~~~~~~
C:/Users/Zane/AppData/Local/Temp/RtmpSCWF6a/model-305c63b628b3.hpp:460: note: by 'ulam_cmdstanr_38c3460d7f0e749042135cb08e5fea5a_model_namespace::ulam_cmdstanr_38c3460d7f0e749042135cb08e5fea5a_model::write_array'
460 | write_array(RNG& base_rng, std::vector<double>& params_r, std::vector<int>&
stan/src/stan/model/model_base_crtp.hpp:136:8: warning: 'void stan::model::model_base_crtp<M>::write_array(stan::rng_t&, Eigen::VectorXd&, Eigen::VectorXd&, bool, bool, std::ostream*) const [with M = ulam_cmdstanr_38c3460d7f0e749042135cb08e5fea5a_model_namespace::ulam_cmdstanr_38c3460d7f0e749042135cb08e5fea5a_model; stan::rng_t = boost::random::mixmax_engine<17, 36, 0>; Eigen::VectorXd = Eigen::Matrix<double, -1, 1>; std::ostream = std::basic_ostream<char>]' was hidden [-Woverloaded-virtual=]
136 | void write_array(stan::rng_t& rng, Eigen::VectorXd& theta,
| ^~~~~~~~~~~
C:/Users/Zane/AppData/Local/Temp/RtmpSCWF6a/model-305c63b628b3.hpp:460: note: by 'ulam_cmdstanr_38c3460d7f0e749042135cb08e5fea5a_model_namespace::ulam_cmdstanr_38c3460d7f0e749042135cb08e5fea5a_model::write_array'
460 | write_array(RNG& base_rng, std::vector<double>& params_r, std::vector<int>&
Running MCMC with 4 parallel chains, with 1 thread(s) per chain...
Chain 1 Iteration: 1 / 1000 [ 0%] (Warmup)
Chain 1 Iteration: 100 / 1000 [ 10%] (Warmup)
Chain 1 Iteration: 200 / 1000 [ 20%] (Warmup)
Chain 1 Iteration: 300 / 1000 [ 30%] (Warmup)
Chain 1 Iteration: 400 / 1000 [ 40%] (Warmup)
Chain 1 Iteration: 500 / 1000 [ 50%] (Warmup)
Chain 1 Iteration: 501 / 1000 [ 50%] (Sampling)
Chain 1 Iteration: 600 / 1000 [ 60%] (Sampling)
Chain 1 Iteration: 700 / 1000 [ 70%] (Sampling)
Chain 1 Iteration: 800 / 1000 [ 80%] (Sampling)
Chain 1 Iteration: 900 / 1000 [ 90%] (Sampling)
Chain 1 Iteration: 1000 / 1000 [100%] (Sampling)
Chain 2 Iteration: 1 / 1000 [ 0%] (Warmup)
Chain 2 Iteration: 100 / 1000 [ 10%] (Warmup)
Chain 2 Iteration: 200 / 1000 [ 20%] (Warmup)
Chain 2 Iteration: 300 / 1000 [ 30%] (Warmup)
Chain 2 Iteration: 400 / 1000 [ 40%] (Warmup)
Chain 2 Iteration: 500 / 1000 [ 50%] (Warmup)
Chain 2 Iteration: 501 / 1000 [ 50%] (Sampling)
Chain 2 Iteration: 600 / 1000 [ 60%] (Sampling)
Chain 2 Iteration: 700 / 1000 [ 70%] (Sampling)
Chain 2 Iteration: 800 / 1000 [ 80%] (Sampling)
Chain 2 Iteration: 900 / 1000 [ 90%] (Sampling)
Chain 2 Iteration: 1000 / 1000 [100%] (Sampling)
Chain 3 Iteration: 1 / 1000 [ 0%] (Warmup)
Chain 3 Iteration: 100 / 1000 [ 10%] (Warmup)
Chain 3 Iteration: 200 / 1000 [ 20%] (Warmup)
Chain 3 Iteration: 300 / 1000 [ 30%] (Warmup)
Chain 3 Iteration: 400 / 1000 [ 40%] (Warmup)
Chain 3 Iteration: 500 / 1000 [ 50%] (Warmup)
Chain 3 Iteration: 501 / 1000 [ 50%] (Sampling)
Chain 3 Iteration: 600 / 1000 [ 60%] (Sampling)
Chain 3 Iteration: 700 / 1000 [ 70%] (Sampling)
Chain 3 Iteration: 800 / 1000 [ 80%] (Sampling)
Chain 4 Iteration: 1 / 1000 [ 0%] (Warmup)
Chain 4 Iteration: 100 / 1000 [ 10%] (Warmup)
Chain 4 Iteration: 200 / 1000 [ 20%] (Warmup)
Chain 4 Iteration: 300 / 1000 [ 30%] (Warmup)
Chain 4 Iteration: 400 / 1000 [ 40%] (Warmup)
Chain 4 Iteration: 500 / 1000 [ 50%] (Warmup)
Chain 4 Iteration: 501 / 1000 [ 50%] (Sampling)
Chain 4 Iteration: 600 / 1000 [ 60%] (Sampling)
Chain 4 Iteration: 700 / 1000 [ 70%] (Sampling)
Chain 1 finished in 0.1 seconds.
Chain 2 finished in 0.1 seconds.
Chain 3 Iteration: 900 / 1000 [ 90%] (Sampling)
Chain 3 Iteration: 1000 / 1000 [100%] (Sampling)
Chain 3 finished in 0.1 seconds.
Chain 4 Iteration: 800 / 1000 [ 80%] (Sampling)
Chain 4 Iteration: 900 / 1000 [ 90%] (Sampling)
Chain 4 Iteration: 1000 / 1000 [100%] (Sampling)
Chain 4 finished in 0.1 seconds.
All 4 chains finished successfully.
Mean chain execution time: 0.1 seconds.
Total execution time: 0.3 seconds.
:: precis (m_11h3_d)
mean sd 5.5% 94.5% rhat ess_bulk
a 0.9156406 0.09496459 0.7613632 1.0636813 0.9998592 1179.993
bf 0.2995171 0.07471753 0.1828759 0.4221297 1.0022846 1198.815
So in isolation, the forest age is predictive. But it doesn’t seem to tell us anything we don’t already know from groundcover. So perhaps there are other differences between sites that we haven’t measured, or in old forests with high groundcover, there’s just a lot of inherent variability in salamander dispersal. Depending on how close the sites are, looking at spatial correlation between sites might explain a lot too.
11H4
In this question, we want to model the total and direct causal effects of gender of applicant on receiving scientific funding in an NWO grant application.
data ("NWOGrants" , package = "rethinking" )<- list (d = factor (NWOGrants$ discipline) |> forcats:: fct_inorder () |> as.integer (),g = ifelse (NWOGrants$ gender == "m" , 0 , 1 ),y = NWOGrants$ awards,n = NWOGrants$ applications
We want to consider discipline as a mediator of the effect of gender on application awards. There are no other confounders in the dataset, so for now we’ll assume we don’t have any, but we’ll have to touch on this in our causal interpretations. So to estimate the total and direct causal effects of gender we should estimate two models. One where gender is the only predictor, and one where gender and discipline are both in the model.
<- rethinking:: ulam (alist (~ dbinom (n, p),logit (p) <- a + bg * g,~ dnorm (0 , 1 ),~ dnorm (0 , 0.5 )data = nwo,cores = 4 , chains = 4
In file included from stan/src/stan/model/model_header.hpp:5:
stan/src/stan/model/model_base_crtp.hpp:205:8: warning: 'void stan::model::model_base_crtp<M>::write_array(stan::rng_t&, std::vector<double>&, std::vector<int>&, std::vector<double>&, bool, bool, std::ostream*) const [with M = ulam_cmdstanr_cc2467483e8f8bb804920aaf8932ded4_model_namespace::ulam_cmdstanr_cc2467483e8f8bb804920aaf8932ded4_model; stan::rng_t = boost::random::mixmax_engine<17, 36, 0>; std::ostream = std::basic_ostream<char>]' was hidden [-Woverloaded-virtual=]
205 | void write_array(stan::rng_t& rng, std::vector<double>& theta,
| ^~~~~~~~~~~
C:/Users/Zane/AppData/Local/Temp/RtmpSCWF6a/model-305c700441e.hpp:376: note: by 'ulam_cmdstanr_cc2467483e8f8bb804920aaf8932ded4_model_namespace::ulam_cmdstanr_cc2467483e8f8bb804920aaf8932ded4_model::write_array'
376 | write_array(RNG& base_rng, std::vector<double>& params_r, std::vector<int>&
stan/src/stan/model/model_base_crtp.hpp:136:8: warning: 'void stan::model::model_base_crtp<M>::write_array(stan::rng_t&, Eigen::VectorXd&, Eigen::VectorXd&, bool, bool, std::ostream*) const [with M = ulam_cmdstanr_cc2467483e8f8bb804920aaf8932ded4_model_namespace::ulam_cmdstanr_cc2467483e8f8bb804920aaf8932ded4_model; stan::rng_t = boost::random::mixmax_engine<17, 36, 0>; Eigen::VectorXd = Eigen::Matrix<double, -1, 1>; std::ostream = std::basic_ostream<char>]' was hidden [-Woverloaded-virtual=]
136 | void write_array(stan::rng_t& rng, Eigen::VectorXd& theta,
| ^~~~~~~~~~~
C:/Users/Zane/AppData/Local/Temp/RtmpSCWF6a/model-305c700441e.hpp:376: note: by 'ulam_cmdstanr_cc2467483e8f8bb804920aaf8932ded4_model_namespace::ulam_cmdstanr_cc2467483e8f8bb804920aaf8932ded4_model::write_array'
376 | write_array(RNG& base_rng, std::vector<double>& params_r, std::vector<int>&
Running MCMC with 4 parallel chains, with 1 thread(s) per chain...
Chain 1 Iteration: 1 / 1000 [ 0%] (Warmup)
Chain 1 Iteration: 100 / 1000 [ 10%] (Warmup)
Chain 1 Iteration: 200 / 1000 [ 20%] (Warmup)
Chain 1 Iteration: 300 / 1000 [ 30%] (Warmup)
Chain 1 Iteration: 400 / 1000 [ 40%] (Warmup)
Chain 1 Iteration: 500 / 1000 [ 50%] (Warmup)
Chain 1 Iteration: 501 / 1000 [ 50%] (Sampling)
Chain 1 Iteration: 600 / 1000 [ 60%] (Sampling)
Chain 1 Iteration: 700 / 1000 [ 70%] (Sampling)
Chain 1 Iteration: 800 / 1000 [ 80%] (Sampling)
Chain 1 Iteration: 900 / 1000 [ 90%] (Sampling)
Chain 1 Iteration: 1000 / 1000 [100%] (Sampling)
Chain 2 Iteration: 1 / 1000 [ 0%] (Warmup)
Chain 2 Iteration: 100 / 1000 [ 10%] (Warmup)
Chain 2 Iteration: 200 / 1000 [ 20%] (Warmup)
Chain 2 Iteration: 300 / 1000 [ 30%] (Warmup)
Chain 2 Iteration: 400 / 1000 [ 40%] (Warmup)
Chain 2 Iteration: 500 / 1000 [ 50%] (Warmup)
Chain 2 Iteration: 501 / 1000 [ 50%] (Sampling)
Chain 2 Iteration: 600 / 1000 [ 60%] (Sampling)
Chain 2 Iteration: 700 / 1000 [ 70%] (Sampling)
Chain 2 Iteration: 800 / 1000 [ 80%] (Sampling)
Chain 2 Iteration: 900 / 1000 [ 90%] (Sampling)
Chain 2 Iteration: 1000 / 1000 [100%] (Sampling)
Chain 3 Iteration: 1 / 1000 [ 0%] (Warmup)
Chain 3 Iteration: 100 / 1000 [ 10%] (Warmup)
Chain 3 Iteration: 200 / 1000 [ 20%] (Warmup)
Chain 3 Iteration: 300 / 1000 [ 30%] (Warmup)
Chain 3 Iteration: 400 / 1000 [ 40%] (Warmup)
Chain 3 Iteration: 500 / 1000 [ 50%] (Warmup)
Chain 3 Iteration: 501 / 1000 [ 50%] (Sampling)
Chain 3 Iteration: 600 / 1000 [ 60%] (Sampling)
Chain 3 Iteration: 700 / 1000 [ 70%] (Sampling)
Chain 3 Iteration: 800 / 1000 [ 80%] (Sampling)
Chain 3 Iteration: 900 / 1000 [ 90%] (Sampling)
Chain 3 Iteration: 1000 / 1000 [100%] (Sampling)
Chain 4 Iteration: 1 / 1000 [ 0%] (Warmup)
Chain 4 Iteration: 100 / 1000 [ 10%] (Warmup)
Chain 4 Iteration: 200 / 1000 [ 20%] (Warmup)
Chain 4 Iteration: 300 / 1000 [ 30%] (Warmup)
Chain 4 Iteration: 400 / 1000 [ 40%] (Warmup)
Chain 4 Iteration: 500 / 1000 [ 50%] (Warmup)
Chain 4 Iteration: 501 / 1000 [ 50%] (Sampling)
Chain 4 Iteration: 600 / 1000 [ 60%] (Sampling)
Chain 4 Iteration: 700 / 1000 [ 70%] (Sampling)
Chain 4 Iteration: 800 / 1000 [ 80%] (Sampling)
Chain 4 Iteration: 900 / 1000 [ 90%] (Sampling)
Chain 4 Iteration: 1000 / 1000 [100%] (Sampling)
Chain 1 finished in 0.0 seconds.
Chain 2 finished in 0.0 seconds.
Chain 3 finished in 0.0 seconds.
Chain 4 finished in 0.0 seconds.
All 4 chains finished successfully.
Mean chain execution time: 0.0 seconds.
Total execution time: 0.3 seconds.
<- rethinking:: ulam (alist (~ dbinom (n, p),logit (p) <- bg * g + bd[d],~ dnorm (0 , 0.5 ),~ dnorm (0 , 0.5 )data = nwo,cores = 4 , chains = 4
In file included from stan/src/stan/model/model_header.hpp:5:
stan/src/stan/model/model_base_crtp.hpp:205:8: warning: 'void stan::model::model_base_crtp<M>::write_array(stan::rng_t&, std::vector<double>&, std::vector<int>&, std::vector<double>&, bool, bool, std::ostream*) const [with M = ulam_cmdstanr_2274787348422e0cdb2b2141e5815653_model_namespace::ulam_cmdstanr_2274787348422e0cdb2b2141e5815653_model; stan::rng_t = boost::random::mixmax_engine<17, 36, 0>; std::ostream = std::basic_ostream<char>]' was hidden [-Woverloaded-virtual=]
205 | void write_array(stan::rng_t& rng, std::vector<double>& theta,
| ^~~~~~~~~~~
C:/Users/Zane/AppData/Local/Temp/RtmpSCWF6a/model-305c18236db5.hpp:401: note: by 'ulam_cmdstanr_2274787348422e0cdb2b2141e5815653_model_namespace::ulam_cmdstanr_2274787348422e0cdb2b2141e5815653_model::write_array'
401 | write_array(RNG& base_rng, std::vector<double>& params_r, std::vector<int>&
stan/src/stan/model/model_base_crtp.hpp:136:8: warning: 'void stan::model::model_base_crtp<M>::write_array(stan::rng_t&, Eigen::VectorXd&, Eigen::VectorXd&, bool, bool, std::ostream*) const [with M = ulam_cmdstanr_2274787348422e0cdb2b2141e5815653_model_namespace::ulam_cmdstanr_2274787348422e0cdb2b2141e5815653_model; stan::rng_t = boost::random::mixmax_engine<17, 36, 0>; Eigen::VectorXd = Eigen::Matrix<double, -1, 1>; std::ostream = std::basic_ostream<char>]' was hidden [-Woverloaded-virtual=]
136 | void write_array(stan::rng_t& rng, Eigen::VectorXd& theta,
| ^~~~~~~~~~~
C:/Users/Zane/AppData/Local/Temp/RtmpSCWF6a/model-305c18236db5.hpp:401: note: by 'ulam_cmdstanr_2274787348422e0cdb2b2141e5815653_model_namespace::ulam_cmdstanr_2274787348422e0cdb2b2141e5815653_model::write_array'
401 | write_array(RNG& base_rng, std::vector<double>& params_r, std::vector<int>&
Running MCMC with 4 parallel chains, with 1 thread(s) per chain...
Chain 1 Iteration: 1 / 1000 [ 0%] (Warmup)
Chain 1 Iteration: 100 / 1000 [ 10%] (Warmup)
Chain 1 Iteration: 200 / 1000 [ 20%] (Warmup)
Chain 1 Iteration: 300 / 1000 [ 30%] (Warmup)
Chain 1 Iteration: 400 / 1000 [ 40%] (Warmup)
Chain 1 Iteration: 500 / 1000 [ 50%] (Warmup)
Chain 1 Iteration: 501 / 1000 [ 50%] (Sampling)
Chain 1 Iteration: 600 / 1000 [ 60%] (Sampling)
Chain 1 Iteration: 700 / 1000 [ 70%] (Sampling)
Chain 1 Iteration: 800 / 1000 [ 80%] (Sampling)
Chain 1 Iteration: 900 / 1000 [ 90%] (Sampling)
Chain 1 Iteration: 1000 / 1000 [100%] (Sampling)
Chain 2 Iteration: 1 / 1000 [ 0%] (Warmup)
Chain 2 Iteration: 100 / 1000 [ 10%] (Warmup)
Chain 2 Iteration: 200 / 1000 [ 20%] (Warmup)
Chain 2 Iteration: 300 / 1000 [ 30%] (Warmup)
Chain 2 Iteration: 400 / 1000 [ 40%] (Warmup)
Chain 2 Iteration: 500 / 1000 [ 50%] (Warmup)
Chain 2 Iteration: 501 / 1000 [ 50%] (Sampling)
Chain 2 Iteration: 600 / 1000 [ 60%] (Sampling)
Chain 2 Iteration: 700 / 1000 [ 70%] (Sampling)
Chain 2 Iteration: 800 / 1000 [ 80%] (Sampling)
Chain 2 Iteration: 900 / 1000 [ 90%] (Sampling)
Chain 2 Iteration: 1000 / 1000 [100%] (Sampling)
Chain 3 Iteration: 1 / 1000 [ 0%] (Warmup)
Chain 3 Iteration: 100 / 1000 [ 10%] (Warmup)
Chain 3 Iteration: 200 / 1000 [ 20%] (Warmup)
Chain 3 Iteration: 300 / 1000 [ 30%] (Warmup)
Chain 3 Iteration: 400 / 1000 [ 40%] (Warmup)
Chain 3 Iteration: 500 / 1000 [ 50%] (Warmup)
Chain 3 Iteration: 501 / 1000 [ 50%] (Sampling)
Chain 3 Iteration: 600 / 1000 [ 60%] (Sampling)
Chain 3 Iteration: 700 / 1000 [ 70%] (Sampling)
Chain 3 Iteration: 800 / 1000 [ 80%] (Sampling)
Chain 3 Iteration: 900 / 1000 [ 90%] (Sampling)
Chain 3 Iteration: 1000 / 1000 [100%] (Sampling)
Chain 4 Iteration: 1 / 1000 [ 0%] (Warmup)
Chain 4 Iteration: 100 / 1000 [ 10%] (Warmup)
Chain 4 Iteration: 200 / 1000 [ 20%] (Warmup)
Chain 4 Iteration: 300 / 1000 [ 30%] (Warmup)
Chain 4 Iteration: 400 / 1000 [ 40%] (Warmup)
Chain 4 Iteration: 500 / 1000 [ 50%] (Warmup)
Chain 4 Iteration: 501 / 1000 [ 50%] (Sampling)
Chain 4 Iteration: 600 / 1000 [ 60%] (Sampling)
Chain 4 Iteration: 700 / 1000 [ 70%] (Sampling)
Chain 4 Iteration: 800 / 1000 [ 80%] (Sampling)
Chain 4 Iteration: 900 / 1000 [ 90%] (Sampling)
Chain 4 Iteration: 1000 / 1000 [100%] (Sampling)
Chain 1 finished in 0.1 seconds.
Chain 2 finished in 0.1 seconds.
Chain 3 finished in 0.1 seconds.
Chain 4 finished in 0.1 seconds.
All 4 chains finished successfully.
Mean chain execution time: 0.1 seconds.
Total execution time: 0.3 seconds.
First we’ll look at the total causal effect, from the model that only includes an effect for gender. When we take a look at the coefficients, we can see that we’re pretty confident in a small negative effect of gender on application probability. Specifically, the OR estimate is \(0.81\) , indicating that women have \(0.8\) times the odds of getting a grant awarded than a man overall.
:: precis (m_11h4_1, depth = 2 )
mean sd 5.5% 94.5% rhat ess_bulk
a -1.5343019 0.06467142 -1.6381804 -1.43376020 1.003695 825.1131
bg -0.2033113 0.10108333 -0.3653252 -0.04041632 1.002544 858.9978
What we really want to do is estimate the change between a man and a woman applying for the same grant, regardless of discipline, so we need to get predictions for that and subtract.
<- rethinking:: link (m_11h4_1, data = data.frame (g = c (0 , 1 )))# Contrast for men (1) - women (2) <- post[,1 ] - post[,2 ]<- mean (contr_post)<- rethinking:: PI (contr_post)paste0 (round (contr_mean, 2 ), " (" , round (contr_pi[1 ], 2 ), ", " ,round (contr_pi[2 ], 2 ), ")"
So we can see that the total causal effect of gender on application status across all disciplines is that a man is \(3\%\) more likely to receive an application than a woman who submits the exact same application. So that’s actually quite a small effect on the scale we care about, whereas an OR of \(0.8\) suggests that there might be quite a large disparity. On the other hand, however, if we look at the dataset we can see that only about \(19\%\) of all applications received awards, so a small difference in award chance could be very meaningful.
Now let’s look at the direct causal effect of gender when we also control for discipline as a mediator. First let’s look at the coefficients. For this model, I included an effect of being female, and an index-coded effect of discipline. I also left out the overall intercept since it’s not identifiable with an intercept effect for each discipline.
:: precis (m_11h4_2, depth = 2 )
mean sd 5.5% 94.5% rhat ess_bulk
bg -0.3035044 0.0985806 -0.4592999 -0.1497102 1.004233 1409.300
bd[1] -0.8192188 0.1961072 -1.1392042 -0.5146626 1.002648 2406.387
bd[2] -1.1606118 0.1706895 -1.4353328 -0.8933208 1.000810 2359.080
bd[3] -0.8078297 0.2270755 -1.1630780 -0.4512975 1.003261 2384.151
bd[4] -1.4138543 0.1342582 -1.6295381 -1.1950501 1.000583 2351.405
bd[5] -1.3618201 0.1580670 -1.6269593 -1.1091490 1.000115 2729.508
bd[6] -1.3477174 0.1797236 -1.6399531 -1.0649567 1.003235 2360.827
bd[7] -1.1757195 0.1489185 -1.4175831 -0.9391356 1.001505 1690.293
bd[8] -1.6606674 0.1023214 -1.8257840 -1.4960926 1.001779 1715.406
bd[9] -1.5100828 0.1279871 -1.7190608 -1.3029240 1.000796 2038.353
After accounting for the discipline in our model, we get that the OR for gender is \(0.74\) , slightly lower than our previous model, but well within the credibility limits of the previous estimate. Let’s get an estimate of how much gender affects award rate in each discipline.
<- expand.grid (g = c (0 , 1 ), d = 1 : 9 )<- rethinking:: link (data = pred_data<- data.frame (d = factor (NWOGrants$ discipline) |> forcats:: fct_inorder () |> as.integer (),discipline = NWOGrants$ discipline|> :: distinct ()<- cbind (t (post) |> ` colnames<- ` (1 : nrow (post))|> :: pivot_longer (- c (g, d), names_to = "draw" , values_to = "sample" ) |> :: summarize (:: mean_qi (sample, .width = 0.89 ),.by = c (g, d)|> :: left_join (dpt_lookups, by = "d" ) |> :: select (- d) |> :: mutate (g = factor (ifelse (g == 0 , "Man" , "Woman" )))<- c ("Chem S." , "Phys S." , "Phys" , "Hum" , "Tech" , "Int" , "Earth S." ,"Soc S." , "Med S." )<- 0.1 plot (x = 1 : 9 - k,y = subset (tidy_post, g == "Man" )$ y,xlab = "Discipline" ,xaxt = "n" ,ylab = "Chance of award acceptance" ,ylim = c (0 , 0.5 ),xlim = c (1 - k, 9 + k),col = "dodgerblue" arrows (x0 = 1 : 9 - k,x = 1 : 9 - k,y0 = subset (tidy_post, g == "Man" )$ ymin,y = subset (tidy_post, g == "Man" )$ ymax,length = 0.05 ,angle = 90 ,code = 3 ,col = "dodgerblue" points (x = 1 : 9 + k,y = subset (tidy_post, g == "Woman" )$ y,col = "darkorange" arrows (x0 = 1 : 9 + k,x = 1 : 9 + k,y0 = subset (tidy_post, g == "Woman" )$ ymin,y = subset (tidy_post, g == "Woman" )$ ymax,length = 0.05 ,angle = 90 ,code = 3 ,col = "darkorange" axis (1 , at = 1 : 9 , labels = labs)legend ("topright" ,lty = 1 , pch = 1 , col = c ("dodgerblue" , "darkorange" ),legend = c ("Men" , "Women" )
If we average across all disciplies, after accounting for the different baseline application rates between genders in each, we can see that woman were still less likely to get awards, with a difference of about 3% to 5% per discipline.
This is different from the conclusion that McElreath got, but I don’t really think I did anything wrong so I’m not sure I’m inclined to change anything. My model sampled more efficiently than the one in the solutions manual and doesn’t have the extra unnecessary parameter, so I’m tempted to conclude that I can trust my results, especially since I’m looking at the posterior predictions on the link scale.
I wasn’t sure what was causing this discrepancy other than McElreath’s sampling issues, so I double checked the relationship between the proportion of female applicants and awards accepted per department.
<- |> :: summarise (applications = sum (applications),awards = sum (awards),p = awards / applications,.by = discipline<- |> :: select (- awards) |> :: pivot_wider (names_from = gender, values_from = applications) |> :: mutate (p = f / (f + m)plot ($ p, c2$ p,xlab = "Prop. awards accepted" ,ylab = "Prop. female applicants"
We can see that, on average, more women do apply to less-funded categories. But my results suggest that even after taking that into account, a man was \(5\%\) more likely to receive an award than a woman. Maybe if we fit a model with an interaction it will reveal more – our current model doesn’t allow for some disciplines to be better for woman than men, it only allows one overall effect for gender.
<- rethinking:: ulam (alist (~ dbinom (n, p),logit (p) <- bg * g + bd[d] + k[d] * bg,~ dnorm (0 , 0.5 ),~ dnorm (0 , 0.5 ),~ dnorm (0 , 0.5 )data = nwo,cores = 4 , chains = 4
In file included from stan/src/stan/model/model_header.hpp:5:
stan/src/stan/model/model_base_crtp.hpp:205:8: warning: 'void stan::model::model_base_crtp<M>::write_array(stan::rng_t&, std::vector<double>&, std::vector<int>&, std::vector<double>&, bool, bool, std::ostream*) const [with M = ulam_cmdstanr_7c42979430a5edd6976e398176487f18_model_namespace::ulam_cmdstanr_7c42979430a5edd6976e398176487f18_model; stan::rng_t = boost::random::mixmax_engine<17, 36, 0>; std::ostream = std::basic_ostream<char>]' was hidden [-Woverloaded-virtual=]
205 | void write_array(stan::rng_t& rng, std::vector<double>& theta,
| ^~~~~~~~~~~
C:/Users/Zane/AppData/Local/Temp/RtmpSCWF6a/model-305c74174f19.hpp:456: note: by 'ulam_cmdstanr_7c42979430a5edd6976e398176487f18_model_namespace::ulam_cmdstanr_7c42979430a5edd6976e398176487f18_model::write_array'
456 | write_array(RNG& base_rng, std::vector<double>& params_r, std::vector<int>&
stan/src/stan/model/model_base_crtp.hpp:136:8: warning: 'void stan::model::model_base_crtp<M>::write_array(stan::rng_t&, Eigen::VectorXd&, Eigen::VectorXd&, bool, bool, std::ostream*) const [with M = ulam_cmdstanr_7c42979430a5edd6976e398176487f18_model_namespace::ulam_cmdstanr_7c42979430a5edd6976e398176487f18_model; stan::rng_t = boost::random::mixmax_engine<17, 36, 0>; Eigen::VectorXd = Eigen::Matrix<double, -1, 1>; std::ostream = std::basic_ostream<char>]' was hidden [-Woverloaded-virtual=]
136 | void write_array(stan::rng_t& rng, Eigen::VectorXd& theta,
| ^~~~~~~~~~~
C:/Users/Zane/AppData/Local/Temp/RtmpSCWF6a/model-305c74174f19.hpp:456: note: by 'ulam_cmdstanr_7c42979430a5edd6976e398176487f18_model_namespace::ulam_cmdstanr_7c42979430a5edd6976e398176487f18_model::write_array'
456 | write_array(RNG& base_rng, std::vector<double>& params_r, std::vector<int>&
Running MCMC with 4 parallel chains, with 1 thread(s) per chain...
Chain 1 Iteration: 1 / 1000 [ 0%] (Warmup)
Chain 1 Iteration: 100 / 1000 [ 10%] (Warmup)
Chain 1 Iteration: 200 / 1000 [ 20%] (Warmup)
Chain 1 Iteration: 300 / 1000 [ 30%] (Warmup)
Chain 1 Iteration: 400 / 1000 [ 40%] (Warmup)
Chain 1 Iteration: 500 / 1000 [ 50%] (Warmup)
Chain 1 Iteration: 501 / 1000 [ 50%] (Sampling)
Chain 1 Iteration: 600 / 1000 [ 60%] (Sampling)
Chain 2 Iteration: 1 / 1000 [ 0%] (Warmup)
Chain 2 Iteration: 100 / 1000 [ 10%] (Warmup)
Chain 2 Iteration: 200 / 1000 [ 20%] (Warmup)
Chain 2 Iteration: 300 / 1000 [ 30%] (Warmup)
Chain 2 Iteration: 400 / 1000 [ 40%] (Warmup)
Chain 3 Iteration: 1 / 1000 [ 0%] (Warmup)
Chain 3 Iteration: 100 / 1000 [ 10%] (Warmup)
Chain 3 Iteration: 200 / 1000 [ 20%] (Warmup)
Chain 3 Iteration: 300 / 1000 [ 30%] (Warmup)
Chain 3 Iteration: 400 / 1000 [ 40%] (Warmup)
Chain 3 Iteration: 500 / 1000 [ 50%] (Warmup)
Chain 3 Iteration: 501 / 1000 [ 50%] (Sampling)
Chain 4 Iteration: 1 / 1000 [ 0%] (Warmup)
Chain 4 Iteration: 100 / 1000 [ 10%] (Warmup)
Chain 4 Iteration: 200 / 1000 [ 20%] (Warmup)
Chain 4 Iteration: 300 / 1000 [ 30%] (Warmup)
Chain 4 Iteration: 400 / 1000 [ 40%] (Warmup)
Chain 1 Iteration: 700 / 1000 [ 70%] (Sampling)
Chain 1 Iteration: 800 / 1000 [ 80%] (Sampling)
Chain 1 Iteration: 900 / 1000 [ 90%] (Sampling)
Chain 1 Iteration: 1000 / 1000 [100%] (Sampling)
Chain 1 finished in 0.2 seconds.
Chain 2 Iteration: 500 / 1000 [ 50%] (Warmup)
Chain 2 Iteration: 501 / 1000 [ 50%] (Sampling)
Chain 2 Iteration: 600 / 1000 [ 60%] (Sampling)
Chain 2 Iteration: 700 / 1000 [ 70%] (Sampling)
Chain 2 Iteration: 800 / 1000 [ 80%] (Sampling)
Chain 2 Iteration: 900 / 1000 [ 90%] (Sampling)
Chain 2 Iteration: 1000 / 1000 [100%] (Sampling)
Chain 2 finished in 0.2 seconds.
Chain 3 Iteration: 600 / 1000 [ 60%] (Sampling)
Chain 3 Iteration: 700 / 1000 [ 70%] (Sampling)
Chain 3 Iteration: 800 / 1000 [ 80%] (Sampling)
Chain 3 Iteration: 900 / 1000 [ 90%] (Sampling)
Chain 3 Iteration: 1000 / 1000 [100%] (Sampling)
Chain 3 finished in 0.2 seconds.
Chain 4 Iteration: 500 / 1000 [ 50%] (Warmup)
Chain 4 Iteration: 501 / 1000 [ 50%] (Sampling)
Chain 4 Iteration: 600 / 1000 [ 60%] (Sampling)
Chain 4 Iteration: 700 / 1000 [ 70%] (Sampling)
Chain 4 Iteration: 800 / 1000 [ 80%] (Sampling)
Chain 4 Iteration: 900 / 1000 [ 90%] (Sampling)
Chain 4 Iteration: 1000 / 1000 [100%] (Sampling)
Chain 4 finished in 0.2 seconds.
All 4 chains finished successfully.
Mean chain execution time: 0.2 seconds.
Total execution time: 0.3 seconds.
:: precis (m_11h4_3, depth = 2 )
mean sd 5.5% 94.5% rhat ess_bulk
bg -0.4248661 0.1047389 -0.5839973 -0.2543484 1.0033646 1187.142
bd[1] -0.6752043 0.2623479 -1.0785866 -0.2448724 1.0034604 2091.338
bd[2] -0.9903476 0.2497958 -1.3821000 -0.5855345 1.0003766 2001.667
bd[3] -0.6831556 0.2817839 -1.1377438 -0.2371330 1.0040745 2364.392
bd[4] -1.1713506 0.2494143 -1.5548050 -0.7516570 1.0034577 1446.784
bd[5] -1.1530403 0.2518371 -1.5543321 -0.7287779 1.0046178 1820.810
bd[6] -1.1247111 0.2730646 -1.5418504 -0.6732695 1.0029530 1642.888
bd[7] -0.9610122 0.2537695 -1.3477093 -0.5439327 1.0029153 1835.838
bd[8] -1.3687827 0.2472884 -1.7292831 -0.9632739 1.0026561 1435.781
bd[9] -1.2433149 0.2527280 -1.6142368 -0.8381837 1.0023990 1435.511
k[1] 0.2867909 0.4775706 -0.4679153 1.0345954 1.0053830 2487.453
k[2] 0.4074244 0.4646149 -0.3304590 1.1501311 0.9994584 2245.661
k[3] 0.2862592 0.4724993 -0.4823118 1.0562627 1.0033355 2301.792
k[4] 0.4829170 0.4741066 -0.2596633 1.2309973 1.0015245 1751.698
k[5] 0.4727853 0.4609300 -0.2634229 1.2286066 1.0016932 2195.121
k[6] 0.4725448 0.4719456 -0.2728809 1.2341925 1.0014951 2037.686
k[7] 0.4071437 0.4711221 -0.3463571 1.1294235 1.0041017 2073.023
k[8] 0.5694931 0.4613258 -0.1848281 1.3089253 1.0030680 1825.086
k[9] 0.5176680 0.4615534 -0.2048439 1.2549287 1.0014863 1838.670
Still no real sampling issues, probably cause I dummy coded the effect of \(g\) so we don’t have an extra intercept term. It’s tempting to conclude that the effect of \(bg\) is larger now, but we can see that some of the \(k\) terms will cancel this out in specific disciplines – except all the \(k\) terms have pretty huge uncertainties. I had the same basic results with this model as the previous one (not shown for brevity), cause I think it forces the overall effect of gender to be negative still. So instead I decided to fit a more flexible model that allows each combination of gender and discipline to have its own estimated log-odds.
$ g2 <- nwo$ g + 1 <- rethinking:: ulam (alist (~ dbinom (n, p),logit (p) <- a[d, g2],: a ~ dnorm (0 , 0.25 )data = nwo,cores = 4 , chains = 4
In file included from stan/src/stan/model/model_header.hpp:5:
stan/src/stan/model/model_base_crtp.hpp:205:8: warning: 'void stan::model::model_base_crtp<M>::write_array(stan::rng_t&, std::vector<double>&, std::vector<int>&, std::vector<double>&, bool, bool, std::ostream*) const [with M = ulam_cmdstanr_4fe7673b04feaf50c3cdcaf9c5088fde_model_namespace::ulam_cmdstanr_4fe7673b04feaf50c3cdcaf9c5088fde_model; stan::rng_t = boost::random::mixmax_engine<17, 36, 0>; std::ostream = std::basic_ostream<char>]' was hidden [-Woverloaded-virtual=]
205 | void write_array(stan::rng_t& rng, std::vector<double>& theta,
| ^~~~~~~~~~~
C:/Users/Zane/AppData/Local/Temp/RtmpSCWF6a/model-305c763066bb.hpp:396: note: by 'ulam_cmdstanr_4fe7673b04feaf50c3cdcaf9c5088fde_model_namespace::ulam_cmdstanr_4fe7673b04feaf50c3cdcaf9c5088fde_model::write_array'
396 | write_array(RNG& base_rng, std::vector<double>& params_r, std::vector<int>&
stan/src/stan/model/model_base_crtp.hpp:136:8: warning: 'void stan::model::model_base_crtp<M>::write_array(stan::rng_t&, Eigen::VectorXd&, Eigen::VectorXd&, bool, bool, std::ostream*) const [with M = ulam_cmdstanr_4fe7673b04feaf50c3cdcaf9c5088fde_model_namespace::ulam_cmdstanr_4fe7673b04feaf50c3cdcaf9c5088fde_model; stan::rng_t = boost::random::mixmax_engine<17, 36, 0>; Eigen::VectorXd = Eigen::Matrix<double, -1, 1>; std::ostream = std::basic_ostream<char>]' was hidden [-Woverloaded-virtual=]
136 | void write_array(stan::rng_t& rng, Eigen::VectorXd& theta,
| ^~~~~~~~~~~
C:/Users/Zane/AppData/Local/Temp/RtmpSCWF6a/model-305c763066bb.hpp:396: note: by 'ulam_cmdstanr_4fe7673b04feaf50c3cdcaf9c5088fde_model_namespace::ulam_cmdstanr_4fe7673b04feaf50c3cdcaf9c5088fde_model::write_array'
396 | write_array(RNG& base_rng, std::vector<double>& params_r, std::vector<int>&
Running MCMC with 4 parallel chains, with 1 thread(s) per chain...
Chain 1 Iteration: 1 / 1000 [ 0%] (Warmup)
Chain 1 Iteration: 100 / 1000 [ 10%] (Warmup)
Chain 1 Iteration: 200 / 1000 [ 20%] (Warmup)
Chain 1 Iteration: 300 / 1000 [ 30%] (Warmup)
Chain 1 Iteration: 400 / 1000 [ 40%] (Warmup)
Chain 1 Iteration: 500 / 1000 [ 50%] (Warmup)
Chain 1 Iteration: 501 / 1000 [ 50%] (Sampling)
Chain 1 Iteration: 600 / 1000 [ 60%] (Sampling)
Chain 1 Iteration: 700 / 1000 [ 70%] (Sampling)
Chain 1 Iteration: 800 / 1000 [ 80%] (Sampling)
Chain 1 Iteration: 900 / 1000 [ 90%] (Sampling)
Chain 1 Iteration: 1000 / 1000 [100%] (Sampling)
Chain 2 Iteration: 1 / 1000 [ 0%] (Warmup)
Chain 2 Iteration: 100 / 1000 [ 10%] (Warmup)
Chain 2 Iteration: 200 / 1000 [ 20%] (Warmup)
Chain 2 Iteration: 300 / 1000 [ 30%] (Warmup)
Chain 2 Iteration: 400 / 1000 [ 40%] (Warmup)
Chain 2 Iteration: 500 / 1000 [ 50%] (Warmup)
Chain 2 Iteration: 501 / 1000 [ 50%] (Sampling)
Chain 2 Iteration: 600 / 1000 [ 60%] (Sampling)
Chain 2 Iteration: 700 / 1000 [ 70%] (Sampling)
Chain 2 Iteration: 800 / 1000 [ 80%] (Sampling)
Chain 2 Iteration: 900 / 1000 [ 90%] (Sampling)
Chain 2 Iteration: 1000 / 1000 [100%] (Sampling)
Chain 3 Iteration: 1 / 1000 [ 0%] (Warmup)
Chain 3 Iteration: 100 / 1000 [ 10%] (Warmup)
Chain 3 Iteration: 200 / 1000 [ 20%] (Warmup)
Chain 3 Iteration: 300 / 1000 [ 30%] (Warmup)
Chain 3 Iteration: 400 / 1000 [ 40%] (Warmup)
Chain 3 Iteration: 500 / 1000 [ 50%] (Warmup)
Chain 3 Iteration: 501 / 1000 [ 50%] (Sampling)
Chain 3 Iteration: 600 / 1000 [ 60%] (Sampling)
Chain 3 Iteration: 700 / 1000 [ 70%] (Sampling)
Chain 3 Iteration: 800 / 1000 [ 80%] (Sampling)
Chain 3 Iteration: 900 / 1000 [ 90%] (Sampling)
Chain 3 Iteration: 1000 / 1000 [100%] (Sampling)
Chain 4 Iteration: 1 / 1000 [ 0%] (Warmup)
Chain 4 Iteration: 100 / 1000 [ 10%] (Warmup)
Chain 4 Iteration: 200 / 1000 [ 20%] (Warmup)
Chain 4 Iteration: 300 / 1000 [ 30%] (Warmup)
Chain 4 Iteration: 400 / 1000 [ 40%] (Warmup)
Chain 4 Iteration: 500 / 1000 [ 50%] (Warmup)
Chain 4 Iteration: 501 / 1000 [ 50%] (Sampling)
Chain 4 Iteration: 600 / 1000 [ 60%] (Sampling)
Chain 4 Iteration: 700 / 1000 [ 70%] (Sampling)
Chain 4 Iteration: 800 / 1000 [ 80%] (Sampling)
Chain 4 Iteration: 900 / 1000 [ 90%] (Sampling)
Chain 4 Iteration: 1000 / 1000 [100%] (Sampling)
Chain 1 finished in 0.1 seconds.
Chain 2 finished in 0.1 seconds.
Chain 3 finished in 0.1 seconds.
Chain 4 finished in 0.1 seconds.
All 4 chains finished successfully.
Mean chain execution time: 0.1 seconds.
Total execution time: 0.3 seconds.
:: precis (m_11h4_4, depth = 3 )
mean sd 5.5% 94.5% rhat ess_bulk
a[1,1] -0.5345836 0.1696217 -0.8106720 -0.26461051 1.0008806 2294.621
a[2,1] -0.8716873 0.1534832 -1.1261138 -0.63142308 1.0006984 2727.746
a[3,1] -0.4768730 0.1775133 -0.7553812 -0.19071870 1.0038583 2986.386
a[4,1] -1.2241456 0.1330325 -1.4356773 -1.01263405 1.0006203 3038.263
a[5,1] -1.0949519 0.1454573 -1.3294144 -0.85795015 1.0045658 3287.659
a[6,1] -1.0122552 0.1690247 -1.2783505 -0.74334591 0.9997762 4185.266
a[7,1] -0.7571882 0.1462128 -0.9992067 -0.52254008 1.0110505 2943.007
a[8,1] -1.3649768 0.1057647 -1.5412999 -1.19883735 1.0017711 3331.298
a[9,1] -1.0652522 0.1278115 -1.2742692 -0.86215183 1.0013813 3433.822
a[1,2] -0.3624692 0.1967444 -0.6734129 -0.04018116 1.0025796 3210.047
a[2,2] -0.4139384 0.2033714 -0.7468464 -0.09520770 1.0017730 3397.567
a[3,2] -0.1376170 0.2317972 -0.4985326 0.22672325 1.0016368 3268.868
a[4,2] -0.9329249 0.1493878 -1.1644228 -0.69672024 0.9996920 3085.180
a[5,2] -0.5813657 0.1827433 -0.8741221 -0.28587571 1.0013636 2898.289
a[6,2] -0.6328828 0.1721165 -0.9025458 -0.36429156 0.9998270 2491.919
a[7,2] -0.9989299 0.1571183 -1.2482506 -0.74781338 1.0005676 3089.276
a[8,2] -1.5540676 0.1138381 -1.7390102 -1.37033195 1.0036889 2617.767
a[9,2] -1.4027613 0.1334975 -1.6172765 -1.19642820 1.0024347 2485.635
This model requires using the little ulam matrix trick, but it sampled really well and while we still have some very high uncertainties, they seem to be better overall from what I can glean from this table.
<- rethinking:: link (m_11h4_4)<- |> :: select (- awards) |> :: pivot_wider (names_from = gender, values_from = applications) |> :: summarize (p = f / (m + f), .by = discipline) |> :: arrange (- p) |> :: pull (discipline) |> as.character ()<- cbind (t (post) |> ` colnames<- ` (1 : nrow (post))|> :: select (- awards, - applications) |> :: pivot_longer (- c (gender, discipline), names_to = "draw" , values_to = "sample" |> :: summarize (:: mean_qi (sample, .width = 0.89 ),.by = c (gender, discipline)|> :: mutate (discipline = factor (discipline, levels = p_women_order)plot (x = 1 : 9 - k,y = subset (tidy_post, gender == "m" )$ y,xlab = "Discipline" ,xaxt = "n" ,ylab = "Chance of award acceptance" ,ylim = c (0 , 0.6 ),xlim = c (1 - k, 9 + k),col = "dodgerblue" arrows (x0 = 1 : 9 - k,x = 1 : 9 - k,y0 = subset (tidy_post, gender == "m" )$ ymin,y = subset (tidy_post, gender == "m" )$ ymax,length = 0.05 ,angle = 90 ,code = 3 ,col = "dodgerblue" points (x = 1 : 9 + k,y = subset (tidy_post, gender == "f" )$ y,col = "darkorange" arrows (x0 = 1 : 9 + k,x = 1 : 9 + k,y0 = subset (tidy_post, gender == "f" )$ ymin,y = subset (tidy_post, gender == "f" )$ ymax,length = 0.05 ,angle = 90 ,code = 3 ,col = "darkorange" axis (1 , at = 1 : 9 , labels = substr (p_women_order, 1 , 12 ))legend ("topright" ,lty = 1 , pch = 1 , col = c ("dodgerblue" , "darkorange" ),legend = c ("Men" , "Women" )
Now we can see what we actually expect from looking at the raw data, so it appears that correctly coding the interaction term makes a big difference. Now there are some disciplines where women appear to be more likely to get awards, while men are less likely to get awards. I ordered the categories by women being most likely to apply (women constituted the highest proportion of medical sciences applications and the lowest proportion of physics applications). So while it doesn’t seem like there is a systematic bias against women in the overall award process, I wonder if this reflects structural biases against women in certain disciplines, especially since physics and math are generally considered to be more male-dominated.
After I finished this, I reread the question and realized I was supposed to draw the dag so here it is.
<- dagitty:: dagitty ("dag { A <- G -> D -> A }" :: coordinates (p11h4_dag) <- list (x = c (G = 1 , D = 2 , A = 3 ),y = c (G = 2 , D = 1 , A = 2 )plot (p11h4_dag)
11H5
We’ll call the unobserved confound for the NWOGrants example \(U\) and we’ll first add it to our DAG. This confounder influences the mediator \(D\) and the outcome \(A\) .
<- dagitty:: dagitty ("dag { A <- G -> D -> A A <- U -> D }" :: coordinates (p11h5_dag) <- list (x = c (G = 1 , D = 2 , A = 2 , U = 1 ),y = c (G = 2 , D = 1 , A = 2 , U = 1 )plot (p11h5_dag)
Now when we condition on discipline, we open a backdoor path from \(G \to U \to A\) , which means that our causal effect estimate will be biased. We must condition on \(U\) to obtain an unbiased causal estimate, but we haven’t observed \(U\) so obtaining the unbiased estimate is impossible under this DAG. I didn’t need to simulate data because the answer here follows from the backdoor criterion rules discussed in chapters 5 and 6.
11H6
In this problem we’ll do some analysis of the primate data. We want to analyze the variables social_learning, research_effort, and brain, and since we haven’t dealt with missing data in this course yet, we’ll only deal with complete cases in those three variables. I’ll call them, respectively, \(L\) , \(R\) , and \(B\) .
data ("Primates301" , package = "rethinking" )<- |> :: transmute (name = as.character (name),L = social_learning,R = research_effort,R_l = log (R),B = brain,B_l = log (brain)|> :: drop_na () |> as.list ()# Can't pass names to stan but we might want to keep track of them <- P$ name$ name <- NULL
First we’ll model the number of observations of \(S\) , social learning, for each species, as a function for the log brain size, \(B\) . Let’s also fit a model with just an intercept to compare, since I think that’s usually a good idea.
<- rethinking:: ulam (alist (~ dpois (lambda),log (lambda) <- a,~ dnorm (3 , 0.5 )data = P,chains = 4 , cores = 4 ,log_lik = TRUE
In file included from stan/src/stan/model/model_header.hpp:5:
stan/src/stan/model/model_base_crtp.hpp:205:8: warning: 'void stan::model::model_base_crtp<M>::write_array(stan::rng_t&, std::vector<double>&, std::vector<int>&, std::vector<double>&, bool, bool, std::ostream*) const [with M = ulam_cmdstanr_bfee24f7aa8f2d4a6a716bf07ce5413e_model_namespace::ulam_cmdstanr_bfee24f7aa8f2d4a6a716bf07ce5413e_model; stan::rng_t = boost::random::mixmax_engine<17, 36, 0>; std::ostream = std::basic_ostream<char>]' was hidden [-Woverloaded-virtual=]
205 | void write_array(stan::rng_t& rng, std::vector<double>& theta,
| ^~~~~~~~~~~
C:/Users/Zane/AppData/Local/Temp/RtmpSCWF6a/model-305c3f7e34d1.hpp:421: note: by 'ulam_cmdstanr_bfee24f7aa8f2d4a6a716bf07ce5413e_model_namespace::ulam_cmdstanr_bfee24f7aa8f2d4a6a716bf07ce5413e_model::write_array'
421 | write_array(RNG& base_rng, std::vector<double>& params_r, std::vector<int>&
stan/src/stan/model/model_base_crtp.hpp:136:8: warning: 'void stan::model::model_base_crtp<M>::write_array(stan::rng_t&, Eigen::VectorXd&, Eigen::VectorXd&, bool, bool, std::ostream*) const [with M = ulam_cmdstanr_bfee24f7aa8f2d4a6a716bf07ce5413e_model_namespace::ulam_cmdstanr_bfee24f7aa8f2d4a6a716bf07ce5413e_model; stan::rng_t = boost::random::mixmax_engine<17, 36, 0>; Eigen::VectorXd = Eigen::Matrix<double, -1, 1>; std::ostream = std::basic_ostream<char>]' was hidden [-Woverloaded-virtual=]
136 | void write_array(stan::rng_t& rng, Eigen::VectorXd& theta,
| ^~~~~~~~~~~
C:/Users/Zane/AppData/Local/Temp/RtmpSCWF6a/model-305c3f7e34d1.hpp:421: note: by 'ulam_cmdstanr_bfee24f7aa8f2d4a6a716bf07ce5413e_model_namespace::ulam_cmdstanr_bfee24f7aa8f2d4a6a716bf07ce5413e_model::write_array'
421 | write_array(RNG& base_rng, std::vector<double>& params_r, std::vector<int>&
Running MCMC with 4 parallel chains, with 1 thread(s) per chain...
Chain 1 Iteration: 1 / 1000 [ 0%] (Warmup)
Chain 1 Iteration: 100 / 1000 [ 10%] (Warmup)
Chain 1 Iteration: 200 / 1000 [ 20%] (Warmup)
Chain 1 Iteration: 300 / 1000 [ 30%] (Warmup)
Chain 1 Iteration: 400 / 1000 [ 40%] (Warmup)
Chain 1 Iteration: 500 / 1000 [ 50%] (Warmup)
Chain 1 Iteration: 501 / 1000 [ 50%] (Sampling)
Chain 1 Iteration: 600 / 1000 [ 60%] (Sampling)
Chain 1 Iteration: 700 / 1000 [ 70%] (Sampling)
Chain 1 Iteration: 800 / 1000 [ 80%] (Sampling)
Chain 1 Iteration: 900 / 1000 [ 90%] (Sampling)
Chain 2 Iteration: 1 / 1000 [ 0%] (Warmup)
Chain 2 Iteration: 100 / 1000 [ 10%] (Warmup)
Chain 2 Iteration: 200 / 1000 [ 20%] (Warmup)
Chain 2 Iteration: 300 / 1000 [ 30%] (Warmup)
Chain 2 Iteration: 400 / 1000 [ 40%] (Warmup)
Chain 2 Iteration: 500 / 1000 [ 50%] (Warmup)
Chain 2 Iteration: 501 / 1000 [ 50%] (Sampling)
Chain 2 Iteration: 600 / 1000 [ 60%] (Sampling)
Chain 2 Iteration: 700 / 1000 [ 70%] (Sampling)
Chain 2 Iteration: 800 / 1000 [ 80%] (Sampling)
Chain 2 Iteration: 900 / 1000 [ 90%] (Sampling)
Chain 2 Iteration: 1000 / 1000 [100%] (Sampling)
Chain 3 Iteration: 1 / 1000 [ 0%] (Warmup)
Chain 3 Iteration: 100 / 1000 [ 10%] (Warmup)
Chain 3 Iteration: 200 / 1000 [ 20%] (Warmup)
Chain 3 Iteration: 300 / 1000 [ 30%] (Warmup)
Chain 3 Iteration: 400 / 1000 [ 40%] (Warmup)
Chain 3 Iteration: 500 / 1000 [ 50%] (Warmup)
Chain 3 Iteration: 501 / 1000 [ 50%] (Sampling)
Chain 3 Iteration: 600 / 1000 [ 60%] (Sampling)
Chain 3 Iteration: 700 / 1000 [ 70%] (Sampling)
Chain 3 Iteration: 800 / 1000 [ 80%] (Sampling)
Chain 4 Iteration: 1 / 1000 [ 0%] (Warmup)
Chain 4 Iteration: 100 / 1000 [ 10%] (Warmup)
Chain 4 Iteration: 200 / 1000 [ 20%] (Warmup)
Chain 4 Iteration: 300 / 1000 [ 30%] (Warmup)
Chain 4 Iteration: 400 / 1000 [ 40%] (Warmup)
Chain 4 Iteration: 500 / 1000 [ 50%] (Warmup)
Chain 4 Iteration: 501 / 1000 [ 50%] (Sampling)
Chain 4 Iteration: 600 / 1000 [ 60%] (Sampling)
Chain 1 Iteration: 1000 / 1000 [100%] (Sampling)
Chain 1 finished in 0.1 seconds.
Chain 2 finished in 0.1 seconds.
Chain 3 Iteration: 900 / 1000 [ 90%] (Sampling)
Chain 3 Iteration: 1000 / 1000 [100%] (Sampling)
Chain 3 finished in 0.1 seconds.
Chain 4 Iteration: 700 / 1000 [ 70%] (Sampling)
Chain 4 Iteration: 800 / 1000 [ 80%] (Sampling)
Chain 4 Iteration: 900 / 1000 [ 90%] (Sampling)
Chain 4 Iteration: 1000 / 1000 [100%] (Sampling)
Chain 4 finished in 0.1 seconds.
All 4 chains finished successfully.
Mean chain execution time: 0.1 seconds.
Total execution time: 0.3 seconds.
:: precis (m_11h6_1)
mean sd 5.5% 94.5% rhat ess_bulk
a 1.147359 0.04742073 1.069905 1.222499 1.008879 683.8726
The model didn’t sample fantastically but it sampled OK, the rhat is fine even though we have lower ESS than samples by a decent amount. But hopefully adding the predictor of interest will help.
<- rethinking:: ulam (alist (~ dpois (lambda),log (lambda) <- a + bB * B_l,~ dnorm (3 , 0.5 ),~ dnorm (0 , 0.2 )data = P,chains = 4 , cores = 4 ,iter = 2500 , warmup = 500 ,log_lik = TRUE
In file included from stan/src/stan/model/model_header.hpp:5:
stan/src/stan/model/model_base_crtp.hpp:205:8: warning: 'void stan::model::model_base_crtp<M>::write_array(stan::rng_t&, std::vector<double>&, std::vector<int>&, std::vector<double>&, bool, bool, std::ostream*) const [with M = ulam_cmdstanr_b7a2e4397427bc172d753660d7248461_model_namespace::ulam_cmdstanr_b7a2e4397427bc172d753660d7248461_model; stan::rng_t = boost::random::mixmax_engine<17, 36, 0>; std::ostream = std::basic_ostream<char>]' was hidden [-Woverloaded-virtual=]
205 | void write_array(stan::rng_t& rng, std::vector<double>& theta,
| ^~~~~~~~~~~
C:/Users/Zane/AppData/Local/Temp/RtmpSCWF6a/model-305c109d6183.hpp:491: note: by 'ulam_cmdstanr_b7a2e4397427bc172d753660d7248461_model_namespace::ulam_cmdstanr_b7a2e4397427bc172d753660d7248461_model::write_array'
491 | write_array(RNG& base_rng, std::vector<double>& params_r, std::vector<int>&
stan/src/stan/model/model_base_crtp.hpp:136:8: warning: 'void stan::model::model_base_crtp<M>::write_array(stan::rng_t&, Eigen::VectorXd&, Eigen::VectorXd&, bool, bool, std::ostream*) const [with M = ulam_cmdstanr_b7a2e4397427bc172d753660d7248461_model_namespace::ulam_cmdstanr_b7a2e4397427bc172d753660d7248461_model; stan::rng_t = boost::random::mixmax_engine<17, 36, 0>; Eigen::VectorXd = Eigen::Matrix<double, -1, 1>; std::ostream = std::basic_ostream<char>]' was hidden [-Woverloaded-virtual=]
136 | void write_array(stan::rng_t& rng, Eigen::VectorXd& theta,
| ^~~~~~~~~~~
C:/Users/Zane/AppData/Local/Temp/RtmpSCWF6a/model-305c109d6183.hpp:491: note: by 'ulam_cmdstanr_b7a2e4397427bc172d753660d7248461_model_namespace::ulam_cmdstanr_b7a2e4397427bc172d753660d7248461_model::write_array'
491 | write_array(RNG& base_rng, std::vector<double>& params_r, std::vector<int>&
Running MCMC with 4 parallel chains, with 1 thread(s) per chain...
Chain 1 Iteration: 1 / 2500 [ 0%] (Warmup)
Chain 1 Iteration: 100 / 2500 [ 4%] (Warmup)
Chain 1 Iteration: 200 / 2500 [ 8%] (Warmup)
Chain 2 Iteration: 1 / 2500 [ 0%] (Warmup)
Chain 2 Iteration: 100 / 2500 [ 4%] (Warmup)
Chain 2 Iteration: 200 / 2500 [ 8%] (Warmup)
Chain 3 Iteration: 1 / 2500 [ 0%] (Warmup)
Chain 3 Iteration: 100 / 2500 [ 4%] (Warmup)
Chain 3 Iteration: 200 / 2500 [ 8%] (Warmup)
Chain 4 Iteration: 1 / 2500 [ 0%] (Warmup)
Chain 4 Iteration: 100 / 2500 [ 4%] (Warmup)
Chain 4 Iteration: 200 / 2500 [ 8%] (Warmup)
Chain 1 Iteration: 300 / 2500 [ 12%] (Warmup)
Chain 1 Iteration: 400 / 2500 [ 16%] (Warmup)
Chain 1 Iteration: 500 / 2500 [ 20%] (Warmup)
Chain 1 Iteration: 501 / 2500 [ 20%] (Sampling)
Chain 1 Iteration: 600 / 2500 [ 24%] (Sampling)
Chain 1 Iteration: 700 / 2500 [ 28%] (Sampling)
Chain 2 Iteration: 300 / 2500 [ 12%] (Warmup)
Chain 2 Iteration: 400 / 2500 [ 16%] (Warmup)
Chain 2 Iteration: 500 / 2500 [ 20%] (Warmup)
Chain 2 Iteration: 501 / 2500 [ 20%] (Sampling)
Chain 2 Iteration: 600 / 2500 [ 24%] (Sampling)
Chain 2 Iteration: 700 / 2500 [ 28%] (Sampling)
Chain 2 Iteration: 800 / 2500 [ 32%] (Sampling)
Chain 3 Iteration: 300 / 2500 [ 12%] (Warmup)
Chain 3 Iteration: 400 / 2500 [ 16%] (Warmup)
Chain 3 Iteration: 500 / 2500 [ 20%] (Warmup)
Chain 3 Iteration: 501 / 2500 [ 20%] (Sampling)
Chain 3 Iteration: 600 / 2500 [ 24%] (Sampling)
Chain 3 Iteration: 700 / 2500 [ 28%] (Sampling)
Chain 4 Iteration: 300 / 2500 [ 12%] (Warmup)
Chain 4 Iteration: 400 / 2500 [ 16%] (Warmup)
Chain 4 Iteration: 500 / 2500 [ 20%] (Warmup)
Chain 4 Iteration: 501 / 2500 [ 20%] (Sampling)
Chain 4 Iteration: 600 / 2500 [ 24%] (Sampling)
Chain 4 Iteration: 700 / 2500 [ 28%] (Sampling)
Chain 1 Iteration: 800 / 2500 [ 32%] (Sampling)
Chain 1 Iteration: 900 / 2500 [ 36%] (Sampling)
Chain 2 Iteration: 900 / 2500 [ 36%] (Sampling)
Chain 2 Iteration: 1000 / 2500 [ 40%] (Sampling)
Chain 3 Iteration: 800 / 2500 [ 32%] (Sampling)
Chain 3 Iteration: 900 / 2500 [ 36%] (Sampling)
Chain 3 Iteration: 1000 / 2500 [ 40%] (Sampling)
Chain 4 Iteration: 800 / 2500 [ 32%] (Sampling)
Chain 4 Iteration: 900 / 2500 [ 36%] (Sampling)
Chain 4 Iteration: 1000 / 2500 [ 40%] (Sampling)
Chain 1 Iteration: 1000 / 2500 [ 40%] (Sampling)
Chain 1 Iteration: 1100 / 2500 [ 44%] (Sampling)
Chain 1 Iteration: 1200 / 2500 [ 48%] (Sampling)
Chain 2 Iteration: 1100 / 2500 [ 44%] (Sampling)
Chain 2 Iteration: 1200 / 2500 [ 48%] (Sampling)
Chain 2 Iteration: 1300 / 2500 [ 52%] (Sampling)
Chain 3 Iteration: 1100 / 2500 [ 44%] (Sampling)
Chain 3 Iteration: 1200 / 2500 [ 48%] (Sampling)
Chain 4 Iteration: 1100 / 2500 [ 44%] (Sampling)
Chain 4 Iteration: 1200 / 2500 [ 48%] (Sampling)
Chain 1 Iteration: 1300 / 2500 [ 52%] (Sampling)
Chain 1 Iteration: 1400 / 2500 [ 56%] (Sampling)
Chain 2 Iteration: 1400 / 2500 [ 56%] (Sampling)
Chain 2 Iteration: 1500 / 2500 [ 60%] (Sampling)
Chain 3 Iteration: 1300 / 2500 [ 52%] (Sampling)
Chain 3 Iteration: 1400 / 2500 [ 56%] (Sampling)
Chain 3 Iteration: 1500 / 2500 [ 60%] (Sampling)
Chain 4 Iteration: 1300 / 2500 [ 52%] (Sampling)
Chain 4 Iteration: 1400 / 2500 [ 56%] (Sampling)
Chain 4 Iteration: 1500 / 2500 [ 60%] (Sampling)
Chain 1 Iteration: 1500 / 2500 [ 60%] (Sampling)
Chain 1 Iteration: 1600 / 2500 [ 64%] (Sampling)
Chain 2 Iteration: 1600 / 2500 [ 64%] (Sampling)
Chain 2 Iteration: 1700 / 2500 [ 68%] (Sampling)
Chain 2 Iteration: 1800 / 2500 [ 72%] (Sampling)
Chain 3 Iteration: 1600 / 2500 [ 64%] (Sampling)
Chain 3 Iteration: 1700 / 2500 [ 68%] (Sampling)
Chain 4 Iteration: 1600 / 2500 [ 64%] (Sampling)
Chain 4 Iteration: 1700 / 2500 [ 68%] (Sampling)
Chain 1 Iteration: 1700 / 2500 [ 68%] (Sampling)
Chain 1 Iteration: 1800 / 2500 [ 72%] (Sampling)
Chain 1 Iteration: 1900 / 2500 [ 76%] (Sampling)
Chain 2 Iteration: 1900 / 2500 [ 76%] (Sampling)
Chain 2 Iteration: 2000 / 2500 [ 80%] (Sampling)
Chain 3 Iteration: 1800 / 2500 [ 72%] (Sampling)
Chain 3 Iteration: 1900 / 2500 [ 76%] (Sampling)
Chain 4 Iteration: 1800 / 2500 [ 72%] (Sampling)
Chain 4 Iteration: 1900 / 2500 [ 76%] (Sampling)
Chain 1 Iteration: 2000 / 2500 [ 80%] (Sampling)
Chain 1 Iteration: 2100 / 2500 [ 84%] (Sampling)
Chain 2 Iteration: 2100 / 2500 [ 84%] (Sampling)
Chain 2 Iteration: 2200 / 2500 [ 88%] (Sampling)
Chain 3 Iteration: 2000 / 2500 [ 80%] (Sampling)
Chain 3 Iteration: 2100 / 2500 [ 84%] (Sampling)
Chain 3 Iteration: 2200 / 2500 [ 88%] (Sampling)
Chain 4 Iteration: 2000 / 2500 [ 80%] (Sampling)
Chain 4 Iteration: 2100 / 2500 [ 84%] (Sampling)
Chain 4 Iteration: 2200 / 2500 [ 88%] (Sampling)
Chain 1 Iteration: 2200 / 2500 [ 88%] (Sampling)
Chain 1 Iteration: 2300 / 2500 [ 92%] (Sampling)
Chain 2 Iteration: 2300 / 2500 [ 92%] (Sampling)
Chain 2 Iteration: 2400 / 2500 [ 96%] (Sampling)
Chain 2 Iteration: 2500 / 2500 [100%] (Sampling)
Chain 3 Iteration: 2300 / 2500 [ 92%] (Sampling)
Chain 4 Iteration: 2300 / 2500 [ 92%] (Sampling)
Chain 4 Iteration: 2400 / 2500 [ 96%] (Sampling)
Chain 2 finished in 1.1 seconds.
Chain 1 Iteration: 2400 / 2500 [ 96%] (Sampling)
Chain 1 Iteration: 2500 / 2500 [100%] (Sampling)
Chain 3 Iteration: 2400 / 2500 [ 96%] (Sampling)
Chain 3 Iteration: 2500 / 2500 [100%] (Sampling)
Chain 4 Iteration: 2500 / 2500 [100%] (Sampling)
Chain 1 finished in 1.2 seconds.
Chain 3 finished in 1.2 seconds.
Chain 4 finished in 1.1 seconds.
All 4 chains finished successfully.
Mean chain execution time: 1.2 seconds.
Total execution time: 1.3 seconds.
:: precis (m_11h6_2)
mean sd 5.5% 94.5% rhat ess_bulk
a -5.702611 0.23895294 -6.084772 -5.318667 1.001962 1266.447
bB 1.566239 0.04771101 1.489867 1.642044 1.001871 1270.222
Adding the predictor didn’t seem to help the sampling, I had to run some more samples than the default to get rhat values of 1. But that’s not so bad. We get a fairly tight posterior CI for the parameter bB, the effect of log brain size on the rate of mentions of social learning in literature. We can quickly make sure this is better than the intercept only model, even though it seems obvious that it is.
:: compare (m_11h6_1, m_11h6_2, sort = "PSIS" , func = PSIS)
Some Pareto k values are very high (>1). Set pointwise=TRUE to inspect individual points.
Some Pareto k values are very high (>1). Set pointwise=TRUE to inspect individual points.
PSIS SE dPSIS dSE pPSIS weight
m_11h6_2 1495.885 520.9707 0.000 NA 99.09490 1.00000e+00
m_11h6_1 2945.699 1499.4572 1449.814 1006.558 68.07411 1.50296e-315
There are some influential points in the data, which makes sense cause there’s a lot of 0’s in the \(L\) variable and not too many primates with the highest brain sizes. But our model with the brain size predictor in it is MUCH better than the intercept-only model, which is great. I think we should take a quick look at these different variables though. I’ll log \(R\) and \(B\) before plotting them, but we can’t take the log of \(L\) because it has zeroes in it.
data.frame (L = P$ L, "log R" = log (P$ R), "log B" = log (P$ B)) |> :: ggpairs () + :: theme_minimal (base_size = 18 )
Registered S3 method overwritten by 'GGally':
method from
+.gg ggplot2
Yeah, it is no surprise that there are influential points once we see the distribution of \(L\) , we can tell which ones are influential. It seems that the primates with the most social learning mentions also have high \(R\) and \(B\) values.
Anyways, we should finish interpreting the model we fit with the log brain size. Let’s go ahead and plot the predictions.
<- seq (1 , 600 , 10 )<- log (B_seq)<- rethinking:: link (m_11h6_2, data = data.frame (B_l = B_seq_log))<- apply (post, 2 , mean)<- apply (post, 2 , rethinking:: PI)plot ($ B_l, P$ L,xlab = "Brain mass (cc^3)" ,ylab = "Social learning mentions" ,xaxt = "n" lines (lwd = 2 :: shade (<- c (1 , 2.5 , 5 , 10 , 25 , 50 , 100 , 250 , 500 )axis (1 , at = log (axis_vals), axis_vals)
The credible interval for the predictions are quite tight, and the predictions are dominated by the primates with zero or very few social learning mentions, which are predicted quite well by the model. We slightly overpredict the number of social learning mentions for primates with around 100 - 250 cc3 brain mass, and slightly underpredict some outliers. The primates with the highest brain mass values are hard to predict and we do a bad job there.
Since some primates are studied much more often, we also want to account for this in our model, using the variable \(R\) (and particularly \(\log R\) ), since this should account for part of the mentions of social learning in the literature. Let’s go ahead and fit a model that just has these two independent predictors.
<- rethinking:: ulam (alist (~ dpois (lambda),log (lambda) <- a + bB * B_l + bR * R_l,~ dnorm (3 , 0.5 ),~ dnorm (0 , 0.2 ),~ dnorm (0 , 0.2 )data = P,chains = 4 , cores = 4 ,iter = 2500 , warmup = 500 ,log_lik = TRUE
In file included from stan/src/stan/model/model_header.hpp:5:
stan/src/stan/model/model_base_crtp.hpp:205:8: warning: 'void stan::model::model_base_crtp<M>::write_array(stan::rng_t&, std::vector<double>&, std::vector<int>&, std::vector<double>&, bool, bool, std::ostream*) const [with M = ulam_cmdstanr_26a9e7f4fe82ce851c4df53d960c70d0_model_namespace::ulam_cmdstanr_26a9e7f4fe82ce851c4df53d960c70d0_model; stan::rng_t = boost::random::mixmax_engine<17, 36, 0>; std::ostream = std::basic_ostream<char>]' was hidden [-Woverloaded-virtual=]
205 | void write_array(stan::rng_t& rng, std::vector<double>& theta,
| ^~~~~~~~~~~
C:/Users/Zane/AppData/Local/Temp/RtmpSCWF6a/model-305c23247a80.hpp:523: note: by 'ulam_cmdstanr_26a9e7f4fe82ce851c4df53d960c70d0_model_namespace::ulam_cmdstanr_26a9e7f4fe82ce851c4df53d960c70d0_model::write_array'
523 | write_array(RNG& base_rng, std::vector<double>& params_r, std::vector<int>&
stan/src/stan/model/model_base_crtp.hpp:136:8: warning: 'void stan::model::model_base_crtp<M>::write_array(stan::rng_t&, Eigen::VectorXd&, Eigen::VectorXd&, bool, bool, std::ostream*) const [with M = ulam_cmdstanr_26a9e7f4fe82ce851c4df53d960c70d0_model_namespace::ulam_cmdstanr_26a9e7f4fe82ce851c4df53d960c70d0_model; stan::rng_t = boost::random::mixmax_engine<17, 36, 0>; Eigen::VectorXd = Eigen::Matrix<double, -1, 1>; std::ostream = std::basic_ostream<char>]' was hidden [-Woverloaded-virtual=]
136 | void write_array(stan::rng_t& rng, Eigen::VectorXd& theta,
| ^~~~~~~~~~~
C:/Users/Zane/AppData/Local/Temp/RtmpSCWF6a/model-305c23247a80.hpp:523: note: by 'ulam_cmdstanr_26a9e7f4fe82ce851c4df53d960c70d0_model_namespace::ulam_cmdstanr_26a9e7f4fe82ce851c4df53d960c70d0_model::write_array'
523 | write_array(RNG& base_rng, std::vector<double>& params_r, std::vector<int>&
Running MCMC with 4 parallel chains, with 1 thread(s) per chain...
Chain 1 Iteration: 1 / 2500 [ 0%] (Warmup)
Chain 1 Iteration: 100 / 2500 [ 4%] (Warmup)
Chain 2 Iteration: 1 / 2500 [ 0%] (Warmup)
Chain 2 Iteration: 100 / 2500 [ 4%] (Warmup)
Chain 3 Iteration: 1 / 2500 [ 0%] (Warmup)
Chain 3 Iteration: 100 / 2500 [ 4%] (Warmup)
Chain 4 Iteration: 1 / 2500 [ 0%] (Warmup)
Chain 4 Iteration: 100 / 2500 [ 4%] (Warmup)
Chain 1 Iteration: 200 / 2500 [ 8%] (Warmup)
Chain 1 Iteration: 300 / 2500 [ 12%] (Warmup)
Chain 1 Iteration: 400 / 2500 [ 16%] (Warmup)
Chain 1 Iteration: 500 / 2500 [ 20%] (Warmup)
Chain 1 Iteration: 501 / 2500 [ 20%] (Sampling)
Chain 2 Iteration: 200 / 2500 [ 8%] (Warmup)
Chain 2 Iteration: 300 / 2500 [ 12%] (Warmup)
Chain 2 Iteration: 400 / 2500 [ 16%] (Warmup)
Chain 3 Iteration: 200 / 2500 [ 8%] (Warmup)
Chain 3 Iteration: 300 / 2500 [ 12%] (Warmup)
Chain 4 Iteration: 200 / 2500 [ 8%] (Warmup)
Chain 4 Iteration: 300 / 2500 [ 12%] (Warmup)
Chain 1 Iteration: 600 / 2500 [ 24%] (Sampling)
Chain 2 Iteration: 500 / 2500 [ 20%] (Warmup)
Chain 2 Iteration: 501 / 2500 [ 20%] (Sampling)
Chain 2 Iteration: 600 / 2500 [ 24%] (Sampling)
Chain 3 Iteration: 400 / 2500 [ 16%] (Warmup)
Chain 3 Iteration: 500 / 2500 [ 20%] (Warmup)
Chain 3 Iteration: 501 / 2500 [ 20%] (Sampling)
Chain 4 Iteration: 400 / 2500 [ 16%] (Warmup)
Chain 4 Iteration: 500 / 2500 [ 20%] (Warmup)
Chain 4 Iteration: 501 / 2500 [ 20%] (Sampling)
Chain 1 Iteration: 700 / 2500 [ 28%] (Sampling)
Chain 1 Iteration: 800 / 2500 [ 32%] (Sampling)
Chain 2 Iteration: 700 / 2500 [ 28%] (Sampling)
Chain 3 Iteration: 600 / 2500 [ 24%] (Sampling)
Chain 4 Iteration: 600 / 2500 [ 24%] (Sampling)
Chain 1 Iteration: 900 / 2500 [ 36%] (Sampling)
Chain 2 Iteration: 800 / 2500 [ 32%] (Sampling)
Chain 2 Iteration: 900 / 2500 [ 36%] (Sampling)
Chain 3 Iteration: 700 / 2500 [ 28%] (Sampling)
Chain 3 Iteration: 800 / 2500 [ 32%] (Sampling)
Chain 4 Iteration: 700 / 2500 [ 28%] (Sampling)
Chain 4 Iteration: 800 / 2500 [ 32%] (Sampling)
Chain 1 Iteration: 1000 / 2500 [ 40%] (Sampling)
Chain 2 Iteration: 1000 / 2500 [ 40%] (Sampling)
Chain 3 Iteration: 900 / 2500 [ 36%] (Sampling)
Chain 4 Iteration: 900 / 2500 [ 36%] (Sampling)
Chain 1 Iteration: 1100 / 2500 [ 44%] (Sampling)
Chain 1 Iteration: 1200 / 2500 [ 48%] (Sampling)
Chain 2 Iteration: 1100 / 2500 [ 44%] (Sampling)
Chain 3 Iteration: 1000 / 2500 [ 40%] (Sampling)
Chain 4 Iteration: 1000 / 2500 [ 40%] (Sampling)
Chain 1 Iteration: 1300 / 2500 [ 52%] (Sampling)
Chain 2 Iteration: 1200 / 2500 [ 48%] (Sampling)
Chain 2 Iteration: 1300 / 2500 [ 52%] (Sampling)
Chain 3 Iteration: 1100 / 2500 [ 44%] (Sampling)
Chain 3 Iteration: 1200 / 2500 [ 48%] (Sampling)
Chain 4 Iteration: 1100 / 2500 [ 44%] (Sampling)
Chain 4 Iteration: 1200 / 2500 [ 48%] (Sampling)
Chain 1 Iteration: 1400 / 2500 [ 56%] (Sampling)
Chain 2 Iteration: 1400 / 2500 [ 56%] (Sampling)
Chain 3 Iteration: 1300 / 2500 [ 52%] (Sampling)
Chain 3 Iteration: 1400 / 2500 [ 56%] (Sampling)
Chain 4 Iteration: 1300 / 2500 [ 52%] (Sampling)
Chain 1 Iteration: 1500 / 2500 [ 60%] (Sampling)
Chain 1 Iteration: 1600 / 2500 [ 64%] (Sampling)
Chain 2 Iteration: 1500 / 2500 [ 60%] (Sampling)
Chain 2 Iteration: 1600 / 2500 [ 64%] (Sampling)
Chain 3 Iteration: 1500 / 2500 [ 60%] (Sampling)
Chain 4 Iteration: 1400 / 2500 [ 56%] (Sampling)
Chain 1 Iteration: 1700 / 2500 [ 68%] (Sampling)
Chain 2 Iteration: 1700 / 2500 [ 68%] (Sampling)
Chain 3 Iteration: 1600 / 2500 [ 64%] (Sampling)
Chain 3 Iteration: 1700 / 2500 [ 68%] (Sampling)
Chain 4 Iteration: 1500 / 2500 [ 60%] (Sampling)
Chain 4 Iteration: 1600 / 2500 [ 64%] (Sampling)
Chain 1 Iteration: 1800 / 2500 [ 72%] (Sampling)
Chain 2 Iteration: 1800 / 2500 [ 72%] (Sampling)
Chain 2 Iteration: 1900 / 2500 [ 76%] (Sampling)
Chain 3 Iteration: 1800 / 2500 [ 72%] (Sampling)
Chain 4 Iteration: 1700 / 2500 [ 68%] (Sampling)
Chain 1 Iteration: 1900 / 2500 [ 76%] (Sampling)
Chain 1 Iteration: 2000 / 2500 [ 80%] (Sampling)
Chain 2 Iteration: 2000 / 2500 [ 80%] (Sampling)
Chain 3 Iteration: 1900 / 2500 [ 76%] (Sampling)
Chain 3 Iteration: 2000 / 2500 [ 80%] (Sampling)
Chain 4 Iteration: 1800 / 2500 [ 72%] (Sampling)
Chain 1 Iteration: 2100 / 2500 [ 84%] (Sampling)
Chain 2 Iteration: 2100 / 2500 [ 84%] (Sampling)
Chain 2 Iteration: 2200 / 2500 [ 88%] (Sampling)
Chain 3 Iteration: 2100 / 2500 [ 84%] (Sampling)
Chain 4 Iteration: 1900 / 2500 [ 76%] (Sampling)
Chain 4 Iteration: 2000 / 2500 [ 80%] (Sampling)
Chain 1 Iteration: 2200 / 2500 [ 88%] (Sampling)
Chain 2 Iteration: 2300 / 2500 [ 92%] (Sampling)
Chain 3 Iteration: 2200 / 2500 [ 88%] (Sampling)
Chain 3 Iteration: 2300 / 2500 [ 92%] (Sampling)
Chain 4 Iteration: 2100 / 2500 [ 84%] (Sampling)
Chain 1 Iteration: 2300 / 2500 [ 92%] (Sampling)
Chain 1 Iteration: 2400 / 2500 [ 96%] (Sampling)
Chain 2 Iteration: 2400 / 2500 [ 96%] (Sampling)
Chain 3 Iteration: 2400 / 2500 [ 96%] (Sampling)
Chain 4 Iteration: 2200 / 2500 [ 88%] (Sampling)
Chain 2 Iteration: 2500 / 2500 [100%] (Sampling)
Chain 2 finished in 1.9 seconds.
Chain 1 Iteration: 2500 / 2500 [100%] (Sampling)
Chain 3 Iteration: 2500 / 2500 [100%] (Sampling)
Chain 4 Iteration: 2300 / 2500 [ 92%] (Sampling)
Chain 4 Iteration: 2400 / 2500 [ 96%] (Sampling)
Chain 1 finished in 2.0 seconds.
Chain 3 finished in 1.9 seconds.
Chain 4 Iteration: 2500 / 2500 [100%] (Sampling)
Chain 4 finished in 2.1 seconds.
All 4 chains finished successfully.
Mean chain execution time: 2.0 seconds.
Total execution time: 2.2 seconds.
:: precis (m_11h6_3)
mean sd 5.5% 94.5% rhat ess_bulk
a -5.2808024 0.20397485 -5.6090022 -4.9559251 1.001776 3448.115
bB 0.2354209 0.05101455 0.1554321 0.3183224 1.002106 2692.249
bR 1.3085272 0.04988509 1.2280389 1.3883138 1.001088 2706.957
First let’s compare this model to the previous model without the effect of \(R\) , although judging by the coefficient estimates, both predictors are important.
:: coeftab (m_11h6_2, m_11h6_3) |> :: coeftab_plot ()
We can see that the effect of \(B\) is much reduced in model 3, which also contains the effect of \(R\) , which itself has a strong positive effect. That indicates that once we know how much research effort has been put into studying a primate, knowing its brain size doesn’t influence the number of social learning mentions quite as much, but it’s still important.
Now we’ll draw a DAG for this problem. We know that \(B\) and \(R\) both affect \(S\) , but the question of interest is whether there is any relationship between \(B\) and \(R\) . I think that species with higher brain sizes are probably studied more, because we expect to see more social learning activities in those species – they’re more interesting to scientists because they display more complex behaviors. So that would mean that we have a path \(B \to R\) in addition to the paths \(B \to S\) and \(R \to S\) , and \(R\) mediates the effect of \(B\) on \(S\) . Let’s draw that dag.
<- dagitty:: dagitty ("dag { B -> S R -> S B -> R }" :: coordinates (p11h6_dag) <- list (x = c (B = 1 , R = 1.5 , S = 2 ),y = c (B = 2 , R = 1 , S = 2 )plot (p11h6_dag)
Our analysis also supports this DAG (of course there are many other DAGs that would be supported by the same results). We saw an effect of \(B\) on \(S\) , but then in a model with both \(B\) and \(R\) , we saw that \(R\) had an effect on \(S\) , and \(B\) still had an effect on \(S\) but a less strong effect. I think one more justification for this model would be to fit a model with \(R\) and \(S\) only, and the model with both covariates should be better than any of the other models.
<- rethinking:: ulam (alist (~ dpois (lambda),log (lambda) <- a + bR * R_l,~ dnorm (3 , 0.5 ),~ dnorm (0 , 0.2 )data = P,chains = 4 , cores = 4 ,iter = 2500 , warmup = 500 ,log_lik = TRUE
In file included from stan/src/stan/model/model_header.hpp:5:
stan/src/stan/model/model_base_crtp.hpp:205:8: warning: 'void stan::model::model_base_crtp<M>::write_array(stan::rng_t&, std::vector<double>&, std::vector<int>&, std::vector<double>&, bool, bool, std::ostream*) const [with M = ulam_cmdstanr_acec846f4d370e6515a350313c664088_model_namespace::ulam_cmdstanr_acec846f4d370e6515a350313c664088_model; stan::rng_t = boost::random::mixmax_engine<17, 36, 0>; std::ostream = std::basic_ostream<char>]' was hidden [-Woverloaded-virtual=]
205 | void write_array(stan::rng_t& rng, std::vector<double>& theta,
| ^~~~~~~~~~~
C:/Users/Zane/AppData/Local/Temp/RtmpSCWF6a/model-305c15fb6bd2.hpp:491: note: by 'ulam_cmdstanr_acec846f4d370e6515a350313c664088_model_namespace::ulam_cmdstanr_acec846f4d370e6515a350313c664088_model::write_array'
491 | write_array(RNG& base_rng, std::vector<double>& params_r, std::vector<int>&
stan/src/stan/model/model_base_crtp.hpp:136:8: warning: 'void stan::model::model_base_crtp<M>::write_array(stan::rng_t&, Eigen::VectorXd&, Eigen::VectorXd&, bool, bool, std::ostream*) const [with M = ulam_cmdstanr_acec846f4d370e6515a350313c664088_model_namespace::ulam_cmdstanr_acec846f4d370e6515a350313c664088_model; stan::rng_t = boost::random::mixmax_engine<17, 36, 0>; Eigen::VectorXd = Eigen::Matrix<double, -1, 1>; std::ostream = std::basic_ostream<char>]' was hidden [-Woverloaded-virtual=]
136 | void write_array(stan::rng_t& rng, Eigen::VectorXd& theta,
| ^~~~~~~~~~~
C:/Users/Zane/AppData/Local/Temp/RtmpSCWF6a/model-305c15fb6bd2.hpp:491: note: by 'ulam_cmdstanr_acec846f4d370e6515a350313c664088_model_namespace::ulam_cmdstanr_acec846f4d370e6515a350313c664088_model::write_array'
491 | write_array(RNG& base_rng, std::vector<double>& params_r, std::vector<int>&
Running MCMC with 4 parallel chains, with 1 thread(s) per chain...
Chain 1 Iteration: 1 / 2500 [ 0%] (Warmup)
Chain 1 Iteration: 100 / 2500 [ 4%] (Warmup)
Chain 1 Iteration: 200 / 2500 [ 8%] (Warmup)
Chain 2 Iteration: 1 / 2500 [ 0%] (Warmup)
Chain 2 Iteration: 100 / 2500 [ 4%] (Warmup)
Chain 2 Iteration: 200 / 2500 [ 8%] (Warmup)
Chain 3 Iteration: 1 / 2500 [ 0%] (Warmup)
Chain 3 Iteration: 100 / 2500 [ 4%] (Warmup)
Chain 4 Iteration: 1 / 2500 [ 0%] (Warmup)
Chain 4 Iteration: 100 / 2500 [ 4%] (Warmup)
Chain 1 Iteration: 300 / 2500 [ 12%] (Warmup)
Chain 1 Iteration: 400 / 2500 [ 16%] (Warmup)
Chain 1 Iteration: 500 / 2500 [ 20%] (Warmup)
Chain 1 Iteration: 501 / 2500 [ 20%] (Sampling)
Chain 1 Iteration: 600 / 2500 [ 24%] (Sampling)
Chain 1 Iteration: 700 / 2500 [ 28%] (Sampling)
Chain 1 Iteration: 800 / 2500 [ 32%] (Sampling)
Chain 2 Iteration: 300 / 2500 [ 12%] (Warmup)
Chain 2 Iteration: 400 / 2500 [ 16%] (Warmup)
Chain 2 Iteration: 500 / 2500 [ 20%] (Warmup)
Chain 2 Iteration: 501 / 2500 [ 20%] (Sampling)
Chain 2 Iteration: 600 / 2500 [ 24%] (Sampling)
Chain 2 Iteration: 700 / 2500 [ 28%] (Sampling)
Chain 3 Iteration: 200 / 2500 [ 8%] (Warmup)
Chain 3 Iteration: 300 / 2500 [ 12%] (Warmup)
Chain 3 Iteration: 400 / 2500 [ 16%] (Warmup)
Chain 3 Iteration: 500 / 2500 [ 20%] (Warmup)
Chain 3 Iteration: 501 / 2500 [ 20%] (Sampling)
Chain 3 Iteration: 600 / 2500 [ 24%] (Sampling)
Chain 3 Iteration: 700 / 2500 [ 28%] (Sampling)
Chain 4 Iteration: 200 / 2500 [ 8%] (Warmup)
Chain 4 Iteration: 300 / 2500 [ 12%] (Warmup)
Chain 4 Iteration: 400 / 2500 [ 16%] (Warmup)
Chain 4 Iteration: 500 / 2500 [ 20%] (Warmup)
Chain 4 Iteration: 501 / 2500 [ 20%] (Sampling)
Chain 4 Iteration: 600 / 2500 [ 24%] (Sampling)
Chain 4 Iteration: 700 / 2500 [ 28%] (Sampling)
Chain 1 Iteration: 900 / 2500 [ 36%] (Sampling)
Chain 1 Iteration: 1000 / 2500 [ 40%] (Sampling)
Chain 2 Iteration: 800 / 2500 [ 32%] (Sampling)
Chain 2 Iteration: 900 / 2500 [ 36%] (Sampling)
Chain 3 Iteration: 800 / 2500 [ 32%] (Sampling)
Chain 3 Iteration: 900 / 2500 [ 36%] (Sampling)
Chain 3 Iteration: 1000 / 2500 [ 40%] (Sampling)
Chain 4 Iteration: 800 / 2500 [ 32%] (Sampling)
Chain 4 Iteration: 900 / 2500 [ 36%] (Sampling)
Chain 1 Iteration: 1100 / 2500 [ 44%] (Sampling)
Chain 1 Iteration: 1200 / 2500 [ 48%] (Sampling)
Chain 1 Iteration: 1300 / 2500 [ 52%] (Sampling)
Chain 2 Iteration: 1000 / 2500 [ 40%] (Sampling)
Chain 2 Iteration: 1100 / 2500 [ 44%] (Sampling)
Chain 2 Iteration: 1200 / 2500 [ 48%] (Sampling)
Chain 3 Iteration: 1100 / 2500 [ 44%] (Sampling)
Chain 3 Iteration: 1200 / 2500 [ 48%] (Sampling)
Chain 4 Iteration: 1000 / 2500 [ 40%] (Sampling)
Chain 4 Iteration: 1100 / 2500 [ 44%] (Sampling)
Chain 4 Iteration: 1200 / 2500 [ 48%] (Sampling)
Chain 1 Iteration: 1400 / 2500 [ 56%] (Sampling)
Chain 1 Iteration: 1500 / 2500 [ 60%] (Sampling)
Chain 2 Iteration: 1300 / 2500 [ 52%] (Sampling)
Chain 2 Iteration: 1400 / 2500 [ 56%] (Sampling)
Chain 3 Iteration: 1300 / 2500 [ 52%] (Sampling)
Chain 3 Iteration: 1400 / 2500 [ 56%] (Sampling)
Chain 3 Iteration: 1500 / 2500 [ 60%] (Sampling)
Chain 4 Iteration: 1300 / 2500 [ 52%] (Sampling)
Chain 4 Iteration: 1400 / 2500 [ 56%] (Sampling)
Chain 1 Iteration: 1600 / 2500 [ 64%] (Sampling)
Chain 1 Iteration: 1700 / 2500 [ 68%] (Sampling)
Chain 1 Iteration: 1800 / 2500 [ 72%] (Sampling)
Chain 2 Iteration: 1500 / 2500 [ 60%] (Sampling)
Chain 2 Iteration: 1600 / 2500 [ 64%] (Sampling)
Chain 2 Iteration: 1700 / 2500 [ 68%] (Sampling)
Chain 3 Iteration: 1600 / 2500 [ 64%] (Sampling)
Chain 3 Iteration: 1700 / 2500 [ 68%] (Sampling)
Chain 4 Iteration: 1500 / 2500 [ 60%] (Sampling)
Chain 4 Iteration: 1600 / 2500 [ 64%] (Sampling)
Chain 4 Iteration: 1700 / 2500 [ 68%] (Sampling)
Chain 1 Iteration: 1900 / 2500 [ 76%] (Sampling)
Chain 1 Iteration: 2000 / 2500 [ 80%] (Sampling)
Chain 2 Iteration: 1800 / 2500 [ 72%] (Sampling)
Chain 2 Iteration: 1900 / 2500 [ 76%] (Sampling)
Chain 3 Iteration: 1800 / 2500 [ 72%] (Sampling)
Chain 3 Iteration: 1900 / 2500 [ 76%] (Sampling)
Chain 3 Iteration: 2000 / 2500 [ 80%] (Sampling)
Chain 4 Iteration: 1800 / 2500 [ 72%] (Sampling)
Chain 4 Iteration: 1900 / 2500 [ 76%] (Sampling)
Chain 1 Iteration: 2100 / 2500 [ 84%] (Sampling)
Chain 1 Iteration: 2200 / 2500 [ 88%] (Sampling)
Chain 1 Iteration: 2300 / 2500 [ 92%] (Sampling)
Chain 2 Iteration: 2000 / 2500 [ 80%] (Sampling)
Chain 2 Iteration: 2100 / 2500 [ 84%] (Sampling)
Chain 3 Iteration: 2100 / 2500 [ 84%] (Sampling)
Chain 3 Iteration: 2200 / 2500 [ 88%] (Sampling)
Chain 4 Iteration: 2000 / 2500 [ 80%] (Sampling)
Chain 4 Iteration: 2100 / 2500 [ 84%] (Sampling)
Chain 4 Iteration: 2200 / 2500 [ 88%] (Sampling)
Chain 1 Iteration: 2400 / 2500 [ 96%] (Sampling)
Chain 1 Iteration: 2500 / 2500 [100%] (Sampling)
Chain 2 Iteration: 2200 / 2500 [ 88%] (Sampling)
Chain 2 Iteration: 2300 / 2500 [ 92%] (Sampling)
Chain 3 Iteration: 2300 / 2500 [ 92%] (Sampling)
Chain 3 Iteration: 2400 / 2500 [ 96%] (Sampling)
Chain 4 Iteration: 2300 / 2500 [ 92%] (Sampling)
Chain 4 Iteration: 2400 / 2500 [ 96%] (Sampling)
Chain 1 finished in 1.2 seconds.
Chain 2 Iteration: 2400 / 2500 [ 96%] (Sampling)
Chain 2 Iteration: 2500 / 2500 [100%] (Sampling)
Chain 2 finished in 1.2 seconds.
Chain 3 Iteration: 2500 / 2500 [100%] (Sampling)
Chain 3 finished in 1.2 seconds.
Chain 4 Iteration: 2500 / 2500 [100%] (Sampling)
Chain 4 finished in 1.2 seconds.
All 4 chains finished successfully.
Mean chain execution time: 1.2 seconds.
Total execution time: 1.4 seconds.
:: precis (m_11h6_4)
mean sd 5.5% 94.5% rhat ess_bulk
a -5.059805 0.2059833 -5.390855 -4.730125 1.002896 1302.561
bR 1.483728 0.0373488 1.423330 1.543341 1.002294 1280.760
We can see that there’s still a strong effect of \(R\) , but let’s compare the coefficents from the other two models.
:: coeftab (m_11h6_2, m_11h6_3, m_11h6_4) |> :: coeftab_plot ()
Yes, we can see that the effect of \(R\) is slightly stronger in this model than it is in the model with both \(B\) and \(R\) . This suggests that part of the effect of \(R\) in the \(R\) -only model is actually the causal effect of \(B\) passing through \(R\) . So this also makes sense if mediation is the true causal story here. Finally, let’s do a quick PSIS comparison.
:: compare (sort = "PSIS" , func = PSIS
Some Pareto k values are very high (>1). Set pointwise=TRUE to inspect individual points.
Some Pareto k values are very high (>1). Set pointwise=TRUE to inspect individual points.
Some Pareto k values are very high (>1). Set pointwise=TRUE to inspect individual points.
PSIS SE dPSIS dSE pPSIS weight
m_11h6_3 649.0007 161.8579 0.00000 NA 58.75646 9.995776e-01
m_11h6_4 664.5390 156.2038 15.53833 34.79137 50.07368 4.223880e-04
m_11h6_2 1495.8848 520.9707 846.88407 410.15501 99.09490 1.262631e-184
From our PSIS model, it seems that \(R\) is much more important than \(B\) for predicting \(S\) , which makes sense to me since \(S\) is the number of literature mentions. The model with both covariates is slightly better, but not in any appreciable sense given the standard errors. Finally, I think it makes sense to fit a model to test whether the mediation effect is really necessary – we can built a two stage model where \(B\) acts on \(R\) , and \(R\) alone acts on \(S\) .
<- rethinking:: ulam (alist (~ dpois (lambda),log (lambda) <- a + bR * R_l,~ dpois (gamma),log (gamma) <- q + zB * B_l,~ dnorm (3 , 0.5 ),~ dnorm (3 , 0.5 ),~ dnorm (0 , 0.2 ),~ dnorm (0 , 0.2 )data = P,chains = 4 , cores = 4 ,iter = 2500 , warmup = 500 ,log_lik = TRUE
In file included from stan/src/stan/model/model_header.hpp:5:
stan/src/stan/model/model_base_crtp.hpp:205:8: warning: 'void stan::model::model_base_crtp<M>::write_array(stan::rng_t&, std::vector<double>&, std::vector<int>&, std::vector<double>&, bool, bool, std::ostream*) const [with M = ulam_cmdstanr_bff832798202135d67c9c33051e169db_model_namespace::ulam_cmdstanr_bff832798202135d67c9c33051e169db_model; stan::rng_t = boost::random::mixmax_engine<17, 36, 0>; std::ostream = std::basic_ostream<char>]' was hidden [-Woverloaded-virtual=]
205 | void write_array(stan::rng_t& rng, std::vector<double>& theta,
| ^~~~~~~~~~~
C:/Users/Zane/AppData/Local/Temp/RtmpSCWF6a/model-305c6b942434.hpp:602: note: by 'ulam_cmdstanr_bff832798202135d67c9c33051e169db_model_namespace::ulam_cmdstanr_bff832798202135d67c9c33051e169db_model::write_array'
602 | write_array(RNG& base_rng, std::vector<double>& params_r, std::vector<int>&
stan/src/stan/model/model_base_crtp.hpp:136:8: warning: 'void stan::model::model_base_crtp<M>::write_array(stan::rng_t&, Eigen::VectorXd&, Eigen::VectorXd&, bool, bool, std::ostream*) const [with M = ulam_cmdstanr_bff832798202135d67c9c33051e169db_model_namespace::ulam_cmdstanr_bff832798202135d67c9c33051e169db_model; stan::rng_t = boost::random::mixmax_engine<17, 36, 0>; Eigen::VectorXd = Eigen::Matrix<double, -1, 1>; std::ostream = std::basic_ostream<char>]' was hidden [-Woverloaded-virtual=]
136 | void write_array(stan::rng_t& rng, Eigen::VectorXd& theta,
| ^~~~~~~~~~~
C:/Users/Zane/AppData/Local/Temp/RtmpSCWF6a/model-305c6b942434.hpp:602: note: by 'ulam_cmdstanr_bff832798202135d67c9c33051e169db_model_namespace::ulam_cmdstanr_bff832798202135d67c9c33051e169db_model::write_array'
602 | write_array(RNG& base_rng, std::vector<double>& params_r, std::vector<int>&
Running MCMC with 4 parallel chains, with 1 thread(s) per chain...
Chain 1 Iteration: 1 / 2500 [ 0%] (Warmup)
Chain 1 Iteration: 100 / 2500 [ 4%] (Warmup)
Chain 2 Iteration: 1 / 2500 [ 0%] (Warmup)
Chain 3 Iteration: 1 / 2500 [ 0%] (Warmup)
Chain 4 Iteration: 1 / 2500 [ 0%] (Warmup)
Chain 1 Iteration: 200 / 2500 [ 8%] (Warmup)
Chain 1 Iteration: 300 / 2500 [ 12%] (Warmup)
Chain 2 Iteration: 100 / 2500 [ 4%] (Warmup)
Chain 2 Iteration: 200 / 2500 [ 8%] (Warmup)
Chain 2 Iteration: 300 / 2500 [ 12%] (Warmup)
Chain 3 Iteration: 100 / 2500 [ 4%] (Warmup)
Chain 3 Iteration: 200 / 2500 [ 8%] (Warmup)
Chain 4 Iteration: 100 / 2500 [ 4%] (Warmup)
Chain 4 Iteration: 200 / 2500 [ 8%] (Warmup)
Chain 4 Iteration: 300 / 2500 [ 12%] (Warmup)
Chain 1 Iteration: 400 / 2500 [ 16%] (Warmup)
Chain 2 Iteration: 400 / 2500 [ 16%] (Warmup)
Chain 3 Iteration: 300 / 2500 [ 12%] (Warmup)
Chain 3 Iteration: 400 / 2500 [ 16%] (Warmup)
Chain 4 Iteration: 400 / 2500 [ 16%] (Warmup)
Chain 1 Iteration: 500 / 2500 [ 20%] (Warmup)
Chain 1 Iteration: 501 / 2500 [ 20%] (Sampling)
Chain 2 Iteration: 500 / 2500 [ 20%] (Warmup)
Chain 2 Iteration: 501 / 2500 [ 20%] (Sampling)
Chain 3 Iteration: 500 / 2500 [ 20%] (Warmup)
Chain 3 Iteration: 501 / 2500 [ 20%] (Sampling)
Chain 4 Iteration: 500 / 2500 [ 20%] (Warmup)
Chain 4 Iteration: 501 / 2500 [ 20%] (Sampling)
Chain 1 Iteration: 600 / 2500 [ 24%] (Sampling)
Chain 1 Iteration: 700 / 2500 [ 28%] (Sampling)
Chain 2 Iteration: 600 / 2500 [ 24%] (Sampling)
Chain 2 Iteration: 700 / 2500 [ 28%] (Sampling)
Chain 3 Iteration: 600 / 2500 [ 24%] (Sampling)
Chain 4 Iteration: 600 / 2500 [ 24%] (Sampling)
Chain 1 Iteration: 800 / 2500 [ 32%] (Sampling)
Chain 2 Iteration: 800 / 2500 [ 32%] (Sampling)
Chain 3 Iteration: 700 / 2500 [ 28%] (Sampling)
Chain 4 Iteration: 700 / 2500 [ 28%] (Sampling)
Chain 4 Iteration: 800 / 2500 [ 32%] (Sampling)
Chain 1 Iteration: 900 / 2500 [ 36%] (Sampling)
Chain 2 Iteration: 900 / 2500 [ 36%] (Sampling)
Chain 3 Iteration: 800 / 2500 [ 32%] (Sampling)
Chain 4 Iteration: 900 / 2500 [ 36%] (Sampling)
Chain 1 Iteration: 1000 / 2500 [ 40%] (Sampling)
Chain 2 Iteration: 1000 / 2500 [ 40%] (Sampling)
Chain 3 Iteration: 900 / 2500 [ 36%] (Sampling)
Chain 4 Iteration: 1000 / 2500 [ 40%] (Sampling)
Chain 1 Iteration: 1100 / 2500 [ 44%] (Sampling)
Chain 1 Iteration: 1200 / 2500 [ 48%] (Sampling)
Chain 2 Iteration: 1100 / 2500 [ 44%] (Sampling)
Chain 3 Iteration: 1000 / 2500 [ 40%] (Sampling)
Chain 3 Iteration: 1100 / 2500 [ 44%] (Sampling)
Chain 4 Iteration: 1100 / 2500 [ 44%] (Sampling)
Chain 4 Iteration: 1200 / 2500 [ 48%] (Sampling)
Chain 1 Iteration: 1300 / 2500 [ 52%] (Sampling)
Chain 2 Iteration: 1200 / 2500 [ 48%] (Sampling)
Chain 3 Iteration: 1200 / 2500 [ 48%] (Sampling)
Chain 4 Iteration: 1300 / 2500 [ 52%] (Sampling)
Chain 1 Iteration: 1400 / 2500 [ 56%] (Sampling)
Chain 2 Iteration: 1300 / 2500 [ 52%] (Sampling)
Chain 3 Iteration: 1300 / 2500 [ 52%] (Sampling)
Chain 4 Iteration: 1400 / 2500 [ 56%] (Sampling)
Chain 1 Iteration: 1500 / 2500 [ 60%] (Sampling)
Chain 2 Iteration: 1400 / 2500 [ 56%] (Sampling)
Chain 3 Iteration: 1400 / 2500 [ 56%] (Sampling)
Chain 4 Iteration: 1500 / 2500 [ 60%] (Sampling)
Chain 1 Iteration: 1600 / 2500 [ 64%] (Sampling)
Chain 1 Iteration: 1700 / 2500 [ 68%] (Sampling)
Chain 2 Iteration: 1500 / 2500 [ 60%] (Sampling)
Chain 3 Iteration: 1500 / 2500 [ 60%] (Sampling)
Chain 4 Iteration: 1600 / 2500 [ 64%] (Sampling)
Chain 4 Iteration: 1700 / 2500 [ 68%] (Sampling)
Chain 1 Iteration: 1800 / 2500 [ 72%] (Sampling)
Chain 2 Iteration: 1600 / 2500 [ 64%] (Sampling)
Chain 3 Iteration: 1600 / 2500 [ 64%] (Sampling)
Chain 4 Iteration: 1800 / 2500 [ 72%] (Sampling)
Chain 1 Iteration: 1900 / 2500 [ 76%] (Sampling)
Chain 2 Iteration: 1700 / 2500 [ 68%] (Sampling)
Chain 3 Iteration: 1700 / 2500 [ 68%] (Sampling)
Chain 3 Iteration: 1800 / 2500 [ 72%] (Sampling)
Chain 4 Iteration: 1900 / 2500 [ 76%] (Sampling)
Chain 1 Iteration: 2000 / 2500 [ 80%] (Sampling)
Chain 2 Iteration: 1800 / 2500 [ 72%] (Sampling)
Chain 3 Iteration: 1900 / 2500 [ 76%] (Sampling)
Chain 4 Iteration: 2000 / 2500 [ 80%] (Sampling)
Chain 1 Iteration: 2100 / 2500 [ 84%] (Sampling)
Chain 2 Iteration: 1900 / 2500 [ 76%] (Sampling)
Chain 3 Iteration: 2000 / 2500 [ 80%] (Sampling)
Chain 4 Iteration: 2100 / 2500 [ 84%] (Sampling)
Chain 1 Iteration: 2200 / 2500 [ 88%] (Sampling)
Chain 2 Iteration: 2000 / 2500 [ 80%] (Sampling)
Chain 3 Iteration: 2100 / 2500 [ 84%] (Sampling)
Chain 4 Iteration: 2200 / 2500 [ 88%] (Sampling)
Chain 1 Iteration: 2300 / 2500 [ 92%] (Sampling)
Chain 1 Iteration: 2400 / 2500 [ 96%] (Sampling)
Chain 2 Iteration: 2100 / 2500 [ 84%] (Sampling)
Chain 3 Iteration: 2200 / 2500 [ 88%] (Sampling)
Chain 4 Iteration: 2300 / 2500 [ 92%] (Sampling)
Chain 4 Iteration: 2400 / 2500 [ 96%] (Sampling)
Chain 1 Iteration: 2500 / 2500 [100%] (Sampling)
Chain 2 Iteration: 2200 / 2500 [ 88%] (Sampling)
Chain 3 Iteration: 2300 / 2500 [ 92%] (Sampling)
Chain 4 Iteration: 2500 / 2500 [100%] (Sampling)
Chain 1 finished in 2.4 seconds.
Chain 4 finished in 2.3 seconds.
Chain 2 Iteration: 2300 / 2500 [ 92%] (Sampling)
Chain 2 Iteration: 2400 / 2500 [ 96%] (Sampling)
Chain 3 Iteration: 2400 / 2500 [ 96%] (Sampling)
Chain 3 Iteration: 2500 / 2500 [100%] (Sampling)
Chain 3 finished in 2.5 seconds.
Chain 2 Iteration: 2500 / 2500 [100%] (Sampling)
Chain 2 finished in 2.6 seconds.
All 4 chains finished successfully.
Mean chain execution time: 2.4 seconds.
Total execution time: 2.7 seconds.
:: precis (m_11h6_5)
mean sd 5.5% 94.5% rhat ess_bulk
a -4.18160920 0.18826935 -4.4814665 -3.8859423 1.002185 2429.975
q 0.63752986 0.15617473 0.3853957 0.8820185 1.000505 2853.881
bR 1.44179177 0.03763236 1.3822789 1.5009999 1.002234 2485.043
zB 0.07387559 0.03996772 0.0104592 0.1383845 1.000695 2791.187
I was somewhat worried that this model would not be identifiable since Poisson distributions can collapse together, but it seems to actually have sampled pretty well. Here we can see that there’s a weak effect of \(B\) on \(R\) , but a stronger effect of \(R\) on \(S\) , and we’re fairly confident in both of these effects. So to some extent, brain size does contribute to research effort, but it can’t be the only factor in chosing which species are studied. If we look back at our plot, there is a general trend between log \(R\) and log \(B\) , but a lot of spread, so this result seems to make sense. Let’s see if we can fit a model that has effects of \(B\) in both places.
<- rethinking:: ulam (alist (~ dpois (lambda),log (lambda) <- a + bR * R_l + bB * B_l,~ dpois (gamma),log (gamma) <- q + zB * B_l,~ dnorm (3 , 0.5 ),~ dnorm (3 , 0.5 ),~ dnorm (0 , 0.2 ),~ dnorm (0 , 0.2 ),~ dnorm (0 , 0.2 )data = P,chains = 4 , cores = 4 ,iter = 2500 , warmup = 500 ,log_lik = TRUE
In file included from stan/src/stan/model/model_header.hpp:5:
stan/src/stan/model/model_base_crtp.hpp:205:8: warning: 'void stan::model::model_base_crtp<M>::write_array(stan::rng_t&, std::vector<double>&, std::vector<int>&, std::vector<double>&, bool, bool, std::ostream*) const [with M = ulam_cmdstanr_de46c453c17beac95b8495d7624e7713_model_namespace::ulam_cmdstanr_de46c453c17beac95b8495d7624e7713_model; stan::rng_t = boost::random::mixmax_engine<17, 36, 0>; std::ostream = std::basic_ostream<char>]' was hidden [-Woverloaded-virtual=]
205 | void write_array(stan::rng_t& rng, std::vector<double>& theta,
| ^~~~~~~~~~~
C:/Users/Zane/AppData/Local/Temp/RtmpSCWF6a/model-305c26274117.hpp:634: note: by 'ulam_cmdstanr_de46c453c17beac95b8495d7624e7713_model_namespace::ulam_cmdstanr_de46c453c17beac95b8495d7624e7713_model::write_array'
634 | write_array(RNG& base_rng, std::vector<double>& params_r, std::vector<int>&
stan/src/stan/model/model_base_crtp.hpp:136:8: warning: 'void stan::model::model_base_crtp<M>::write_array(stan::rng_t&, Eigen::VectorXd&, Eigen::VectorXd&, bool, bool, std::ostream*) const [with M = ulam_cmdstanr_de46c453c17beac95b8495d7624e7713_model_namespace::ulam_cmdstanr_de46c453c17beac95b8495d7624e7713_model; stan::rng_t = boost::random::mixmax_engine<17, 36, 0>; Eigen::VectorXd = Eigen::Matrix<double, -1, 1>; std::ostream = std::basic_ostream<char>]' was hidden [-Woverloaded-virtual=]
136 | void write_array(stan::rng_t& rng, Eigen::VectorXd& theta,
| ^~~~~~~~~~~
C:/Users/Zane/AppData/Local/Temp/RtmpSCWF6a/model-305c26274117.hpp:634: note: by 'ulam_cmdstanr_de46c453c17beac95b8495d7624e7713_model_namespace::ulam_cmdstanr_de46c453c17beac95b8495d7624e7713_model::write_array'
634 | write_array(RNG& base_rng, std::vector<double>& params_r, std::vector<int>&
Running MCMC with 4 parallel chains, with 1 thread(s) per chain...
Chain 1 Iteration: 1 / 2500 [ 0%] (Warmup)
Chain 2 Iteration: 1 / 2500 [ 0%] (Warmup)
Chain 3 Iteration: 1 / 2500 [ 0%] (Warmup)
Chain 4 Iteration: 1 / 2500 [ 0%] (Warmup)
Chain 1 Iteration: 100 / 2500 [ 4%] (Warmup)
Chain 1 Iteration: 200 / 2500 [ 8%] (Warmup)
Chain 2 Iteration: 100 / 2500 [ 4%] (Warmup)
Chain 2 Iteration: 200 / 2500 [ 8%] (Warmup)
Chain 3 Iteration: 100 / 2500 [ 4%] (Warmup)
Chain 4 Iteration: 100 / 2500 [ 4%] (Warmup)
Chain 1 Iteration: 300 / 2500 [ 12%] (Warmup)
Chain 3 Iteration: 200 / 2500 [ 8%] (Warmup)
Chain 4 Iteration: 200 / 2500 [ 8%] (Warmup)
Chain 1 Iteration: 400 / 2500 [ 16%] (Warmup)
Chain 2 Iteration: 300 / 2500 [ 12%] (Warmup)
Chain 3 Iteration: 300 / 2500 [ 12%] (Warmup)
Chain 4 Iteration: 300 / 2500 [ 12%] (Warmup)
Chain 1 Iteration: 500 / 2500 [ 20%] (Warmup)
Chain 1 Iteration: 501 / 2500 [ 20%] (Sampling)
Chain 2 Iteration: 400 / 2500 [ 16%] (Warmup)
Chain 3 Iteration: 400 / 2500 [ 16%] (Warmup)
Chain 4 Iteration: 400 / 2500 [ 16%] (Warmup)
Chain 2 Iteration: 500 / 2500 [ 20%] (Warmup)
Chain 2 Iteration: 501 / 2500 [ 20%] (Sampling)
Chain 3 Iteration: 500 / 2500 [ 20%] (Warmup)
Chain 3 Iteration: 501 / 2500 [ 20%] (Sampling)
Chain 1 Iteration: 600 / 2500 [ 24%] (Sampling)
Chain 2 Iteration: 600 / 2500 [ 24%] (Sampling)
Chain 4 Iteration: 500 / 2500 [ 20%] (Warmup)
Chain 1 Iteration: 700 / 2500 [ 28%] (Sampling)
Chain 3 Iteration: 600 / 2500 [ 24%] (Sampling)
Chain 4 Iteration: 501 / 2500 [ 20%] (Sampling)
Chain 4 Iteration: 600 / 2500 [ 24%] (Sampling)
Chain 1 Iteration: 800 / 2500 [ 32%] (Sampling)
Chain 2 Iteration: 700 / 2500 [ 28%] (Sampling)
Chain 3 Iteration: 700 / 2500 [ 28%] (Sampling)
Chain 4 Iteration: 700 / 2500 [ 28%] (Sampling)
Chain 2 Iteration: 800 / 2500 [ 32%] (Sampling)
Chain 3 Iteration: 800 / 2500 [ 32%] (Sampling)
Chain 4 Iteration: 800 / 2500 [ 32%] (Sampling)
Chain 1 Iteration: 900 / 2500 [ 36%] (Sampling)
Chain 2 Iteration: 900 / 2500 [ 36%] (Sampling)
Chain 1 Iteration: 1000 / 2500 [ 40%] (Sampling)
Chain 2 Iteration: 1000 / 2500 [ 40%] (Sampling)
Chain 3 Iteration: 900 / 2500 [ 36%] (Sampling)
Chain 4 Iteration: 900 / 2500 [ 36%] (Sampling)
Chain 3 Iteration: 1000 / 2500 [ 40%] (Sampling)
Chain 4 Iteration: 1000 / 2500 [ 40%] (Sampling)
Chain 1 Iteration: 1100 / 2500 [ 44%] (Sampling)
Chain 2 Iteration: 1100 / 2500 [ 44%] (Sampling)
Chain 1 Iteration: 1200 / 2500 [ 48%] (Sampling)
Chain 2 Iteration: 1200 / 2500 [ 48%] (Sampling)
Chain 3 Iteration: 1100 / 2500 [ 44%] (Sampling)
Chain 4 Iteration: 1100 / 2500 [ 44%] (Sampling)
Chain 1 Iteration: 1300 / 2500 [ 52%] (Sampling)
Chain 2 Iteration: 1300 / 2500 [ 52%] (Sampling)
Chain 3 Iteration: 1200 / 2500 [ 48%] (Sampling)
Chain 4 Iteration: 1200 / 2500 [ 48%] (Sampling)
Chain 3 Iteration: 1300 / 2500 [ 52%] (Sampling)
Chain 4 Iteration: 1300 / 2500 [ 52%] (Sampling)
Chain 1 Iteration: 1400 / 2500 [ 56%] (Sampling)
Chain 2 Iteration: 1400 / 2500 [ 56%] (Sampling)
Chain 1 Iteration: 1500 / 2500 [ 60%] (Sampling)
Chain 2 Iteration: 1500 / 2500 [ 60%] (Sampling)
Chain 3 Iteration: 1400 / 2500 [ 56%] (Sampling)
Chain 4 Iteration: 1400 / 2500 [ 56%] (Sampling)
Chain 1 Iteration: 1600 / 2500 [ 64%] (Sampling)
Chain 2 Iteration: 1600 / 2500 [ 64%] (Sampling)
Chain 3 Iteration: 1500 / 2500 [ 60%] (Sampling)
Chain 4 Iteration: 1500 / 2500 [ 60%] (Sampling)
Chain 2 Iteration: 1700 / 2500 [ 68%] (Sampling)
Chain 3 Iteration: 1600 / 2500 [ 64%] (Sampling)
Chain 4 Iteration: 1600 / 2500 [ 64%] (Sampling)
Chain 1 Iteration: 1700 / 2500 [ 68%] (Sampling)
Chain 1 Iteration: 1800 / 2500 [ 72%] (Sampling)
Chain 2 Iteration: 1800 / 2500 [ 72%] (Sampling)
Chain 3 Iteration: 1700 / 2500 [ 68%] (Sampling)
Chain 4 Iteration: 1700 / 2500 [ 68%] (Sampling)
Chain 1 Iteration: 1900 / 2500 [ 76%] (Sampling)
Chain 2 Iteration: 1900 / 2500 [ 76%] (Sampling)
Chain 3 Iteration: 1800 / 2500 [ 72%] (Sampling)
Chain 4 Iteration: 1800 / 2500 [ 72%] (Sampling)
Chain 2 Iteration: 2000 / 2500 [ 80%] (Sampling)
Chain 3 Iteration: 1900 / 2500 [ 76%] (Sampling)
Chain 4 Iteration: 1900 / 2500 [ 76%] (Sampling)
Chain 1 Iteration: 2000 / 2500 [ 80%] (Sampling)
Chain 2 Iteration: 2100 / 2500 [ 84%] (Sampling)
Chain 1 Iteration: 2100 / 2500 [ 84%] (Sampling)
Chain 3 Iteration: 2000 / 2500 [ 80%] (Sampling)
Chain 4 Iteration: 2000 / 2500 [ 80%] (Sampling)
Chain 1 Iteration: 2200 / 2500 [ 88%] (Sampling)
Chain 2 Iteration: 2200 / 2500 [ 88%] (Sampling)
Chain 3 Iteration: 2100 / 2500 [ 84%] (Sampling)
Chain 4 Iteration: 2100 / 2500 [ 84%] (Sampling)
Chain 2 Iteration: 2300 / 2500 [ 92%] (Sampling)
Chain 3 Iteration: 2200 / 2500 [ 88%] (Sampling)
Chain 4 Iteration: 2200 / 2500 [ 88%] (Sampling)
Chain 1 Iteration: 2300 / 2500 [ 92%] (Sampling)
Chain 2 Iteration: 2400 / 2500 [ 96%] (Sampling)
Chain 1 Iteration: 2400 / 2500 [ 96%] (Sampling)
Chain 3 Iteration: 2300 / 2500 [ 92%] (Sampling)
Chain 4 Iteration: 2300 / 2500 [ 92%] (Sampling)
Chain 1 Iteration: 2500 / 2500 [100%] (Sampling)
Chain 2 Iteration: 2500 / 2500 [100%] (Sampling)
Chain 3 Iteration: 2400 / 2500 [ 96%] (Sampling)
Chain 4 Iteration: 2400 / 2500 [ 96%] (Sampling)
Chain 1 finished in 3.7 seconds.
Chain 2 finished in 3.6 seconds.
Chain 3 Iteration: 2500 / 2500 [100%] (Sampling)
Chain 4 Iteration: 2500 / 2500 [100%] (Sampling)
Chain 3 finished in 3.8 seconds.
Chain 4 finished in 3.8 seconds.
All 4 chains finished successfully.
Mean chain execution time: 3.7 seconds.
Total execution time: 3.8 seconds.
:: precis (m_11h6_6)
mean sd 5.5% 94.5% rhat ess_bulk
a -4.69287655 0.19215605 -5.001124750 -4.3933962 1.000958 4289.015
q 0.63876960 0.15591546 0.385178150 0.8855043 1.001777 3448.827
bR 1.17913335 0.04719371 1.105567350 1.2546266 1.003634 4171.952
bB 0.36636054 0.04730110 0.291621725 0.4416572 1.001608 4062.840
zB 0.07363362 0.03997097 0.009998887 0.1373845 1.001248 3539.679
Yes, here we can actually seem to distinguish between the effect of \(B\) on \(R\) (the parameter zB, which is fairly small) and the effect of \(B\) on \(S\) (the parameter bB which is larger). That’s interesting and I think it does seem to support our mediation hypothesis.