library(rethinking)This chapter is about models where the data likelihood is a “mixture” distribution: the student \(t\) distribution is a replacement for Gaussian likelihoods with many outliers; beta-binomial and gamma-Poisson are replacements for binomial and Poisson likelihoods respectively that allow for more heterogeneity in the data; and zero-inflated or hurdle models allow for discrete point masses of probability that arise from different processes. While these models don’t give us causal information about what is happening in our data, they can help us get more robust inferences about other things we care about.
We also learned about models for categorical variables with a specific order, the cumulative logit model for outcomes and a monotonicty constraint with dirichlet priors for predictors.
Exercises
12E1
An ordered categorical variable has a natural order for the levels so it makes sense to put them in a specific order, while an unordered (nominal) categorical variable doesn’t have a natural ordering. Specifically, we can say that an ordered category variable has levels that increase or decrease in order, even if we can’t quantify the amount of change between each level.
An example of an ordered categorical variable is a symptom score, which is designed to be higher if a patient experiences more symptoms or more severe symptoms during an illness, but a change in symptom score from 1 to 2 may not be the same as from 5 to 6. An example of an unordered categorical variable is ABO blood group – there is no clear order of A, B, AB, and O blood types (although this could arguably be better treated as two indicator variables that interact, one for A antigen and one for B antigen).
12E2
An ordered logistic regression uses a cumulative logit link function rather than the ordinay logit link. The cumulative logit link uses the logit function applied to the cumulative probability of being in ordered category \(k\), i.e., \(P(y \leq k)\), instead of the probability that we observe a specific category, i.e., \(P(y = k)\).
12E3
When count data are zero-inflated, using a model that ignores zero-inflation will make the estimated mean look smaller than it is, because we include many zeros in the estimation of the mean that are not generated by the process with that mean.
12E4
A process that might produce over-dispersed counts is disease transmission when particular infected individuals have a chance of being superspreaders. On average, we would expect a particular person to infect a certain number of individuals, but superspreaders infect far more people than most infected individuals, increasing the variance in the case counts we observe.
A process that might show under-dispersion is one where there is a limit to the number of events that can occur per day. For example, if a small clinic has to ration vaccines and can give out at most \(k\) per day, if demand is high there will be consistently low variation in the number of vaccines distributed, although it could occasionally be lower so the variance is nonzero.
12M1
At this university, the ordinal employee ratings (1-4) were respectively 12, 36, 7, and 41. The cumulative log-odds of each ranking are \[ \log \frac{P(\text{rating} \leq k)}{1 - P(\text{rating} \leq k)}. \]
We can compute these like this.
counts <- c(12, 36, 7, 41)
probs <- counts / sum(counts)
c_probs <- cumsum(probs)
log(c_probs / (1 - c_probs))[1] -1.9459101 0.0000000 0.2937611 InfThe cumulative log-odds of the highest rating is infinite, because everyone was assigned a rating that is at most the highest value.
12M2
Let’s plot those cumulative ratings.
layout(1)
plot(
NULL, NULL,
type = "b",
xlab = "rating", ylab = "cumulative proportion",
xlim = c(1, length(counts)),
ylim = c(0, 1),
xaxt = "n"
)
axis(1, at = 1:4, labels = as.character(1:4))
d <- 0.0075
arrows(
x = 1:length(counts) - d,
x0 = 1:length(counts) - d,
y = c_probs,
y0 = 0,
length = 0,
col = "darkgray",
lwd = 2
)
arrows(
x = 1:length(counts) + d,
x0 = 1:length(counts) + d,
y = c_probs,
y0 = c_probs - probs,
length = 0,
lwd = 2, col = rethinking::rangi2
)
points(
1:length(counts),
c_probs,
type = "b", pch = 16, cex = 1.1
)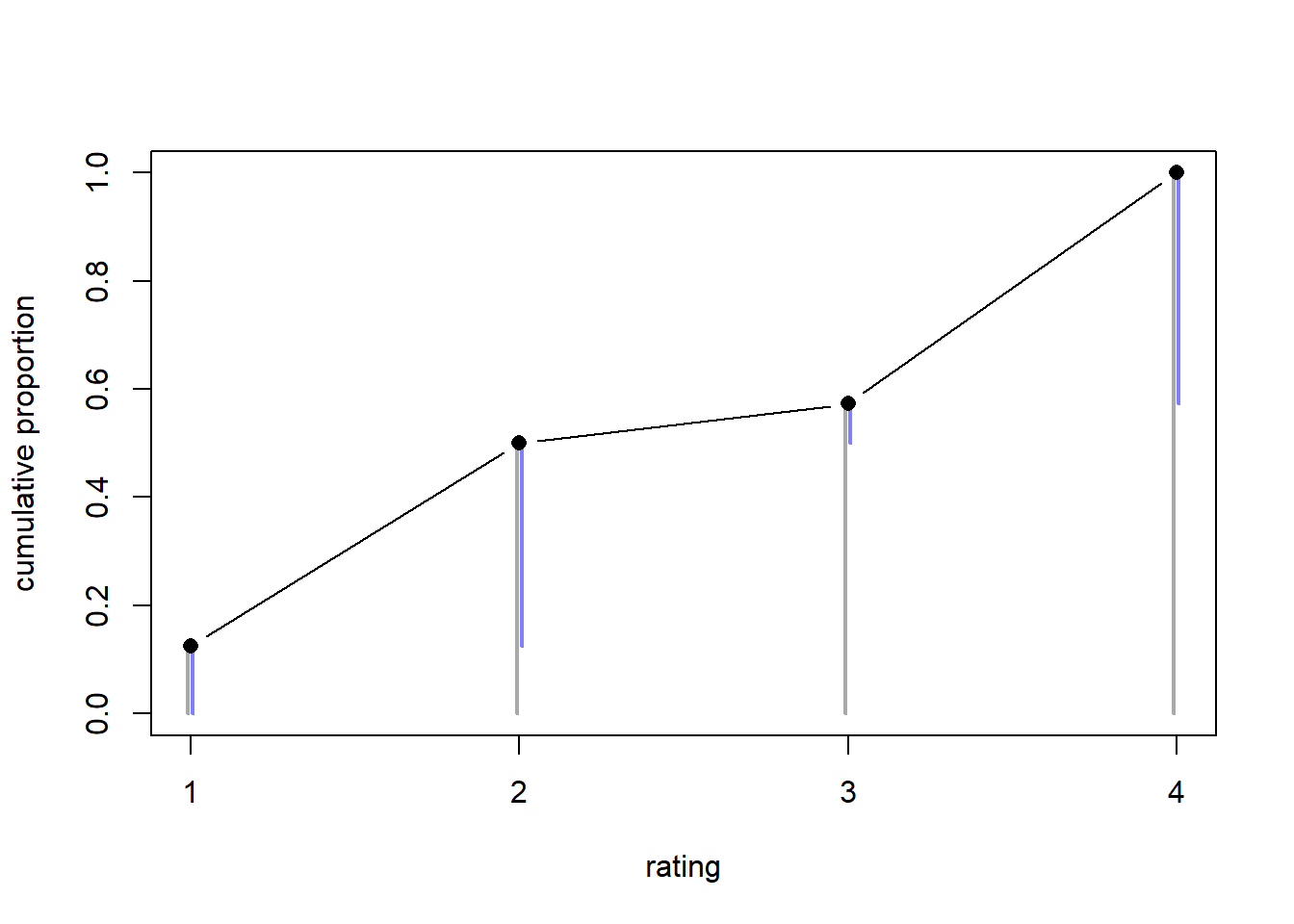
The points and the gray bars show the cumulative probability of a rating of \(k\) or higher, while the blue bars show the difference in probability between rating \(k\) and rating \(k-1\).
12M3
Earlier in the chapter, the zero-inflated Poisson likelihood was given as \[ (1-p)\left(\frac{\lambda^y\exp(-y)}{y!}\right). \]
We can write a similar zero-inflated binomial likelihood, we just can’t use the letter \(p\) twice. So let \(\pi\) be the probability that an observation is a zero from the process that only produces zeroes, and let \(n\) and \(p\) be the regular binomial parameters. Then,
\[ P(y \mid \pi, n, p) = \left(\pi \times 0 \right) + \left((1-\pi) \times \left( n \atop y \right) p ^ y\left(1 - p\right)^{n-y}\right), \] if \(y=1\), because all ones have to come from the binomial part, and \[ P(y \mid \pi, n, p) = \pi + \bigg((1- \pi) \times (1-p)^n\bigg) \] if \(y=0\) because a zero could be either from the zero-generating process or from the binomial part.
12H1
In this question we’ll examine the data for hurricane severity based on names.
data("Hurricanes", package = "rethinking")
dh <- list(
d = Hurricanes$deaths,
f = Hurricanes$femininity
)First we’ll fit a Poisson model that attempts to predict hurricane deaths based on the femininity score of the name.
m_12h1 <- rethinking::ulam(
alist(
d ~ dpois(lambda),
log(lambda) <- a + b * f,
a ~ dnorm(3, 0.5),
b ~ dnorm(0, 0.5)
),
data = dh,
chains = 4, cores = 4,
iter = 2500, warmup = 500
)Running MCMC with 4 parallel chains, with 1 thread(s) per chain...
Chain 1 Iteration: 1 / 2500 [ 0%] (Warmup)
Chain 1 Iteration: 100 / 2500 [ 4%] (Warmup)
Chain 1 Iteration: 200 / 2500 [ 8%] (Warmup)
Chain 1 Iteration: 300 / 2500 [ 12%] (Warmup)
Chain 1 Iteration: 400 / 2500 [ 16%] (Warmup)
Chain 1 Iteration: 500 / 2500 [ 20%] (Warmup)
Chain 1 Iteration: 501 / 2500 [ 20%] (Sampling)
Chain 1 Iteration: 600 / 2500 [ 24%] (Sampling)
Chain 1 Iteration: 700 / 2500 [ 28%] (Sampling)
Chain 1 Iteration: 800 / 2500 [ 32%] (Sampling)
Chain 1 Iteration: 900 / 2500 [ 36%] (Sampling)
Chain 1 Iteration: 1000 / 2500 [ 40%] (Sampling)
Chain 2 Iteration: 1 / 2500 [ 0%] (Warmup)
Chain 2 Iteration: 100 / 2500 [ 4%] (Warmup)
Chain 2 Iteration: 200 / 2500 [ 8%] (Warmup)
Chain 2 Iteration: 300 / 2500 [ 12%] (Warmup)
Chain 2 Iteration: 400 / 2500 [ 16%] (Warmup)
Chain 2 Iteration: 500 / 2500 [ 20%] (Warmup)
Chain 2 Iteration: 501 / 2500 [ 20%] (Sampling)
Chain 2 Iteration: 600 / 2500 [ 24%] (Sampling)
Chain 2 Iteration: 700 / 2500 [ 28%] (Sampling)
Chain 2 Iteration: 800 / 2500 [ 32%] (Sampling)
Chain 3 Iteration: 1 / 2500 [ 0%] (Warmup)
Chain 3 Iteration: 100 / 2500 [ 4%] (Warmup)
Chain 3 Iteration: 200 / 2500 [ 8%] (Warmup)
Chain 3 Iteration: 300 / 2500 [ 12%] (Warmup)
Chain 3 Iteration: 400 / 2500 [ 16%] (Warmup)
Chain 3 Iteration: 500 / 2500 [ 20%] (Warmup)
Chain 3 Iteration: 501 / 2500 [ 20%] (Sampling)
Chain 3 Iteration: 600 / 2500 [ 24%] (Sampling)
Chain 3 Iteration: 700 / 2500 [ 28%] (Sampling)
Chain 3 Iteration: 800 / 2500 [ 32%] (Sampling)
Chain 4 Iteration: 1 / 2500 [ 0%] (Warmup)
Chain 4 Iteration: 100 / 2500 [ 4%] (Warmup)
Chain 4 Iteration: 200 / 2500 [ 8%] (Warmup)
Chain 4 Iteration: 300 / 2500 [ 12%] (Warmup)
Chain 4 Iteration: 400 / 2500 [ 16%] (Warmup)
Chain 4 Iteration: 500 / 2500 [ 20%] (Warmup)
Chain 4 Iteration: 501 / 2500 [ 20%] (Sampling)
Chain 4 Iteration: 600 / 2500 [ 24%] (Sampling)
Chain 4 Iteration: 700 / 2500 [ 28%] (Sampling)
Chain 1 Iteration: 1100 / 2500 [ 44%] (Sampling)
Chain 1 Iteration: 1200 / 2500 [ 48%] (Sampling)
Chain 1 Iteration: 1300 / 2500 [ 52%] (Sampling)
Chain 1 Iteration: 1400 / 2500 [ 56%] (Sampling)
Chain 1 Iteration: 1500 / 2500 [ 60%] (Sampling)
Chain 1 Iteration: 1600 / 2500 [ 64%] (Sampling)
Chain 1 Iteration: 1700 / 2500 [ 68%] (Sampling)
Chain 1 Iteration: 1800 / 2500 [ 72%] (Sampling)
Chain 1 Iteration: 1900 / 2500 [ 76%] (Sampling)
Chain 1 Iteration: 2000 / 2500 [ 80%] (Sampling)
Chain 1 Iteration: 2100 / 2500 [ 84%] (Sampling)
Chain 1 Iteration: 2200 / 2500 [ 88%] (Sampling)
Chain 1 Iteration: 2300 / 2500 [ 92%] (Sampling)
Chain 1 Iteration: 2400 / 2500 [ 96%] (Sampling)
Chain 1 Iteration: 2500 / 2500 [100%] (Sampling)
Chain 1 finished in 0.3 seconds.
Chain 2 Iteration: 900 / 2500 [ 36%] (Sampling)
Chain 2 Iteration: 1000 / 2500 [ 40%] (Sampling)
Chain 2 Iteration: 1100 / 2500 [ 44%] (Sampling)
Chain 2 Iteration: 1200 / 2500 [ 48%] (Sampling)
Chain 2 Iteration: 1300 / 2500 [ 52%] (Sampling)
Chain 2 Iteration: 1400 / 2500 [ 56%] (Sampling)
Chain 2 Iteration: 1500 / 2500 [ 60%] (Sampling)
Chain 2 Iteration: 1600 / 2500 [ 64%] (Sampling)
Chain 2 Iteration: 1700 / 2500 [ 68%] (Sampling)
Chain 2 Iteration: 1800 / 2500 [ 72%] (Sampling)
Chain 2 Iteration: 1900 / 2500 [ 76%] (Sampling)
Chain 2 Iteration: 2000 / 2500 [ 80%] (Sampling)
Chain 2 Iteration: 2100 / 2500 [ 84%] (Sampling)
Chain 2 Iteration: 2200 / 2500 [ 88%] (Sampling)
Chain 2 Iteration: 2300 / 2500 [ 92%] (Sampling)
Chain 2 Iteration: 2400 / 2500 [ 96%] (Sampling)
Chain 2 Iteration: 2500 / 2500 [100%] (Sampling)
Chain 2 finished in 0.3 seconds.
Chain 3 Iteration: 900 / 2500 [ 36%] (Sampling)
Chain 3 Iteration: 1000 / 2500 [ 40%] (Sampling)
Chain 3 Iteration: 1100 / 2500 [ 44%] (Sampling)
Chain 3 Iteration: 1200 / 2500 [ 48%] (Sampling)
Chain 3 Iteration: 1300 / 2500 [ 52%] (Sampling)
Chain 3 Iteration: 1400 / 2500 [ 56%] (Sampling)
Chain 3 Iteration: 1500 / 2500 [ 60%] (Sampling)
Chain 3 Iteration: 1600 / 2500 [ 64%] (Sampling)
Chain 3 Iteration: 1700 / 2500 [ 68%] (Sampling)
Chain 3 Iteration: 1800 / 2500 [ 72%] (Sampling)
Chain 3 Iteration: 1900 / 2500 [ 76%] (Sampling)
Chain 3 Iteration: 2000 / 2500 [ 80%] (Sampling)
Chain 3 Iteration: 2100 / 2500 [ 84%] (Sampling)
Chain 3 Iteration: 2200 / 2500 [ 88%] (Sampling)
Chain 3 Iteration: 2300 / 2500 [ 92%] (Sampling)
Chain 3 Iteration: 2400 / 2500 [ 96%] (Sampling)
Chain 3 Iteration: 2500 / 2500 [100%] (Sampling)
Chain 3 finished in 0.3 seconds.
Chain 4 Iteration: 800 / 2500 [ 32%] (Sampling)
Chain 4 Iteration: 900 / 2500 [ 36%] (Sampling)
Chain 4 Iteration: 1000 / 2500 [ 40%] (Sampling)
Chain 4 Iteration: 1100 / 2500 [ 44%] (Sampling)
Chain 4 Iteration: 1200 / 2500 [ 48%] (Sampling)
Chain 4 Iteration: 1300 / 2500 [ 52%] (Sampling)
Chain 4 Iteration: 1400 / 2500 [ 56%] (Sampling)
Chain 4 Iteration: 1500 / 2500 [ 60%] (Sampling)
Chain 4 Iteration: 1600 / 2500 [ 64%] (Sampling)
Chain 4 Iteration: 1700 / 2500 [ 68%] (Sampling)
Chain 4 Iteration: 1800 / 2500 [ 72%] (Sampling)
Chain 4 Iteration: 1900 / 2500 [ 76%] (Sampling)
Chain 4 Iteration: 2000 / 2500 [ 80%] (Sampling)
Chain 4 Iteration: 2100 / 2500 [ 84%] (Sampling)
Chain 4 Iteration: 2200 / 2500 [ 88%] (Sampling)
Chain 4 Iteration: 2300 / 2500 [ 92%] (Sampling)
Chain 4 Iteration: 2400 / 2500 [ 96%] (Sampling)
Chain 4 Iteration: 2500 / 2500 [100%] (Sampling)
Chain 4 finished in 0.3 seconds.
All 4 chains finished successfully.
Mean chain execution time: 0.3 seconds.
Total execution time: 0.5 seconds.rethinking::precis(m_12h1) mean sd 5.5% 94.5% rhat ess_bulk
a 2.50609275 0.063863874 2.40280835 2.60604275 1.003211 1686.506
b 0.07315003 0.007949303 0.06051949 0.08596864 1.002717 1737.373We can see a positive effect of femininity on hurricane deaths from the \(b\) coefficient in the model. Now we want to get the predictions for each storm and check which storms are predicted well and which are predicted poorly.
link_12h1 <- rethinking::sim(m_12h1)
mean_12h1 <- colMeans(link_12h1)
pi_12h1 <- apply(link_12h1, 2, rethinking::PI)
layout(matrix(1:2, nrow = 1))
plot(
NULL, NULL,
xlim = c(1, nrow(Hurricanes)),
ylim = range(Hurricanes$deaths),
xlab = "Storm",
ylab = "Deaths",
axes = FALSE
)
axis(
1, at = 1:nrow(Hurricanes), labels = Hurricanes$name,
las = 2, cex.axis = 0.5
)
axis(2, at = seq(0, 250, 50))
arrows(
x = 1:nrow(Hurricanes),
x0 = 1:nrow(Hurricanes),
y = pi_12h1[1, ],
y0 = pi_12h1[2, ],
lwd = 2,
length = 0
)
points(
x = 1:nrow(Hurricanes),
y = mean_12h1
)
points(
x = 1:nrow(Hurricanes),
y = Hurricanes$deaths,
col = rethinking::rangi2,
pch = 4,
lwd = 1.25
)
# femininity plot
f_seq <- seq(1, 11, 0.01)
link_12h1_fem <- rethinking::sim(
m_12h1,
data = data.frame(f = f_seq)
)
mean_12h1_fem <- colMeans(link_12h1_fem)
pi_12h1_fem <- apply(link_12h1_fem, 2, rethinking::PI)
plot(
Hurricanes$femininity,
Hurricanes$deaths,
xlab = "Femininity of storm name",
ylab = "Deaths",
axes = FALSE,
xlim = c(1, 11),
ylim = range(Hurricanes$deaths)
)
axis(
1, at = seq(1, 11, 1)
)
axis(2, at = seq(0, 250, 50))
shade(pi_12h1_fem, f_seq)
lines(f_seq, mean_12h1_fem, lwd = 1.5)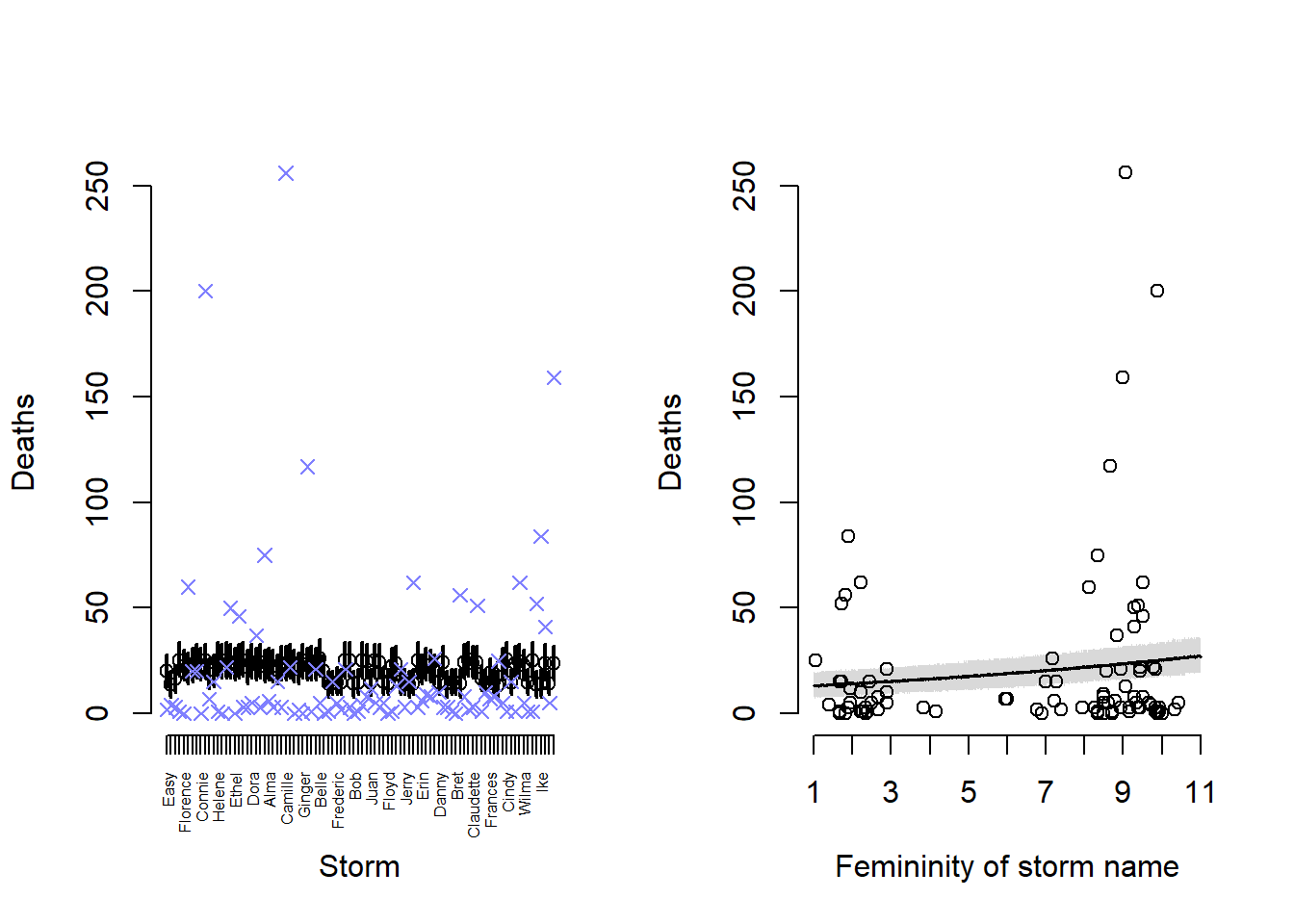
In the left plot plot, the circle and line shows the mean and 89% credible interval for the predicted number of deaths from a given hurricane. The blue x shows the observed number of deaths. We can see that almost all of the predictions are quite bad – it looks like the predictions are driven upwards by a few intense storms, but that makes the predictions of the least deadly storms bad as well. So other than a few storms with intermediate deaths, our predictions are pretty bad.
In the right plot, we can see that the predicted deaths by femininity score have a small credible itnerval, but almost all of the actual observed data points lie outside of the model prediction interval.
12H2
Since we saw more variability than the Poisson model expected, we’ll also fit a gamma-Poisson model for deaths predicted by name femininity.
m_12h2 <- rethinking::ulam(
alist(
d ~ dgampois(lambda, phi),
log(lambda) <- a + b * f,
a ~ dnorm(3, 0.5),
b ~ dnorm(0, 0.5),
phi ~ dexp(1)
),
data = dh,
chains = 4, cores = 4
)Running MCMC with 4 parallel chains, with 1 thread(s) per chain...
Chain 1 Iteration: 1 / 1000 [ 0%] (Warmup)
Chain 1 Iteration: 100 / 1000 [ 10%] (Warmup)
Chain 1 Iteration: 200 / 1000 [ 20%] (Warmup) Chain 2 Iteration: 1 / 1000 [ 0%] (Warmup)
Chain 2 Iteration: 100 / 1000 [ 10%] (Warmup) Chain 3 Iteration: 1 / 1000 [ 0%] (Warmup)
Chain 3 Iteration: 100 / 1000 [ 10%] (Warmup) Chain 4 Iteration: 1 / 1000 [ 0%] (Warmup) Chain 1 Iteration: 300 / 1000 [ 30%] (Warmup)
Chain 1 Iteration: 400 / 1000 [ 40%] (Warmup)
Chain 1 Iteration: 500 / 1000 [ 50%] (Warmup)
Chain 1 Iteration: 501 / 1000 [ 50%] (Sampling)
Chain 1 Iteration: 600 / 1000 [ 60%] (Sampling)
Chain 1 Iteration: 700 / 1000 [ 70%] (Sampling)
Chain 1 Iteration: 800 / 1000 [ 80%] (Sampling)
Chain 1 Iteration: 900 / 1000 [ 90%] (Sampling)
Chain 1 Iteration: 1000 / 1000 [100%] (Sampling)
Chain 2 Iteration: 200 / 1000 [ 20%] (Warmup)
Chain 2 Iteration: 300 / 1000 [ 30%] (Warmup)
Chain 2 Iteration: 400 / 1000 [ 40%] (Warmup)
Chain 2 Iteration: 500 / 1000 [ 50%] (Warmup)
Chain 2 Iteration: 501 / 1000 [ 50%] (Sampling)
Chain 2 Iteration: 600 / 1000 [ 60%] (Sampling)
Chain 2 Iteration: 700 / 1000 [ 70%] (Sampling)
Chain 2 Iteration: 800 / 1000 [ 80%] (Sampling)
Chain 2 Iteration: 900 / 1000 [ 90%] (Sampling)
Chain 3 Iteration: 200 / 1000 [ 20%] (Warmup)
Chain 3 Iteration: 300 / 1000 [ 30%] (Warmup)
Chain 3 Iteration: 400 / 1000 [ 40%] (Warmup)
Chain 3 Iteration: 500 / 1000 [ 50%] (Warmup)
Chain 3 Iteration: 501 / 1000 [ 50%] (Sampling)
Chain 3 Iteration: 600 / 1000 [ 60%] (Sampling)
Chain 3 Iteration: 700 / 1000 [ 70%] (Sampling)
Chain 3 Iteration: 800 / 1000 [ 80%] (Sampling)
Chain 3 Iteration: 900 / 1000 [ 90%] (Sampling)
Chain 3 Iteration: 1000 / 1000 [100%] (Sampling)
Chain 4 Iteration: 100 / 1000 [ 10%] (Warmup)
Chain 4 Iteration: 200 / 1000 [ 20%] (Warmup)
Chain 4 Iteration: 300 / 1000 [ 30%] (Warmup)
Chain 4 Iteration: 400 / 1000 [ 40%] (Warmup)
Chain 4 Iteration: 500 / 1000 [ 50%] (Warmup)
Chain 4 Iteration: 501 / 1000 [ 50%] (Sampling)
Chain 4 Iteration: 600 / 1000 [ 60%] (Sampling)
Chain 4 Iteration: 700 / 1000 [ 70%] (Sampling)
Chain 4 Iteration: 800 / 1000 [ 80%] (Sampling)
Chain 1 finished in 0.4 seconds.
Chain 2 Iteration: 1000 / 1000 [100%] (Sampling)
Chain 2 finished in 0.5 seconds.
Chain 3 finished in 0.4 seconds.
Chain 4 Iteration: 900 / 1000 [ 90%] (Sampling)
Chain 4 Iteration: 1000 / 1000 [100%] (Sampling)
Chain 4 finished in 0.5 seconds.
All 4 chains finished successfully.
Mean chain execution time: 0.4 seconds.
Total execution time: 0.6 seconds.rethinking::precis(m_12h2) mean sd 5.5% 94.5% rhat ess_bulk
a 2.72489273 0.30401777 2.25427495 3.2432744 1.001376 836.6150
b 0.04888609 0.04054782 -0.01808457 0.1126781 1.004221 814.0412
phi 0.45203219 0.06218637 0.35983162 0.5525003 1.004213 1055.6782In this model, we can see the model is no longer confident in the association between femininity and deaths, because the credible interval for \(b\) is now much wider and the SD is much closer to the mean. We also see that the estimated \(\phi\) is less than one, fairly small, which indicates that our data are overdispersed. Let’s plot the predictions again.
link_12h2 <- rethinking::sim(m_12h2)
mean_12h2 <- colMeans(link_12h2)
pi_12h2 <- apply(link_12h2, 2, rethinking::PI)
layout(matrix(1:2, nrow = 1))
plot(
NULL, NULL,
xlim = c(1, nrow(Hurricanes)),
ylim = range(Hurricanes$deaths),
xlab = "Storm",
ylab = "Deaths",
axes = FALSE
)
axis(
1, at = 1:nrow(Hurricanes), labels = Hurricanes$name,
las = 2, cex.axis = 0.5
)
axis(2, at = seq(0, 250, 50))
arrows(
x = 1:nrow(Hurricanes),
x0 = 1:nrow(Hurricanes),
y = pi_12h2[1, ],
y0 = pi_12h2[2, ],
lwd = 2,
length = 0
)
points(
x = 1:nrow(Hurricanes),
y = mean_12h2
)
points(
x = 1:nrow(Hurricanes),
y = Hurricanes$deaths,
col = rethinking::rangi2,
pch = 4,
lwd = 1.25
)
# femininity plot
f_seq <- seq(1, 11, 0.01)
link_12h2_fem <- rethinking::sim(
m_12h2,
data = data.frame(f = f_seq)
)
mean_12h2_fem <- colMeans(link_12h2_fem)
pi_12h2_fem <- apply(link_12h2_fem, 2, rethinking::PI)
plot(
Hurricanes$femininity,
Hurricanes$deaths,
xlab = "Femininity of storm name",
ylab = "Deaths",
axes = FALSE,
xlim = c(1, 11),
ylim = range(Hurricanes$deaths)
)
axis(
1, at = seq(1, 11, 1)
)
axis(2, at = seq(0, 250, 50))
shade(pi_12h2_fem, f_seq)
lines(f_seq, mean_12h2_fem, lwd = 1.5)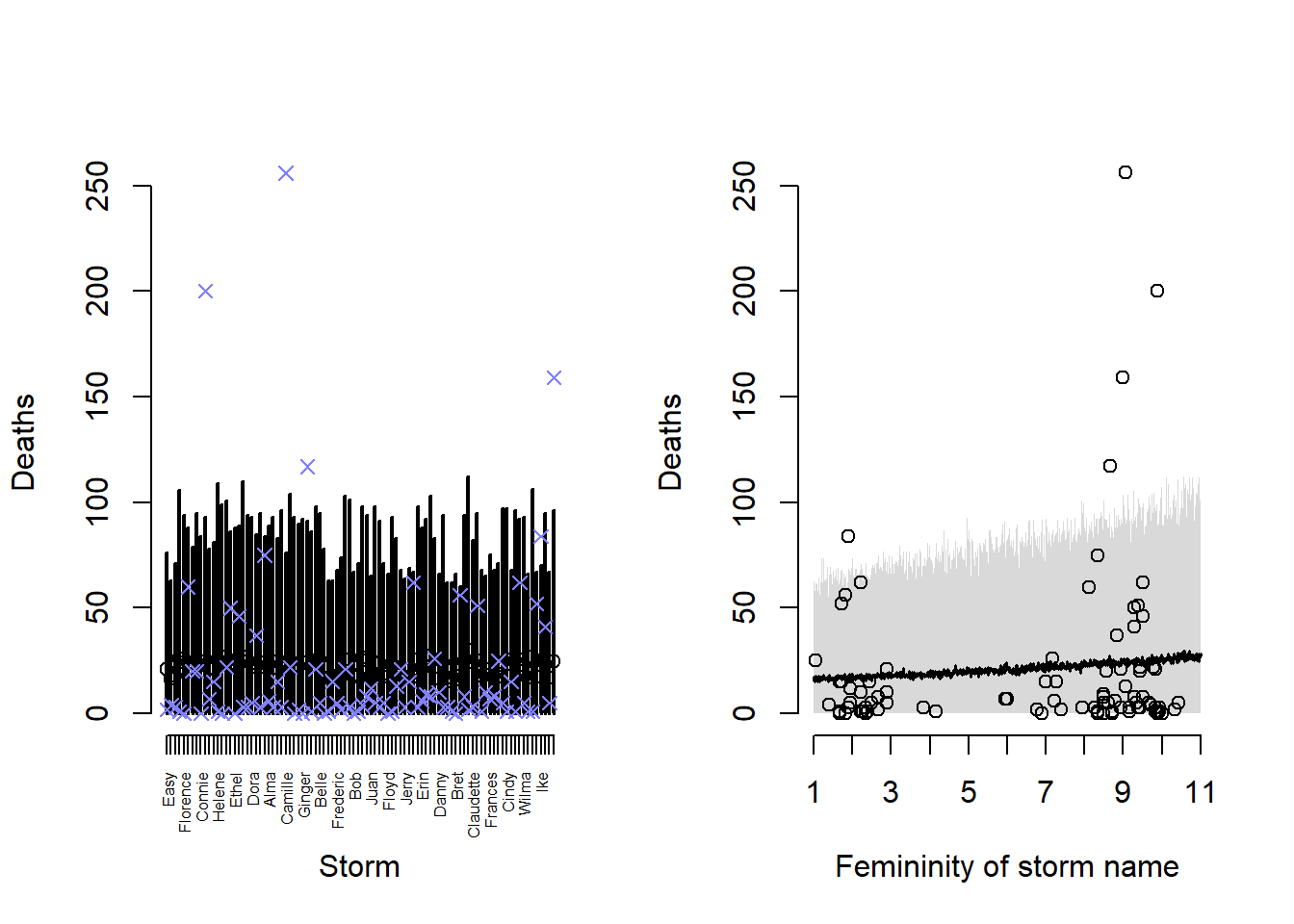
In this model, we can see that the variance of our predictions is much larger, and we can thus capture many more of the storms that our previous model failed to predict. In this model, the variance we estimated in the deaths per hurricane dominates any potential effect of name femininity and it seems that variance is the more important aspect here. There are still a few very extreme storms that we fail to predict with our prediction intervals, though.
12H3
Now we’ll include damage_norm and min_pressure in our model, two meterological variables that can predict the potential of a hurricane to cause damage. We’ll allow both of them to interact with femininity to see if hurricanes with feminine names are actually what is important. I’ll fit two models: one with the interactions, and one that doesn’t have any of the femininity terms in it. Probably it would be better to build every combination of interaction/non-interaction models with all 3 possible combinations of the meterological variables but I am not going to do that for now.
Note that I had to standardize the three variables to get consistent Stan initializations here.
dh2 <- dh
dh2$f <- standardize(Hurricanes$femininity)
dh2$dn <- standardize(Hurricanes$damage_norm)
dh2$mp <- standardize(Hurricanes$min_pressure)First we’ll fit the model with all the interactions.
m_12h3_a <- rethinking::ulam(
alist(
d ~ dgampois(lambda, phi),
log(lambda) <- a + bf * f + bd * dn + bp * mp +
gfd * f * dn + gfp * f * mp,
a ~ dnorm(3, 0.5),
bf ~ dnorm(0, 0.5),
bd ~ dnorm(0, 0.5),
bp ~ dnorm(0, 0.5),
gfd ~ dnorm(0, 0.25),
gfp ~ dnorm(0, 0.25),
phi ~ dexp(1)
),
data = dh2,
chains = 4, cores = 4,
iter = 2500, warmup = 500,
log_lik = TRUE
)Running MCMC with 4 parallel chains, with 1 thread(s) per chain...
Chain 1 Iteration: 1 / 2500 [ 0%] (Warmup)
Chain 1 Iteration: 100 / 2500 [ 4%] (Warmup)
Chain 1 Iteration: 200 / 2500 [ 8%] (Warmup) Chain 2 Iteration: 1 / 2500 [ 0%] (Warmup)
Chain 2 Iteration: 100 / 2500 [ 4%] (Warmup) Chain 3 Iteration: 1 / 2500 [ 0%] (Warmup)
Chain 3 Iteration: 100 / 2500 [ 4%] (Warmup) Chain 4 Iteration: 1 / 2500 [ 0%] (Warmup)
Chain 4 Iteration: 100 / 2500 [ 4%] (Warmup) Chain 1 Iteration: 300 / 2500 [ 12%] (Warmup)
Chain 1 Iteration: 400 / 2500 [ 16%] (Warmup)
Chain 1 Iteration: 500 / 2500 [ 20%] (Warmup)
Chain 1 Iteration: 501 / 2500 [ 20%] (Sampling)
Chain 1 Iteration: 600 / 2500 [ 24%] (Sampling)
Chain 1 Iteration: 700 / 2500 [ 28%] (Sampling)
Chain 1 Iteration: 800 / 2500 [ 32%] (Sampling)
Chain 2 Iteration: 200 / 2500 [ 8%] (Warmup)
Chain 2 Iteration: 300 / 2500 [ 12%] (Warmup)
Chain 2 Iteration: 400 / 2500 [ 16%] (Warmup)
Chain 2 Iteration: 500 / 2500 [ 20%] (Warmup)
Chain 2 Iteration: 501 / 2500 [ 20%] (Sampling)
Chain 2 Iteration: 600 / 2500 [ 24%] (Sampling)
Chain 2 Iteration: 700 / 2500 [ 28%] (Sampling)
Chain 3 Iteration: 200 / 2500 [ 8%] (Warmup)
Chain 3 Iteration: 300 / 2500 [ 12%] (Warmup)
Chain 3 Iteration: 400 / 2500 [ 16%] (Warmup)
Chain 3 Iteration: 500 / 2500 [ 20%] (Warmup)
Chain 3 Iteration: 501 / 2500 [ 20%] (Sampling)
Chain 3 Iteration: 600 / 2500 [ 24%] (Sampling)
Chain 3 Iteration: 700 / 2500 [ 28%] (Sampling)
Chain 4 Iteration: 200 / 2500 [ 8%] (Warmup)
Chain 4 Iteration: 300 / 2500 [ 12%] (Warmup)
Chain 4 Iteration: 400 / 2500 [ 16%] (Warmup)
Chain 4 Iteration: 500 / 2500 [ 20%] (Warmup)
Chain 4 Iteration: 501 / 2500 [ 20%] (Sampling)
Chain 4 Iteration: 600 / 2500 [ 24%] (Sampling)
Chain 4 Iteration: 700 / 2500 [ 28%] (Sampling)
Chain 4 Iteration: 800 / 2500 [ 32%] (Sampling)
Chain 1 Iteration: 900 / 2500 [ 36%] (Sampling)
Chain 1 Iteration: 1000 / 2500 [ 40%] (Sampling)
Chain 1 Iteration: 1100 / 2500 [ 44%] (Sampling)
Chain 2 Iteration: 800 / 2500 [ 32%] (Sampling)
Chain 2 Iteration: 900 / 2500 [ 36%] (Sampling)
Chain 2 Iteration: 1000 / 2500 [ 40%] (Sampling)
Chain 3 Iteration: 800 / 2500 [ 32%] (Sampling)
Chain 3 Iteration: 900 / 2500 [ 36%] (Sampling)
Chain 3 Iteration: 1000 / 2500 [ 40%] (Sampling)
Chain 4 Iteration: 900 / 2500 [ 36%] (Sampling)
Chain 4 Iteration: 1000 / 2500 [ 40%] (Sampling)
Chain 1 Iteration: 1200 / 2500 [ 48%] (Sampling)
Chain 1 Iteration: 1300 / 2500 [ 52%] (Sampling)
Chain 2 Iteration: 1100 / 2500 [ 44%] (Sampling)
Chain 2 Iteration: 1200 / 2500 [ 48%] (Sampling)
Chain 3 Iteration: 1100 / 2500 [ 44%] (Sampling)
Chain 3 Iteration: 1200 / 2500 [ 48%] (Sampling)
Chain 4 Iteration: 1100 / 2500 [ 44%] (Sampling)
Chain 4 Iteration: 1200 / 2500 [ 48%] (Sampling)
Chain 4 Iteration: 1300 / 2500 [ 52%] (Sampling)
Chain 1 Iteration: 1400 / 2500 [ 56%] (Sampling)
Chain 1 Iteration: 1500 / 2500 [ 60%] (Sampling)
Chain 1 Iteration: 1600 / 2500 [ 64%] (Sampling)
Chain 2 Iteration: 1300 / 2500 [ 52%] (Sampling)
Chain 2 Iteration: 1400 / 2500 [ 56%] (Sampling)
Chain 3 Iteration: 1300 / 2500 [ 52%] (Sampling)
Chain 3 Iteration: 1400 / 2500 [ 56%] (Sampling)
Chain 4 Iteration: 1400 / 2500 [ 56%] (Sampling)
Chain 4 Iteration: 1500 / 2500 [ 60%] (Sampling)
Chain 1 Iteration: 1700 / 2500 [ 68%] (Sampling)
Chain 1 Iteration: 1800 / 2500 [ 72%] (Sampling)
Chain 2 Iteration: 1500 / 2500 [ 60%] (Sampling)
Chain 2 Iteration: 1600 / 2500 [ 64%] (Sampling)
Chain 2 Iteration: 1700 / 2500 [ 68%] (Sampling)
Chain 3 Iteration: 1500 / 2500 [ 60%] (Sampling)
Chain 3 Iteration: 1600 / 2500 [ 64%] (Sampling)
Chain 4 Iteration: 1600 / 2500 [ 64%] (Sampling)
Chain 4 Iteration: 1700 / 2500 [ 68%] (Sampling)
Chain 4 Iteration: 1800 / 2500 [ 72%] (Sampling)
Chain 1 Iteration: 1900 / 2500 [ 76%] (Sampling)
Chain 1 Iteration: 2000 / 2500 [ 80%] (Sampling)
Chain 2 Iteration: 1800 / 2500 [ 72%] (Sampling)
Chain 2 Iteration: 1900 / 2500 [ 76%] (Sampling)
Chain 3 Iteration: 1700 / 2500 [ 68%] (Sampling)
Chain 3 Iteration: 1800 / 2500 [ 72%] (Sampling)
Chain 3 Iteration: 1900 / 2500 [ 76%] (Sampling)
Chain 4 Iteration: 1900 / 2500 [ 76%] (Sampling)
Chain 4 Iteration: 2000 / 2500 [ 80%] (Sampling)
Chain 1 Iteration: 2100 / 2500 [ 84%] (Sampling)
Chain 1 Iteration: 2200 / 2500 [ 88%] (Sampling)
Chain 1 Iteration: 2300 / 2500 [ 92%] (Sampling)
Chain 2 Iteration: 2000 / 2500 [ 80%] (Sampling)
Chain 2 Iteration: 2100 / 2500 [ 84%] (Sampling)
Chain 3 Iteration: 2000 / 2500 [ 80%] (Sampling)
Chain 3 Iteration: 2100 / 2500 [ 84%] (Sampling)
Chain 4 Iteration: 2100 / 2500 [ 84%] (Sampling)
Chain 4 Iteration: 2200 / 2500 [ 88%] (Sampling)
Chain 1 Iteration: 2400 / 2500 [ 96%] (Sampling)
Chain 1 Iteration: 2500 / 2500 [100%] (Sampling)
Chain 2 Iteration: 2200 / 2500 [ 88%] (Sampling)
Chain 2 Iteration: 2300 / 2500 [ 92%] (Sampling)
Chain 2 Iteration: 2400 / 2500 [ 96%] (Sampling)
Chain 3 Iteration: 2200 / 2500 [ 88%] (Sampling)
Chain 3 Iteration: 2300 / 2500 [ 92%] (Sampling)
Chain 4 Iteration: 2300 / 2500 [ 92%] (Sampling)
Chain 4 Iteration: 2400 / 2500 [ 96%] (Sampling)
Chain 4 Iteration: 2500 / 2500 [100%] (Sampling)
Chain 1 finished in 1.2 seconds.
Chain 4 finished in 1.2 seconds.
Chain 2 Iteration: 2500 / 2500 [100%] (Sampling)
Chain 3 Iteration: 2400 / 2500 [ 96%] (Sampling)
Chain 3 Iteration: 2500 / 2500 [100%] (Sampling)
Chain 2 finished in 1.3 seconds.
Chain 3 finished in 1.3 seconds.
All 4 chains finished successfully.
Mean chain execution time: 1.3 seconds.
Total execution time: 1.4 seconds.rethinking::precis(m_12h3_a) mean sd 5.5% 94.5% rhat ess_bulk
a 2.5745349 0.1301424 2.37077580 2.7872022 0.9998822 7799.679
bf 0.1205388 0.1229688 -0.08189045 0.3112198 1.0008055 9047.224
bd 0.8424011 0.2002610 0.53184151 1.1730111 1.0002519 7689.503
bp -0.4267335 0.1435744 -0.65813515 -0.1985004 1.0009340 6971.105
gfd 0.3157361 0.1674283 0.04206050 0.5792977 1.0002878 6890.718
gfp 0.1903824 0.1399754 -0.03370883 0.4133424 1.0014335 6520.778
phi 0.7335337 0.1128152 0.56546355 0.9239763 1.0008624 8391.883And now we’ll fit the model without femininity.
m_12h3_b <- rethinking::ulam(
alist(
d ~ dgampois(lambda, phi),
log(lambda) <- a + bd * dn + bp * mp,
a ~ dnorm(3, 0.5),
bd ~ dnorm(0, 0.5),
bp ~ dnorm(0, 0.5),
phi ~ dexp(1)
),
data = dh2,
chains = 4, cores = 4,
iter = 2500, warmup = 500,
log_lik = TRUE
)Running MCMC with 4 parallel chains, with 1 thread(s) per chain...
Chain 1 Iteration: 1 / 2500 [ 0%] (Warmup)
Chain 1 Iteration: 100 / 2500 [ 4%] (Warmup)
Chain 1 Iteration: 200 / 2500 [ 8%] (Warmup)
Chain 1 Iteration: 300 / 2500 [ 12%] (Warmup) Chain 2 Iteration: 1 / 2500 [ 0%] (Warmup)
Chain 2 Iteration: 100 / 2500 [ 4%] (Warmup)
Chain 2 Iteration: 200 / 2500 [ 8%] (Warmup)
Chain 2 Iteration: 300 / 2500 [ 12%] (Warmup) Chain 3 Iteration: 1 / 2500 [ 0%] (Warmup)
Chain 3 Iteration: 100 / 2500 [ 4%] (Warmup)
Chain 3 Iteration: 200 / 2500 [ 8%] (Warmup) Chain 4 Iteration: 1 / 2500 [ 0%] (Warmup)
Chain 4 Iteration: 100 / 2500 [ 4%] (Warmup)
Chain 4 Iteration: 200 / 2500 [ 8%] (Warmup) Chain 1 Iteration: 400 / 2500 [ 16%] (Warmup)
Chain 1 Iteration: 500 / 2500 [ 20%] (Warmup)
Chain 1 Iteration: 501 / 2500 [ 20%] (Sampling)
Chain 1 Iteration: 600 / 2500 [ 24%] (Sampling)
Chain 1 Iteration: 700 / 2500 [ 28%] (Sampling)
Chain 1 Iteration: 800 / 2500 [ 32%] (Sampling)
Chain 1 Iteration: 900 / 2500 [ 36%] (Sampling)
Chain 1 Iteration: 1000 / 2500 [ 40%] (Sampling)
Chain 2 Iteration: 400 / 2500 [ 16%] (Warmup)
Chain 2 Iteration: 500 / 2500 [ 20%] (Warmup)
Chain 2 Iteration: 501 / 2500 [ 20%] (Sampling)
Chain 2 Iteration: 600 / 2500 [ 24%] (Sampling)
Chain 2 Iteration: 700 / 2500 [ 28%] (Sampling)
Chain 2 Iteration: 800 / 2500 [ 32%] (Sampling)
Chain 2 Iteration: 900 / 2500 [ 36%] (Sampling)
Chain 2 Iteration: 1000 / 2500 [ 40%] (Sampling)
Chain 3 Iteration: 300 / 2500 [ 12%] (Warmup)
Chain 3 Iteration: 400 / 2500 [ 16%] (Warmup)
Chain 3 Iteration: 500 / 2500 [ 20%] (Warmup)
Chain 3 Iteration: 501 / 2500 [ 20%] (Sampling)
Chain 3 Iteration: 600 / 2500 [ 24%] (Sampling)
Chain 3 Iteration: 700 / 2500 [ 28%] (Sampling)
Chain 3 Iteration: 800 / 2500 [ 32%] (Sampling)
Chain 3 Iteration: 900 / 2500 [ 36%] (Sampling)
Chain 4 Iteration: 300 / 2500 [ 12%] (Warmup)
Chain 4 Iteration: 400 / 2500 [ 16%] (Warmup)
Chain 4 Iteration: 500 / 2500 [ 20%] (Warmup)
Chain 4 Iteration: 501 / 2500 [ 20%] (Sampling)
Chain 4 Iteration: 600 / 2500 [ 24%] (Sampling)
Chain 4 Iteration: 700 / 2500 [ 28%] (Sampling)
Chain 4 Iteration: 800 / 2500 [ 32%] (Sampling)
Chain 4 Iteration: 900 / 2500 [ 36%] (Sampling)
Chain 1 Iteration: 1100 / 2500 [ 44%] (Sampling)
Chain 1 Iteration: 1200 / 2500 [ 48%] (Sampling)
Chain 1 Iteration: 1300 / 2500 [ 52%] (Sampling)
Chain 2 Iteration: 1100 / 2500 [ 44%] (Sampling)
Chain 2 Iteration: 1200 / 2500 [ 48%] (Sampling)
Chain 2 Iteration: 1300 / 2500 [ 52%] (Sampling)
Chain 3 Iteration: 1000 / 2500 [ 40%] (Sampling)
Chain 3 Iteration: 1100 / 2500 [ 44%] (Sampling)
Chain 3 Iteration: 1200 / 2500 [ 48%] (Sampling)
Chain 3 Iteration: 1300 / 2500 [ 52%] (Sampling)
Chain 4 Iteration: 1000 / 2500 [ 40%] (Sampling)
Chain 4 Iteration: 1100 / 2500 [ 44%] (Sampling)
Chain 4 Iteration: 1200 / 2500 [ 48%] (Sampling)
Chain 1 Iteration: 1400 / 2500 [ 56%] (Sampling)
Chain 1 Iteration: 1500 / 2500 [ 60%] (Sampling)
Chain 2 Iteration: 1400 / 2500 [ 56%] (Sampling)
Chain 2 Iteration: 1500 / 2500 [ 60%] (Sampling)
Chain 2 Iteration: 1600 / 2500 [ 64%] (Sampling)
Chain 3 Iteration: 1400 / 2500 [ 56%] (Sampling)
Chain 3 Iteration: 1500 / 2500 [ 60%] (Sampling)
Chain 4 Iteration: 1300 / 2500 [ 52%] (Sampling)
Chain 4 Iteration: 1400 / 2500 [ 56%] (Sampling)
Chain 4 Iteration: 1500 / 2500 [ 60%] (Sampling)
Chain 1 Iteration: 1600 / 2500 [ 64%] (Sampling)
Chain 1 Iteration: 1700 / 2500 [ 68%] (Sampling)
Chain 1 Iteration: 1800 / 2500 [ 72%] (Sampling)
Chain 2 Iteration: 1700 / 2500 [ 68%] (Sampling)
Chain 2 Iteration: 1800 / 2500 [ 72%] (Sampling)
Chain 2 Iteration: 1900 / 2500 [ 76%] (Sampling)
Chain 3 Iteration: 1600 / 2500 [ 64%] (Sampling)
Chain 3 Iteration: 1700 / 2500 [ 68%] (Sampling)
Chain 3 Iteration: 1800 / 2500 [ 72%] (Sampling)
Chain 4 Iteration: 1600 / 2500 [ 64%] (Sampling)
Chain 4 Iteration: 1700 / 2500 [ 68%] (Sampling)
Chain 1 Iteration: 1900 / 2500 [ 76%] (Sampling)
Chain 1 Iteration: 2000 / 2500 [ 80%] (Sampling)
Chain 1 Iteration: 2100 / 2500 [ 84%] (Sampling)
Chain 2 Iteration: 2000 / 2500 [ 80%] (Sampling)
Chain 2 Iteration: 2100 / 2500 [ 84%] (Sampling)
Chain 3 Iteration: 1900 / 2500 [ 76%] (Sampling)
Chain 3 Iteration: 2000 / 2500 [ 80%] (Sampling)
Chain 4 Iteration: 1800 / 2500 [ 72%] (Sampling)
Chain 4 Iteration: 1900 / 2500 [ 76%] (Sampling)
Chain 4 Iteration: 2000 / 2500 [ 80%] (Sampling)
Chain 1 Iteration: 2200 / 2500 [ 88%] (Sampling)
Chain 1 Iteration: 2300 / 2500 [ 92%] (Sampling)
Chain 2 Iteration: 2200 / 2500 [ 88%] (Sampling)
Chain 2 Iteration: 2300 / 2500 [ 92%] (Sampling)
Chain 2 Iteration: 2400 / 2500 [ 96%] (Sampling)
Chain 3 Iteration: 2100 / 2500 [ 84%] (Sampling)
Chain 3 Iteration: 2200 / 2500 [ 88%] (Sampling)
Chain 3 Iteration: 2300 / 2500 [ 92%] (Sampling)
Chain 4 Iteration: 2100 / 2500 [ 84%] (Sampling)
Chain 4 Iteration: 2200 / 2500 [ 88%] (Sampling)
Chain 4 Iteration: 2300 / 2500 [ 92%] (Sampling)
Chain 1 Iteration: 2400 / 2500 [ 96%] (Sampling)
Chain 1 Iteration: 2500 / 2500 [100%] (Sampling)
Chain 2 Iteration: 2500 / 2500 [100%] (Sampling)
Chain 3 Iteration: 2400 / 2500 [ 96%] (Sampling)
Chain 3 Iteration: 2500 / 2500 [100%] (Sampling)
Chain 4 Iteration: 2400 / 2500 [ 96%] (Sampling)
Chain 4 Iteration: 2500 / 2500 [100%] (Sampling)
Chain 1 finished in 1.1 seconds.
Chain 2 finished in 1.0 seconds.
Chain 3 finished in 1.0 seconds.
Chain 4 finished in 1.0 seconds.
All 4 chains finished successfully.
Mean chain execution time: 1.0 seconds.
Total execution time: 1.2 seconds.rethinking::precis(m_12h3_b) mean sd 5.5% 94.5% rhat ess_bulk
a 2.5991976 0.1289468 2.4011245 2.8082190 1.0003433 8976.347
bd 0.9556939 0.2066803 0.6344573 1.2996627 1.0004285 8153.324
bp -0.3082165 0.1293662 -0.5170351 -0.1015891 0.9999208 9333.462
phi 0.6966203 0.1057378 0.5402283 0.8751461 1.0002122 8670.871Let’s compare the two models.
rethinking::compare(m_12h3_a, m_12h3_b, sort = "PSIS", func = PSIS) PSIS SE dPSIS dSE pPSIS weight
m_12h3_a 667.4475 36.12248 0.000000 NA 9.312312 0.8419216
m_12h3_b 670.7927 38.26946 3.345192 5.409417 7.875416 0.1580784Looks like the model with femininity in it doesn’t make noticeably better predictions than the model without femininity, although we have some very high Pareto \(k\) values, so this might be determined by some influential points.
Let’s make some counterfactual predictions like Richard suggests. Interpreting all three of our predictor variables at the same time can be quite difficult, but I’ll choose a medium, high, and low level of both meterological variables, and a high/low value of femininity.
Based on our previous plots, we can see that \(5\) is a good cutoff between two groups of names based on femininity. So we’ll use a femininity of \(2\) for masculine hurricane names, and a femininity of \(9\) for feminine hurricane names. Then we’ll choose our cutoffs for the (standardized) meterological variables as Q1, Q2, and Q3.
(dn_cutoffs <- quantile(dh2$dn, probs = c(0.25, 0.5, 0.75))) 25% 50% 75%
-0.54312166 -0.43449397 0.06902052 (mp_cutoffs <- quantile(dh2$mp, probs = c(0.25, 0.5, 0.75))) 25% 50% 75%
-0.78220741 -0.04789025 0.90934462 Now we can get our predictions from the model with interactions.
pred_data_f <- expand.grid(
f = c(9),
dn = unname(dn_cutoffs),
mp = unname(mp_cutoffs)
)
pred_data_m <- expand.grid(
f = c(2),
dn = unname(dn_cutoffs),
mp = unname(mp_cutoffs)
)
preds_12h3_f <- rethinking::sim(m_12h3_a, data = pred_data_f)
preds_12h3_m <- rethinking::sim(m_12h3_a, data = pred_data_m)
contr_12h3 <- preds_12h3_m - preds_12h3_f
contr_12h3_mean <- colMeans(contr_12h3)
contr_12h3_pi <- apply(contr_12h3, 2, rethinking::PI)
tibble::tibble(
"damage_norm" = c("L", "M", "H", "L", "M", "H", "L", "M", "H"),
"min_pressure" = c("L", "L", "L", "M", "M", "M", "H", "H", "H"),
"contrast (M - F)" = paste0(
formatC(contr_12h3_mean, digits = 2, format = "f"), " (",
formatC(contr_12h3_pi[1, ], digits = 0, format = "f"), ", ",
formatC(contr_12h3_pi[2, ], digits = 0, format = "f"), ")"
)
)# A tibble: 9 × 3
damage_norm min_pressure `contrast (M - F)`
<chr> <chr> <chr>
1 L L -0.06 (-25, 25)
2 M L -2.08 (-46, 36)
3 H L -0.02 (-13, 14)
4 L M -0.19 (-16, 15)
5 M M -0.03 (-16, 15)
6 H M 0.91 (-107, 106)
7 L H -0.07 (-33, 31)
8 M H 5.37 (-246, 253)
9 H H -0.18 (-26, 30) We can see that regardless of the combination of damage_norm and min_pressure, the difference in predicted deaths between masculine named and feminine named hurricanes has a huge range of predicted values, both negative and positive. So it really seems that there is no difference based on the hurricane names once we take the actual meterological variables into account – perhaps some hurricanes with feminine names were just coincidentally also more intense hurricanes.
12H4
OK, so for this problem we’ll compare the previous model with no femininity term to a model that’s the same but with damage_norm on the log scale.
dh2$log_dn <- standardize(log(Hurricanes$damage_norm))
m_12h4 <- rethinking::ulam(
alist(
d ~ dgampois(lambda, phi),
log(lambda) <- a + bd * log_dn + bp * mp,
a ~ dnorm(3, 0.5),
bd ~ dnorm(0, 0.5),
bp ~ dnorm(0, 0.5),
phi ~ dexp(1)
),
data = dh2,
chains = 4, cores = 4,
iter = 2500, warmup = 500,
log_lik = TRUE
)Running MCMC with 4 parallel chains, with 1 thread(s) per chain...
Chain 1 Iteration: 1 / 2500 [ 0%] (Warmup)
Chain 1 Iteration: 100 / 2500 [ 4%] (Warmup)
Chain 1 Iteration: 200 / 2500 [ 8%] (Warmup) Chain 2 Iteration: 1 / 2500 [ 0%] (Warmup)
Chain 2 Iteration: 100 / 2500 [ 4%] (Warmup)
Chain 2 Iteration: 200 / 2500 [ 8%] (Warmup) Chain 3 Iteration: 1 / 2500 [ 0%] (Warmup)
Chain 3 Iteration: 100 / 2500 [ 4%] (Warmup)
Chain 3 Iteration: 200 / 2500 [ 8%] (Warmup) Chain 4 Iteration: 1 / 2500 [ 0%] (Warmup)
Chain 4 Iteration: 100 / 2500 [ 4%] (Warmup)
Chain 4 Iteration: 200 / 2500 [ 8%] (Warmup) Chain 1 Iteration: 300 / 2500 [ 12%] (Warmup)
Chain 1 Iteration: 400 / 2500 [ 16%] (Warmup)
Chain 1 Iteration: 500 / 2500 [ 20%] (Warmup)
Chain 1 Iteration: 501 / 2500 [ 20%] (Sampling)
Chain 1 Iteration: 600 / 2500 [ 24%] (Sampling)
Chain 1 Iteration: 700 / 2500 [ 28%] (Sampling)
Chain 1 Iteration: 800 / 2500 [ 32%] (Sampling)
Chain 1 Iteration: 900 / 2500 [ 36%] (Sampling)
Chain 2 Iteration: 300 / 2500 [ 12%] (Warmup)
Chain 2 Iteration: 400 / 2500 [ 16%] (Warmup)
Chain 2 Iteration: 500 / 2500 [ 20%] (Warmup)
Chain 2 Iteration: 501 / 2500 [ 20%] (Sampling)
Chain 2 Iteration: 600 / 2500 [ 24%] (Sampling)
Chain 2 Iteration: 700 / 2500 [ 28%] (Sampling)
Chain 2 Iteration: 800 / 2500 [ 32%] (Sampling)
Chain 2 Iteration: 900 / 2500 [ 36%] (Sampling)
Chain 3 Iteration: 300 / 2500 [ 12%] (Warmup)
Chain 3 Iteration: 400 / 2500 [ 16%] (Warmup)
Chain 3 Iteration: 500 / 2500 [ 20%] (Warmup)
Chain 3 Iteration: 501 / 2500 [ 20%] (Sampling)
Chain 3 Iteration: 600 / 2500 [ 24%] (Sampling)
Chain 3 Iteration: 700 / 2500 [ 28%] (Sampling)
Chain 3 Iteration: 800 / 2500 [ 32%] (Sampling)
Chain 3 Iteration: 900 / 2500 [ 36%] (Sampling)
Chain 4 Iteration: 300 / 2500 [ 12%] (Warmup)
Chain 4 Iteration: 400 / 2500 [ 16%] (Warmup)
Chain 4 Iteration: 500 / 2500 [ 20%] (Warmup)
Chain 4 Iteration: 501 / 2500 [ 20%] (Sampling)
Chain 4 Iteration: 600 / 2500 [ 24%] (Sampling)
Chain 4 Iteration: 700 / 2500 [ 28%] (Sampling)
Chain 4 Iteration: 800 / 2500 [ 32%] (Sampling)
Chain 1 Iteration: 1000 / 2500 [ 40%] (Sampling)
Chain 1 Iteration: 1100 / 2500 [ 44%] (Sampling)
Chain 2 Iteration: 1000 / 2500 [ 40%] (Sampling)
Chain 2 Iteration: 1100 / 2500 [ 44%] (Sampling)
Chain 2 Iteration: 1200 / 2500 [ 48%] (Sampling)
Chain 3 Iteration: 1000 / 2500 [ 40%] (Sampling)
Chain 3 Iteration: 1100 / 2500 [ 44%] (Sampling)
Chain 3 Iteration: 1200 / 2500 [ 48%] (Sampling)
Chain 4 Iteration: 900 / 2500 [ 36%] (Sampling)
Chain 4 Iteration: 1000 / 2500 [ 40%] (Sampling)
Chain 4 Iteration: 1100 / 2500 [ 44%] (Sampling)
Chain 1 Iteration: 1200 / 2500 [ 48%] (Sampling)
Chain 1 Iteration: 1300 / 2500 [ 52%] (Sampling)
Chain 1 Iteration: 1400 / 2500 [ 56%] (Sampling)
Chain 2 Iteration: 1300 / 2500 [ 52%] (Sampling)
Chain 2 Iteration: 1400 / 2500 [ 56%] (Sampling)
Chain 3 Iteration: 1300 / 2500 [ 52%] (Sampling)
Chain 3 Iteration: 1400 / 2500 [ 56%] (Sampling)
Chain 4 Iteration: 1200 / 2500 [ 48%] (Sampling)
Chain 4 Iteration: 1300 / 2500 [ 52%] (Sampling)
Chain 1 Iteration: 1500 / 2500 [ 60%] (Sampling)
Chain 1 Iteration: 1600 / 2500 [ 64%] (Sampling)
Chain 2 Iteration: 1500 / 2500 [ 60%] (Sampling)
Chain 2 Iteration: 1600 / 2500 [ 64%] (Sampling)
Chain 2 Iteration: 1700 / 2500 [ 68%] (Sampling)
Chain 3 Iteration: 1500 / 2500 [ 60%] (Sampling)
Chain 3 Iteration: 1600 / 2500 [ 64%] (Sampling)
Chain 4 Iteration: 1400 / 2500 [ 56%] (Sampling)
Chain 4 Iteration: 1500 / 2500 [ 60%] (Sampling)
Chain 4 Iteration: 1600 / 2500 [ 64%] (Sampling)
Chain 1 Iteration: 1700 / 2500 [ 68%] (Sampling)
Chain 1 Iteration: 1800 / 2500 [ 72%] (Sampling)
Chain 2 Iteration: 1800 / 2500 [ 72%] (Sampling)
Chain 2 Iteration: 1900 / 2500 [ 76%] (Sampling)
Chain 3 Iteration: 1700 / 2500 [ 68%] (Sampling)
Chain 3 Iteration: 1800 / 2500 [ 72%] (Sampling)
Chain 4 Iteration: 1700 / 2500 [ 68%] (Sampling)
Chain 4 Iteration: 1800 / 2500 [ 72%] (Sampling)
Chain 1 Iteration: 1900 / 2500 [ 76%] (Sampling)
Chain 1 Iteration: 2000 / 2500 [ 80%] (Sampling)
Chain 2 Iteration: 2000 / 2500 [ 80%] (Sampling)
Chain 2 Iteration: 2100 / 2500 [ 84%] (Sampling)
Chain 3 Iteration: 1900 / 2500 [ 76%] (Sampling)
Chain 3 Iteration: 2000 / 2500 [ 80%] (Sampling)
Chain 4 Iteration: 1900 / 2500 [ 76%] (Sampling)
Chain 4 Iteration: 2000 / 2500 [ 80%] (Sampling)
Chain 1 Iteration: 2100 / 2500 [ 84%] (Sampling)
Chain 1 Iteration: 2200 / 2500 [ 88%] (Sampling)
Chain 2 Iteration: 2200 / 2500 [ 88%] (Sampling)
Chain 2 Iteration: 2300 / 2500 [ 92%] (Sampling)
Chain 2 Iteration: 2400 / 2500 [ 96%] (Sampling)
Chain 3 Iteration: 2100 / 2500 [ 84%] (Sampling)
Chain 3 Iteration: 2200 / 2500 [ 88%] (Sampling)
Chain 3 Iteration: 2300 / 2500 [ 92%] (Sampling)
Chain 4 Iteration: 2100 / 2500 [ 84%] (Sampling)
Chain 4 Iteration: 2200 / 2500 [ 88%] (Sampling)
Chain 1 Iteration: 2300 / 2500 [ 92%] (Sampling)
Chain 1 Iteration: 2400 / 2500 [ 96%] (Sampling)
Chain 2 Iteration: 2500 / 2500 [100%] (Sampling)
Chain 3 Iteration: 2400 / 2500 [ 96%] (Sampling)
Chain 3 Iteration: 2500 / 2500 [100%] (Sampling)
Chain 4 Iteration: 2300 / 2500 [ 92%] (Sampling)
Chain 4 Iteration: 2400 / 2500 [ 96%] (Sampling)
Chain 2 finished in 1.1 seconds.
Chain 3 finished in 1.1 seconds.
Chain 4 Iteration: 2500 / 2500 [100%] (Sampling)
Chain 4 finished in 1.2 seconds.
Chain 1 Iteration: 2500 / 2500 [100%] (Sampling)
Chain 1 finished in 1.2 seconds.
All 4 chains finished successfully.
Mean chain execution time: 1.2 seconds.
Total execution time: 1.3 seconds.rethinking::precis(m_12h4) mean sd 5.5% 94.5% rhat ess_bulk
a 2.32495080 0.1180601 2.1408057 2.5139438 1.001215 6397.718
bd 1.23537431 0.1469832 1.0006462 1.4728088 1.000433 5389.289
bp -0.09087182 0.1195969 -0.2826927 0.1009129 1.000536 5587.925
phi 1.00910491 0.1677158 0.7612470 1.2930954 1.001479 6317.246Now let’s compare the two models.
rethinking::compare(m_12h3_b, m_12h4, sort = "PSIS", func = PSIS) PSIS SE dPSIS dSE pPSIS weight
m_12h4 633.9923 32.92681 0.0000 NA 5.832550 1.000000e+00
m_12h3_b 670.7927 38.26946 36.8004 13.48972 7.875416 1.020691e-08The two models are similar, but it looks like the log model is narrowly better than the model with damage_norm on the natural scale. The PSIS criteria are more than one standard error different, but less than two standard errors different, so it’s probably worth using the log scale predictor instead but it doesn’t seem to make a HUGE difference. We should also notice that the Pareto \(k\) values are, in general, a little bit better for the log-scale predictor model. Now let’s look at the implied predictions.
mp_seq <- c(900, 925, 950, 975, 1000)
mp_seq_std <- (mp_seq - attr(dh2$mp, "scaled:center")) /
attr(dh2$mp, "scaled:scale")
cols <- blues9[c(5, 6, 7, 8, 9)]
dn_seq_nat <- seq(1, 75001, 2500)
dn_seq_nat_std <- (dn_seq_nat - attr(dh2$dn, "scaled:center")) /
attr(dh2$dn, "scaled:scale")
pred_data_nat <- expand.grid(
mp = mp_seq_std,
dn = dn_seq_nat_std
)
m_12h3_b_sim <- rethinking::link(m_12h3_b, data = pred_data_nat)
m_12h3_b_mean <- colMeans(m_12h3_b_sim)
m_12h3_b_pi <- apply(m_12h3_b_sim, 2, rethinking::PI)
dn_seq_log <- seq(0, 11.5, 0.5)
dn_seq_log_std <- (dn_seq_log - attr(dh2$log_dn, "scaled:center")) /
attr(dh2$log_dn, "scaled:scale")
pred_data_log <- expand.grid(
mp = mp_seq_std,
log_dn = dn_seq_log_std
)
m_12h4_sim <- rethinking::link(m_12h4, data = pred_data_log)
m_12h4_mean <- colMeans(m_12h4_sim)
m_12h4_pi <- apply(m_12h4_sim, 2, rethinking::PI)
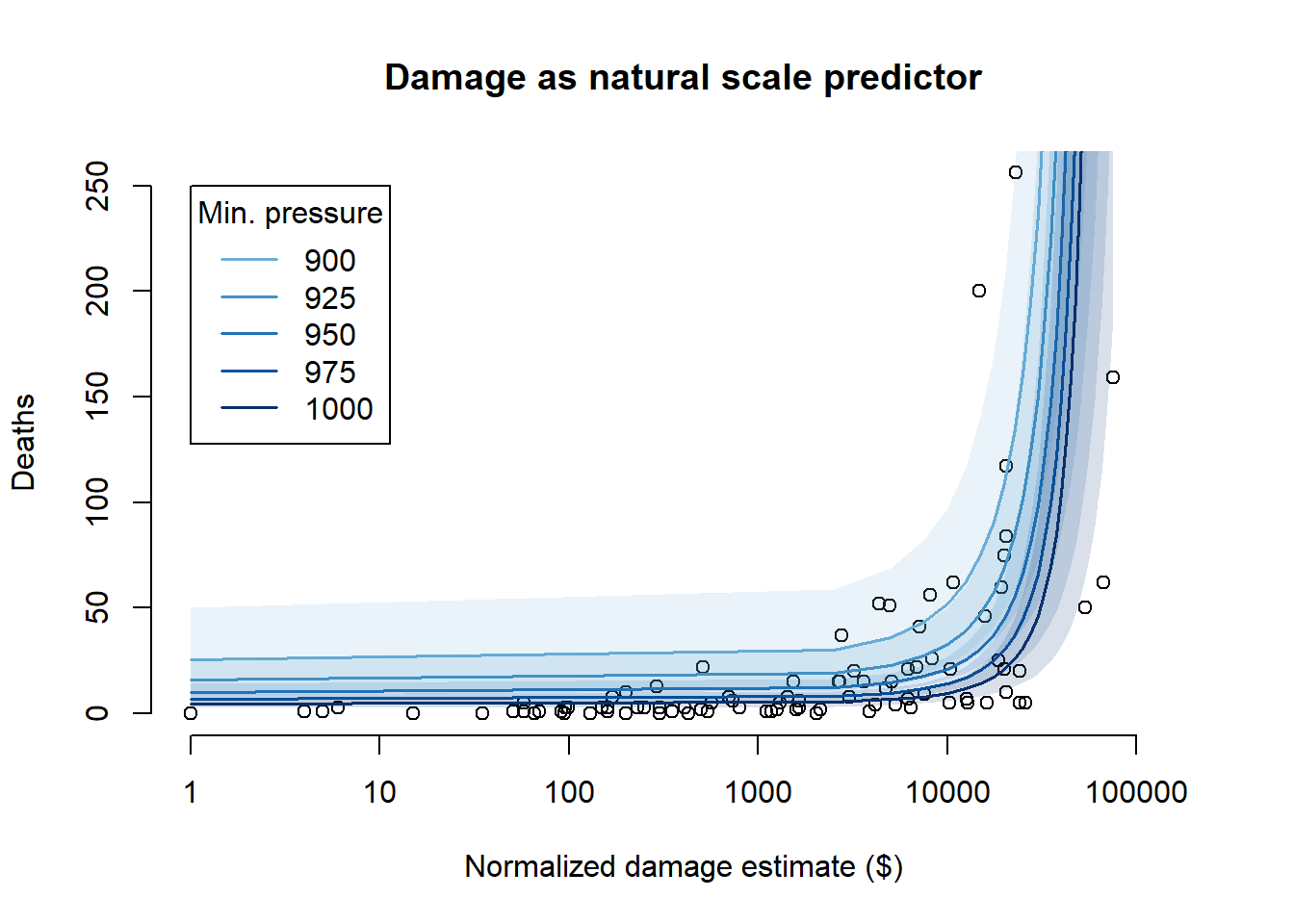
# Natural scale predictor plot
plot(
log(Hurricanes$damage_norm),
Hurricanes$deaths,
xlab = "Normalized damage estimate ($)",
ylab = "Deaths",
axes = FALSE,
xlim = c(0, 12),
ylim = range(Hurricanes$deaths),
main = "Damage as natural scale predictor"
)
axis(
1,
at = log(c(1, 10, 100, 1000, 10000, 100000)),
labels = c(1, 10, 100, 1000, 10000, "100000")
)
axis(2, at = seq(0, 250, 50))
for (i in 1:length(mp_seq)) {
plot_ind <- which(pred_data_nat$mp == mp_seq_std[i])
plot_x <- pred_data_nat$dn[plot_ind] * attr(dh2$dn, "scaled:scale") +
attr(dh2$dn, "scaled:center")
rethinking::shade(
m_12h3_b_pi[,plot_ind], log(plot_x),
col = rethinking::col.alpha(cols[i], alpha = 0.15)
)
lines(log(plot_x), m_12h3_b_mean[plot_ind], col = cols[i], lwd = 1.5)
}
legend(
x = 0,
y = 250,
col = cols,
lty = 1,
lwd = 1.5,
title = "Min. pressure",
legend = mp_seq
)
# Log scale predictor plot
plot(
log(Hurricanes$damage_norm),
Hurricanes$deaths,
xlab = "Normalized damage estimate ($)",
ylab = "Deaths",
axes = FALSE,
xlim = c(0, 12),
ylim = range(Hurricanes$deaths),
main = "Damage as log scale predictor"
)
axis(
1,
at = log(c(1, 10, 100, 1000, 10000, 100000)),
labels = c(1, 10, 100, 1000, 10000, "100000")
)
axis(2, at = seq(0, 250, 50))
for (i in 1:length(mp_seq)) {
plot_ind <- which(pred_data_log$mp == mp_seq_std[i])
plot_x <- pred_data_log$log_dn[plot_ind] * attr(dh2$log_dn, "scaled:scale") +
attr(dh2$log_dn, "scaled:center")
rethinking::shade(
m_12h4_pi[,plot_ind], plot_x,
col = rethinking::col.alpha(cols[i], alpha = 0.15)
)
lines(plot_x, m_12h4_mean[plot_ind], col = cols[i], lwd = 1.5)
}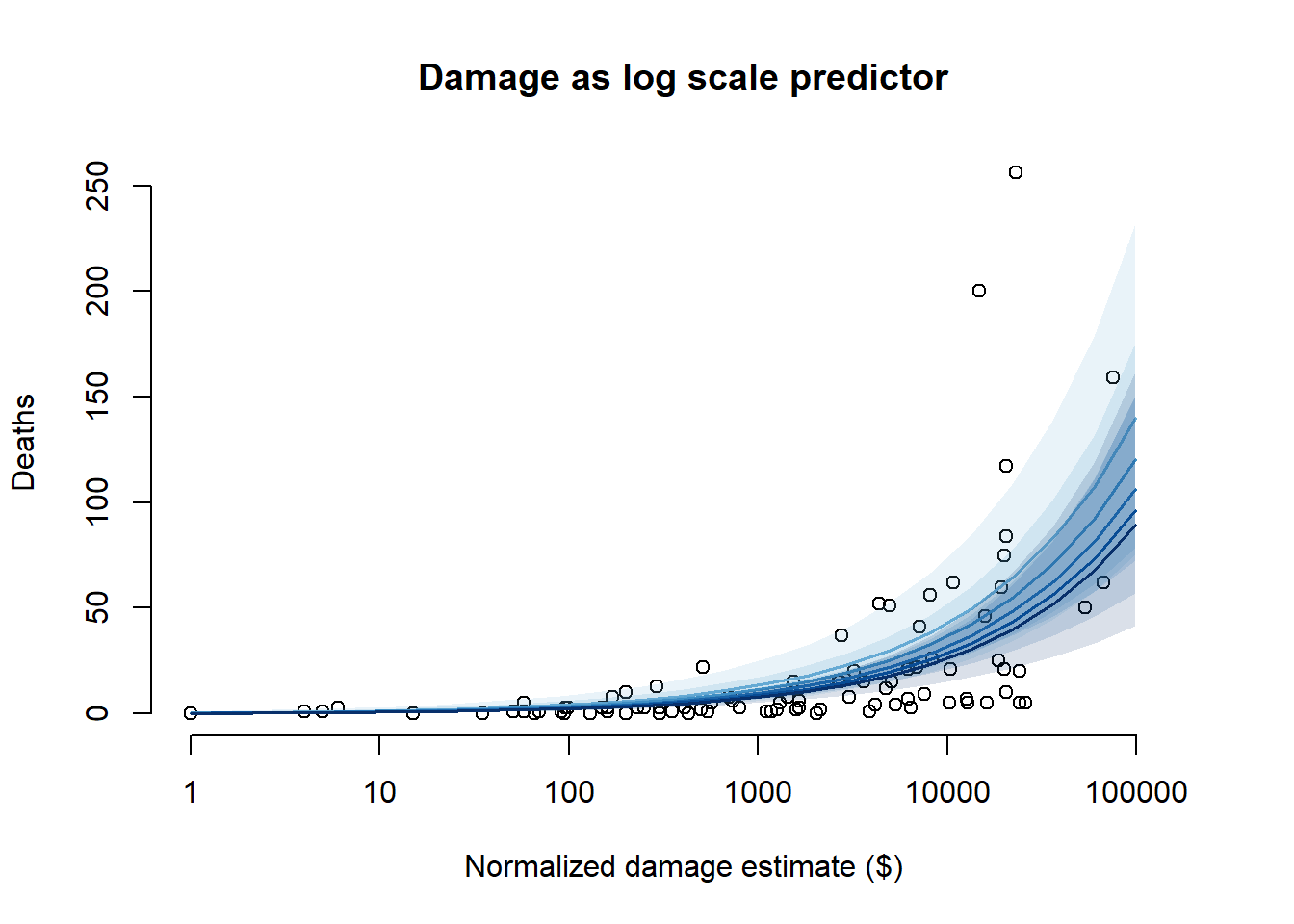
From the predictions, we can see that using normalized damage estimate as a log scale predictor is, in general, more sensible – while the natural scale predictor has a sharp upward asymptote which allows it to get closer to some of the more extreme points, it predicts many deaths that are orders of magnitude above what we observed in the actual data. The log-scale predictor products more reasonable predictions, even at high levels of damage. The log-scale predictor also doesn’t lead to unnatural predictions when we consider the minimum pressure at the same time – it allows for a low number of deaths regardless of what the pressure is, whereas the natural scale predictor forces a high number of deaths at low minimum pressures even when the damage is small.
So, overall, we should prefer the log-scale predictor.
12H5
Now we’ll go to the trolley data.
data("Trolley", package = "rethinking")
dt <- list(
G = Trolley$male,
A = Trolley$action,
C = Trolley$contact,
I = Trolley$intention,
R = Trolley$response
)We’ll build the same model that we ended up choosing to describe the interaction between intention and other variables in the chapter. But we’ll also build three models with gender: one where gender only affects the intercept, one where the effect of contact changes with gender, and one that has an addition three-way gender/contact/interaction term.
First, the model m12.5 from the chapter. This model took about 25 minutes (1484.1 seconds) to run for me with these settings.
m_12h5_a <- rethinking::ulam(
alist(
R ~ dordlogit(phi, cutpoints),
phi <- bA * A + bC * C + BI * I,
BI <- bI + bIA * A + bIC * C,
c(bA, bI, bC, bIA, bIC) ~ dnorm(0, 0.5),
cutpoints ~ dnorm(0, 1.5)
),
data = dt,
chains = 4, cores = 4,
iter = 2500, warmup = 500,
log_lik = TRUE
)Running MCMC with 4 parallel chains, with 1 thread(s) per chain...Chain 1 Iteration: 1 / 2500 [ 0%] (Warmup) Chain 2 Iteration: 1 / 2500 [ 0%] (Warmup) Chain 3 Iteration: 1 / 2500 [ 0%] (Warmup) Chain 4 Iteration: 1 / 2500 [ 0%] (Warmup) Chain 2 Iteration: 100 / 2500 [ 4%] (Warmup)
Chain 3 Iteration: 100 / 2500 [ 4%] (Warmup)
Chain 4 Iteration: 100 / 2500 [ 4%] (Warmup)
Chain 1 Iteration: 100 / 2500 [ 4%] (Warmup)
Chain 2 Iteration: 200 / 2500 [ 8%] (Warmup)
Chain 4 Iteration: 200 / 2500 [ 8%] (Warmup)
Chain 3 Iteration: 200 / 2500 [ 8%] (Warmup)
Chain 1 Iteration: 200 / 2500 [ 8%] (Warmup)
Chain 4 Iteration: 300 / 2500 [ 12%] (Warmup)
Chain 2 Iteration: 300 / 2500 [ 12%] (Warmup)
Chain 3 Iteration: 300 / 2500 [ 12%] (Warmup)
Chain 1 Iteration: 300 / 2500 [ 12%] (Warmup)
Chain 4 Iteration: 400 / 2500 [ 16%] (Warmup)
Chain 2 Iteration: 400 / 2500 [ 16%] (Warmup)
Chain 3 Iteration: 400 / 2500 [ 16%] (Warmup)
Chain 1 Iteration: 400 / 2500 [ 16%] (Warmup)
Chain 4 Iteration: 500 / 2500 [ 20%] (Warmup)
Chain 4 Iteration: 501 / 2500 [ 20%] (Sampling)
Chain 2 Iteration: 500 / 2500 [ 20%] (Warmup)
Chain 2 Iteration: 501 / 2500 [ 20%] (Sampling)
Chain 3 Iteration: 500 / 2500 [ 20%] (Warmup)
Chain 3 Iteration: 501 / 2500 [ 20%] (Sampling)
Chain 1 Iteration: 500 / 2500 [ 20%] (Warmup)
Chain 1 Iteration: 501 / 2500 [ 20%] (Sampling)
Chain 4 Iteration: 600 / 2500 [ 24%] (Sampling)
Chain 3 Iteration: 600 / 2500 [ 24%] (Sampling)
Chain 2 Iteration: 600 / 2500 [ 24%] (Sampling)
Chain 4 Iteration: 700 / 2500 [ 28%] (Sampling)
Chain 1 Iteration: 600 / 2500 [ 24%] (Sampling)
Chain 3 Iteration: 700 / 2500 [ 28%] (Sampling)
Chain 2 Iteration: 700 / 2500 [ 28%] (Sampling)
Chain 4 Iteration: 800 / 2500 [ 32%] (Sampling)
Chain 1 Iteration: 700 / 2500 [ 28%] (Sampling)
Chain 3 Iteration: 800 / 2500 [ 32%] (Sampling)
Chain 4 Iteration: 900 / 2500 [ 36%] (Sampling)
Chain 2 Iteration: 800 / 2500 [ 32%] (Sampling)
Chain 3 Iteration: 900 / 2500 [ 36%] (Sampling)
Chain 1 Iteration: 800 / 2500 [ 32%] (Sampling)
Chain 4 Iteration: 1000 / 2500 [ 40%] (Sampling)
Chain 2 Iteration: 900 / 2500 [ 36%] (Sampling)
Chain 3 Iteration: 1000 / 2500 [ 40%] (Sampling)
Chain 1 Iteration: 900 / 2500 [ 36%] (Sampling)
Chain 4 Iteration: 1100 / 2500 [ 44%] (Sampling)
Chain 2 Iteration: 1000 / 2500 [ 40%] (Sampling)
Chain 3 Iteration: 1100 / 2500 [ 44%] (Sampling)
Chain 1 Iteration: 1000 / 2500 [ 40%] (Sampling)
Chain 4 Iteration: 1200 / 2500 [ 48%] (Sampling)
Chain 3 Iteration: 1200 / 2500 [ 48%] (Sampling)
Chain 2 Iteration: 1100 / 2500 [ 44%] (Sampling)
Chain 1 Iteration: 1100 / 2500 [ 44%] (Sampling)
Chain 4 Iteration: 1300 / 2500 [ 52%] (Sampling)
Chain 3 Iteration: 1300 / 2500 [ 52%] (Sampling)
Chain 2 Iteration: 1200 / 2500 [ 48%] (Sampling)
Chain 1 Iteration: 1200 / 2500 [ 48%] (Sampling)
Chain 4 Iteration: 1400 / 2500 [ 56%] (Sampling)
Chain 3 Iteration: 1400 / 2500 [ 56%] (Sampling)
Chain 2 Iteration: 1300 / 2500 [ 52%] (Sampling)
Chain 4 Iteration: 1500 / 2500 [ 60%] (Sampling)
Chain 1 Iteration: 1300 / 2500 [ 52%] (Sampling)
Chain 3 Iteration: 1500 / 2500 [ 60%] (Sampling)
Chain 2 Iteration: 1400 / 2500 [ 56%] (Sampling)
Chain 4 Iteration: 1600 / 2500 [ 64%] (Sampling)
Chain 3 Iteration: 1600 / 2500 [ 64%] (Sampling)
Chain 1 Iteration: 1400 / 2500 [ 56%] (Sampling)
Chain 4 Iteration: 1700 / 2500 [ 68%] (Sampling)
Chain 2 Iteration: 1500 / 2500 [ 60%] (Sampling)
Chain 3 Iteration: 1700 / 2500 [ 68%] (Sampling)
Chain 1 Iteration: 1500 / 2500 [ 60%] (Sampling)
Chain 4 Iteration: 1800 / 2500 [ 72%] (Sampling)
Chain 2 Iteration: 1600 / 2500 [ 64%] (Sampling)
Chain 3 Iteration: 1800 / 2500 [ 72%] (Sampling)
Chain 1 Iteration: 1600 / 2500 [ 64%] (Sampling)
Chain 4 Iteration: 1900 / 2500 [ 76%] (Sampling)
Chain 3 Iteration: 1900 / 2500 [ 76%] (Sampling)
Chain 2 Iteration: 1700 / 2500 [ 68%] (Sampling)
Chain 1 Iteration: 1700 / 2500 [ 68%] (Sampling)
Chain 4 Iteration: 2000 / 2500 [ 80%] (Sampling)
Chain 3 Iteration: 2000 / 2500 [ 80%] (Sampling)
Chain 2 Iteration: 1800 / 2500 [ 72%] (Sampling)
Chain 1 Iteration: 1800 / 2500 [ 72%] (Sampling)
Chain 4 Iteration: 2100 / 2500 [ 84%] (Sampling)
Chain 3 Iteration: 2100 / 2500 [ 84%] (Sampling)
Chain 2 Iteration: 1900 / 2500 [ 76%] (Sampling)
Chain 4 Iteration: 2200 / 2500 [ 88%] (Sampling)
Chain 1 Iteration: 1900 / 2500 [ 76%] (Sampling)
Chain 3 Iteration: 2200 / 2500 [ 88%] (Sampling)
Chain 4 Iteration: 2300 / 2500 [ 92%] (Sampling)
Chain 2 Iteration: 2000 / 2500 [ 80%] (Sampling)
Chain 3 Iteration: 2300 / 2500 [ 92%] (Sampling)
Chain 1 Iteration: 2000 / 2500 [ 80%] (Sampling)
Chain 4 Iteration: 2400 / 2500 [ 96%] (Sampling)
Chain 3 Iteration: 2400 / 2500 [ 96%] (Sampling)
Chain 2 Iteration: 2100 / 2500 [ 84%] (Sampling)
Chain 1 Iteration: 2100 / 2500 [ 84%] (Sampling)
Chain 4 Iteration: 2500 / 2500 [100%] (Sampling)
Chain 4 finished in 1391.3 seconds.
Chain 3 Iteration: 2500 / 2500 [100%] (Sampling)
Chain 3 finished in 1393.6 seconds.
Chain 2 Iteration: 2200 / 2500 [ 88%] (Sampling)
Chain 1 Iteration: 2200 / 2500 [ 88%] (Sampling)
Chain 2 Iteration: 2300 / 2500 [ 92%] (Sampling)
Chain 1 Iteration: 2300 / 2500 [ 92%] (Sampling)
Chain 1 Iteration: 2400 / 2500 [ 96%] (Sampling)
Chain 2 Iteration: 2400 / 2500 [ 96%] (Sampling)
Chain 1 Iteration: 2500 / 2500 [100%] (Sampling)
Chain 1 finished in 1597.8 seconds.
Chain 2 Iteration: 2500 / 2500 [100%] (Sampling)
Chain 2 finished in 1605.1 seconds.
All 4 chains finished successfully.
Mean chain execution time: 1496.9 seconds.
Total execution time: 1605.5 seconds.rethinking::precis(m_12h5_a, depth = 2) mean sd 5.5% 94.5% rhat ess_bulk
bIC -1.2371744 0.09577277 -1.3905310 -1.0847845 0.9999799 4593.568
bIA -0.4335846 0.07807587 -0.5579324 -0.3101173 1.0005097 3964.343
bC -0.3417313 0.06759136 -0.4489125 -0.2330469 0.9999201 4596.914
bI -0.2914020 0.05629041 -0.3793786 -0.2025822 1.0007796 3680.158
bA -0.4724483 0.05351378 -0.5568422 -0.3869026 1.0004098 3965.008
cutpoints[1] -2.6324271 0.05161376 -2.7158122 -2.5491252 1.0005970 4103.601
cutpoints[2] -1.9373031 0.04762585 -2.0127506 -1.8605889 1.0007632 4156.629
cutpoints[3] -1.3425596 0.04529764 -1.4143906 -1.2697384 1.0008531 4090.881
cutpoints[4] -0.3085618 0.04311912 -0.3775730 -0.2404055 1.0004977 3991.593
cutpoints[5] 0.3621618 0.04325963 0.2940322 0.4317230 1.0007230 4157.959
cutpoints[6] 1.2681533 0.04559868 1.1954984 1.3405927 1.0000830 4498.046Next a model with an effect of gender (coded as an indicator variable for being male). This one also took about 25 minutes (1615.9 seconds).
m_12h5_b <- rethinking::ulam(
alist(
R ~ dordlogit(phi, cutpoints),
phi <- bG * G + bA * A + bC * C + BI * I,
BI <- bI + bIA * A + bIC * C,
c(bG, bA, bI, bC, bIA, bIC) ~ dnorm(0, 0.5),
cutpoints ~ dnorm(0, 1.5)
),
data = dt,
chains = 4, cores = 4,
iter = 2500, warmup = 500,
log_lik = TRUE
)Running MCMC with 4 parallel chains, with 1 thread(s) per chain...Chain 1 Iteration: 1 / 2500 [ 0%] (Warmup) Chain 2 Iteration: 1 / 2500 [ 0%] (Warmup) Chain 3 Iteration: 1 / 2500 [ 0%] (Warmup) Chain 4 Iteration: 1 / 2500 [ 0%] (Warmup) Chain 3 Iteration: 100 / 2500 [ 4%] (Warmup)
Chain 4 Iteration: 100 / 2500 [ 4%] (Warmup)
Chain 2 Iteration: 100 / 2500 [ 4%] (Warmup)
Chain 1 Iteration: 100 / 2500 [ 4%] (Warmup)
Chain 4 Iteration: 200 / 2500 [ 8%] (Warmup)
Chain 3 Iteration: 200 / 2500 [ 8%] (Warmup)
Chain 2 Iteration: 200 / 2500 [ 8%] (Warmup)
Chain 1 Iteration: 200 / 2500 [ 8%] (Warmup)
Chain 4 Iteration: 300 / 2500 [ 12%] (Warmup)
Chain 3 Iteration: 300 / 2500 [ 12%] (Warmup)
Chain 2 Iteration: 300 / 2500 [ 12%] (Warmup)
Chain 1 Iteration: 300 / 2500 [ 12%] (Warmup)
Chain 4 Iteration: 400 / 2500 [ 16%] (Warmup)
Chain 3 Iteration: 400 / 2500 [ 16%] (Warmup)
Chain 2 Iteration: 400 / 2500 [ 16%] (Warmup)
Chain 1 Iteration: 400 / 2500 [ 16%] (Warmup)
Chain 3 Iteration: 500 / 2500 [ 20%] (Warmup)
Chain 3 Iteration: 501 / 2500 [ 20%] (Sampling)
Chain 4 Iteration: 500 / 2500 [ 20%] (Warmup)
Chain 4 Iteration: 501 / 2500 [ 20%] (Sampling)
Chain 2 Iteration: 500 / 2500 [ 20%] (Warmup)
Chain 2 Iteration: 501 / 2500 [ 20%] (Sampling)
Chain 1 Iteration: 500 / 2500 [ 20%] (Warmup)
Chain 1 Iteration: 501 / 2500 [ 20%] (Sampling)
Chain 4 Iteration: 600 / 2500 [ 24%] (Sampling)
Chain 3 Iteration: 600 / 2500 [ 24%] (Sampling)
Chain 2 Iteration: 600 / 2500 [ 24%] (Sampling)
Chain 4 Iteration: 700 / 2500 [ 28%] (Sampling)
Chain 1 Iteration: 600 / 2500 [ 24%] (Sampling)
Chain 3 Iteration: 700 / 2500 [ 28%] (Sampling)
Chain 2 Iteration: 700 / 2500 [ 28%] (Sampling)
Chain 4 Iteration: 800 / 2500 [ 32%] (Sampling)
Chain 3 Iteration: 800 / 2500 [ 32%] (Sampling)
Chain 1 Iteration: 700 / 2500 [ 28%] (Sampling)
Chain 2 Iteration: 800 / 2500 [ 32%] (Sampling)
Chain 4 Iteration: 900 / 2500 [ 36%] (Sampling)
Chain 2 Iteration: 900 / 2500 [ 36%] (Sampling)
Chain 3 Iteration: 900 / 2500 [ 36%] (Sampling)
Chain 1 Iteration: 800 / 2500 [ 32%] (Sampling)
Chain 4 Iteration: 1000 / 2500 [ 40%] (Sampling)
Chain 3 Iteration: 1000 / 2500 [ 40%] (Sampling)
Chain 2 Iteration: 1000 / 2500 [ 40%] (Sampling)
Chain 1 Iteration: 900 / 2500 [ 36%] (Sampling)
Chain 4 Iteration: 1100 / 2500 [ 44%] (Sampling)
Chain 2 Iteration: 1100 / 2500 [ 44%] (Sampling)
Chain 3 Iteration: 1100 / 2500 [ 44%] (Sampling)
Chain 1 Iteration: 1000 / 2500 [ 40%] (Sampling)
Chain 4 Iteration: 1200 / 2500 [ 48%] (Sampling)
Chain 2 Iteration: 1200 / 2500 [ 48%] (Sampling)
Chain 3 Iteration: 1200 / 2500 [ 48%] (Sampling)
Chain 1 Iteration: 1100 / 2500 [ 44%] (Sampling)
Chain 4 Iteration: 1300 / 2500 [ 52%] (Sampling)
Chain 2 Iteration: 1300 / 2500 [ 52%] (Sampling)
Chain 3 Iteration: 1300 / 2500 [ 52%] (Sampling)
Chain 1 Iteration: 1200 / 2500 [ 48%] (Sampling)
Chain 4 Iteration: 1400 / 2500 [ 56%] (Sampling)
Chain 2 Iteration: 1400 / 2500 [ 56%] (Sampling)
Chain 3 Iteration: 1400 / 2500 [ 56%] (Sampling)
Chain 1 Iteration: 1300 / 2500 [ 52%] (Sampling)
Chain 4 Iteration: 1500 / 2500 [ 60%] (Sampling)
Chain 2 Iteration: 1500 / 2500 [ 60%] (Sampling)
Chain 3 Iteration: 1500 / 2500 [ 60%] (Sampling)
Chain 4 Iteration: 1600 / 2500 [ 64%] (Sampling)
Chain 1 Iteration: 1400 / 2500 [ 56%] (Sampling)
Chain 2 Iteration: 1600 / 2500 [ 64%] (Sampling)
Chain 3 Iteration: 1600 / 2500 [ 64%] (Sampling)
Chain 4 Iteration: 1700 / 2500 [ 68%] (Sampling)
Chain 2 Iteration: 1700 / 2500 [ 68%] (Sampling)
Chain 1 Iteration: 1500 / 2500 [ 60%] (Sampling)
Chain 3 Iteration: 1700 / 2500 [ 68%] (Sampling)
Chain 4 Iteration: 1800 / 2500 [ 72%] (Sampling)
Chain 2 Iteration: 1800 / 2500 [ 72%] (Sampling)
Chain 1 Iteration: 1600 / 2500 [ 64%] (Sampling)
Chain 3 Iteration: 1800 / 2500 [ 72%] (Sampling)
Chain 4 Iteration: 1900 / 2500 [ 76%] (Sampling)
Chain 2 Iteration: 1900 / 2500 [ 76%] (Sampling)
Chain 3 Iteration: 1900 / 2500 [ 76%] (Sampling)
Chain 1 Iteration: 1700 / 2500 [ 68%] (Sampling)
Chain 4 Iteration: 2000 / 2500 [ 80%] (Sampling)
Chain 2 Iteration: 2000 / 2500 [ 80%] (Sampling)
Chain 3 Iteration: 2000 / 2500 [ 80%] (Sampling)
Chain 1 Iteration: 1800 / 2500 [ 72%] (Sampling)
Chain 4 Iteration: 2100 / 2500 [ 84%] (Sampling)
Chain 2 Iteration: 2100 / 2500 [ 84%] (Sampling)
Chain 3 Iteration: 2100 / 2500 [ 84%] (Sampling)
Chain 1 Iteration: 1900 / 2500 [ 76%] (Sampling)
Chain 2 Iteration: 2200 / 2500 [ 88%] (Sampling)
Chain 4 Iteration: 2200 / 2500 [ 88%] (Sampling)
Chain 3 Iteration: 2200 / 2500 [ 88%] (Sampling)
Chain 1 Iteration: 2000 / 2500 [ 80%] (Sampling)
Chain 2 Iteration: 2300 / 2500 [ 92%] (Sampling)
Chain 4 Iteration: 2300 / 2500 [ 92%] (Sampling)
Chain 3 Iteration: 2300 / 2500 [ 92%] (Sampling)
Chain 2 Iteration: 2400 / 2500 [ 96%] (Sampling)
Chain 4 Iteration: 2400 / 2500 [ 96%] (Sampling)
Chain 1 Iteration: 2100 / 2500 [ 84%] (Sampling)
Chain 3 Iteration: 2400 / 2500 [ 96%] (Sampling)
Chain 2 Iteration: 2500 / 2500 [100%] (Sampling)
Chain 2 finished in 1442.5 seconds.
Chain 4 Iteration: 2500 / 2500 [100%] (Sampling)
Chain 4 finished in 1454.2 seconds.
Chain 1 Iteration: 2200 / 2500 [ 88%] (Sampling)
Chain 3 Iteration: 2500 / 2500 [100%] (Sampling)
Chain 3 finished in 1482.3 seconds.
Chain 1 Iteration: 2300 / 2500 [ 92%] (Sampling)
Chain 1 Iteration: 2400 / 2500 [ 96%] (Sampling)
Chain 1 Iteration: 2500 / 2500 [100%] (Sampling)
Chain 1 finished in 1623.0 seconds.
All 4 chains finished successfully.
Mean chain execution time: 1500.5 seconds.
Total execution time: 1623.5 seconds.rethinking::precis(m_12h5_b, depth = 2) mean sd 5.5% 94.5% rhat ess_bulk
bIC -1.25866146 0.09798056 -1.41554110 -1.10175945 1.0002112 5005.749
bIA -0.43897106 0.07992380 -0.56646832 -0.31096101 1.0007073 4677.893
bC -0.34503263 0.06800850 -0.45206355 -0.23581296 1.0004127 5292.388
bI -0.29387469 0.05731325 -0.38642423 -0.20378604 1.0003001 4240.205
bA -0.47674114 0.05417614 -0.56374768 -0.39171282 1.0006680 4219.182
bG 0.57252584 0.03622578 0.51436958 0.63058704 0.9998745 8812.485
cutpoints[1] -2.35597132 0.05392522 -2.44229165 -2.26835900 1.0005290 4254.036
cutpoints[2] -1.66031384 0.05017707 -1.74088110 -1.58009725 1.0006854 4430.472
cutpoints[3] -1.05917170 0.04850332 -1.13725275 -0.98117907 1.0006825 4511.116
cutpoints[4] -0.00209887 0.04740780 -0.07710696 0.07331166 1.0006824 4384.914
cutpoints[5] 0.68705398 0.04802786 0.61066397 0.76367646 1.0005248 4498.392
cutpoints[6] 1.61296077 0.05098202 1.53212945 1.69488770 1.0006168 4765.787Next a model with an effect of gender and an interaction between gender and contact. This one took a bit less than 30 minutes (1718.5 seconds).
m_12h5_c <- rethinking::ulam(
alist(
R ~ dordlogit(phi, cutpoints),
phi <- bG * G + bA * A + BC * C + BI * I,
BC <- bC + bCG * G,
BI <- bI + bIA * A + bIC * C,
c(bG, bA, bI, bC, bIA, bIC, bCG) ~ dnorm(0, 0.5),
cutpoints ~ dnorm(0, 1.5)
),
data = dt,
chains = 4, cores = 4,
iter = 2500, warmup = 500,
log_lik = TRUE
)Running MCMC with 4 parallel chains, with 1 thread(s) per chain...Chain 1 Iteration: 1 / 2500 [ 0%] (Warmup) Chain 2 Iteration: 1 / 2500 [ 0%] (Warmup) Chain 3 Iteration: 1 / 2500 [ 0%] (Warmup) Chain 4 Iteration: 1 / 2500 [ 0%] (Warmup) Chain 2 Iteration: 100 / 2500 [ 4%] (Warmup)
Chain 3 Iteration: 100 / 2500 [ 4%] (Warmup)
Chain 4 Iteration: 100 / 2500 [ 4%] (Warmup)
Chain 1 Iteration: 100 / 2500 [ 4%] (Warmup)
Chain 1 Iteration: 200 / 2500 [ 8%] (Warmup)
Chain 4 Iteration: 200 / 2500 [ 8%] (Warmup)
Chain 3 Iteration: 200 / 2500 [ 8%] (Warmup)
Chain 2 Iteration: 200 / 2500 [ 8%] (Warmup)
Chain 1 Iteration: 300 / 2500 [ 12%] (Warmup)
Chain 4 Iteration: 300 / 2500 [ 12%] (Warmup)
Chain 2 Iteration: 300 / 2500 [ 12%] (Warmup)
Chain 3 Iteration: 300 / 2500 [ 12%] (Warmup)
Chain 1 Iteration: 400 / 2500 [ 16%] (Warmup)
Chain 4 Iteration: 400 / 2500 [ 16%] (Warmup)
Chain 3 Iteration: 400 / 2500 [ 16%] (Warmup)
Chain 2 Iteration: 400 / 2500 [ 16%] (Warmup)
Chain 1 Iteration: 500 / 2500 [ 20%] (Warmup)
Chain 1 Iteration: 501 / 2500 [ 20%] (Sampling)
Chain 3 Iteration: 500 / 2500 [ 20%] (Warmup)
Chain 3 Iteration: 501 / 2500 [ 20%] (Sampling)
Chain 4 Iteration: 500 / 2500 [ 20%] (Warmup)
Chain 4 Iteration: 501 / 2500 [ 20%] (Sampling)
Chain 2 Iteration: 500 / 2500 [ 20%] (Warmup)
Chain 2 Iteration: 501 / 2500 [ 20%] (Sampling)
Chain 1 Iteration: 600 / 2500 [ 24%] (Sampling)
Chain 3 Iteration: 600 / 2500 [ 24%] (Sampling)
Chain 2 Iteration: 600 / 2500 [ 24%] (Sampling)
Chain 4 Iteration: 600 / 2500 [ 24%] (Sampling)
Chain 1 Iteration: 700 / 2500 [ 28%] (Sampling)
Chain 3 Iteration: 700 / 2500 [ 28%] (Sampling)
Chain 2 Iteration: 700 / 2500 [ 28%] (Sampling)
Chain 4 Iteration: 700 / 2500 [ 28%] (Sampling)
Chain 3 Iteration: 800 / 2500 [ 32%] (Sampling)
Chain 1 Iteration: 800 / 2500 [ 32%] (Sampling)
Chain 2 Iteration: 800 / 2500 [ 32%] (Sampling)
Chain 3 Iteration: 900 / 2500 [ 36%] (Sampling)
Chain 4 Iteration: 800 / 2500 [ 32%] (Sampling)
Chain 2 Iteration: 900 / 2500 [ 36%] (Sampling)
Chain 1 Iteration: 900 / 2500 [ 36%] (Sampling)
Chain 3 Iteration: 1000 / 2500 [ 40%] (Sampling)
Chain 4 Iteration: 900 / 2500 [ 36%] (Sampling)
Chain 2 Iteration: 1000 / 2500 [ 40%] (Sampling)
Chain 1 Iteration: 1000 / 2500 [ 40%] (Sampling)
Chain 3 Iteration: 1100 / 2500 [ 44%] (Sampling)
Chain 2 Iteration: 1100 / 2500 [ 44%] (Sampling)
Chain 4 Iteration: 1000 / 2500 [ 40%] (Sampling)
Chain 3 Iteration: 1200 / 2500 [ 48%] (Sampling)
Chain 1 Iteration: 1100 / 2500 [ 44%] (Sampling)
Chain 2 Iteration: 1200 / 2500 [ 48%] (Sampling)
Chain 4 Iteration: 1100 / 2500 [ 44%] (Sampling)
Chain 3 Iteration: 1300 / 2500 [ 52%] (Sampling)
Chain 1 Iteration: 1200 / 2500 [ 48%] (Sampling)
Chain 2 Iteration: 1300 / 2500 [ 52%] (Sampling)
Chain 3 Iteration: 1400 / 2500 [ 56%] (Sampling)
Chain 4 Iteration: 1200 / 2500 [ 48%] (Sampling)
Chain 2 Iteration: 1400 / 2500 [ 56%] (Sampling)
Chain 1 Iteration: 1300 / 2500 [ 52%] (Sampling)
Chain 3 Iteration: 1500 / 2500 [ 60%] (Sampling)
Chain 4 Iteration: 1300 / 2500 [ 52%] (Sampling)
Chain 2 Iteration: 1500 / 2500 [ 60%] (Sampling)
Chain 3 Iteration: 1600 / 2500 [ 64%] (Sampling)
Chain 1 Iteration: 1400 / 2500 [ 56%] (Sampling)
Chain 2 Iteration: 1600 / 2500 [ 64%] (Sampling)
Chain 4 Iteration: 1400 / 2500 [ 56%] (Sampling)
Chain 3 Iteration: 1700 / 2500 [ 68%] (Sampling)
Chain 1 Iteration: 1500 / 2500 [ 60%] (Sampling)
Chain 2 Iteration: 1700 / 2500 [ 68%] (Sampling)
Chain 4 Iteration: 1500 / 2500 [ 60%] (Sampling)
Chain 3 Iteration: 1800 / 2500 [ 72%] (Sampling)
Chain 2 Iteration: 1800 / 2500 [ 72%] (Sampling)
Chain 1 Iteration: 1600 / 2500 [ 64%] (Sampling)
Chain 3 Iteration: 1900 / 2500 [ 76%] (Sampling)
Chain 4 Iteration: 1600 / 2500 [ 64%] (Sampling)
Chain 2 Iteration: 1900 / 2500 [ 76%] (Sampling)
Chain 1 Iteration: 1700 / 2500 [ 68%] (Sampling)
Chain 3 Iteration: 2000 / 2500 [ 80%] (Sampling)
Chain 4 Iteration: 1700 / 2500 [ 68%] (Sampling)
Chain 2 Iteration: 2000 / 2500 [ 80%] (Sampling)
Chain 3 Iteration: 2100 / 2500 [ 84%] (Sampling)
Chain 1 Iteration: 1800 / 2500 [ 72%] (Sampling)
Chain 2 Iteration: 2100 / 2500 [ 84%] (Sampling)
Chain 4 Iteration: 1800 / 2500 [ 72%] (Sampling)
Chain 3 Iteration: 2200 / 2500 [ 88%] (Sampling)
Chain 1 Iteration: 1900 / 2500 [ 76%] (Sampling)
Chain 2 Iteration: 2200 / 2500 [ 88%] (Sampling)
Chain 4 Iteration: 1900 / 2500 [ 76%] (Sampling)
Chain 3 Iteration: 2300 / 2500 [ 92%] (Sampling)
Chain 2 Iteration: 2300 / 2500 [ 92%] (Sampling)
Chain 1 Iteration: 2000 / 2500 [ 80%] (Sampling)
Chain 3 Iteration: 2400 / 2500 [ 96%] (Sampling)
Chain 4 Iteration: 2000 / 2500 [ 80%] (Sampling)
Chain 2 Iteration: 2400 / 2500 [ 96%] (Sampling)
Chain 1 Iteration: 2100 / 2500 [ 84%] (Sampling)
Chain 3 Iteration: 2500 / 2500 [100%] (Sampling)
Chain 3 finished in 1407.6 seconds.
Chain 4 Iteration: 2100 / 2500 [ 84%] (Sampling)
Chain 2 Iteration: 2500 / 2500 [100%] (Sampling)
Chain 2 finished in 1439.6 seconds.
Chain 1 Iteration: 2200 / 2500 [ 88%] (Sampling)
Chain 4 Iteration: 2200 / 2500 [ 88%] (Sampling)
Chain 1 Iteration: 2300 / 2500 [ 92%] (Sampling)
Chain 4 Iteration: 2300 / 2500 [ 92%] (Sampling)
Chain 1 Iteration: 2400 / 2500 [ 96%] (Sampling)
Chain 4 Iteration: 2400 / 2500 [ 96%] (Sampling)
Chain 1 Iteration: 2500 / 2500 [100%] (Sampling)
Chain 1 finished in 1647.7 seconds.
Chain 4 Iteration: 2500 / 2500 [100%] (Sampling)
Chain 4 finished in 1664.9 seconds.
All 4 chains finished successfully.
Mean chain execution time: 1539.9 seconds.
Total execution time: 1665.3 seconds.rethinking::precis(m_12h5_c, depth = 2) mean sd 5.5% 94.5% rhat ess_bulk
bCG -0.20417818 0.08744232 -0.34468970 -0.06592429 1.000636 6145.044
bIC -1.25734865 0.09612089 -1.41234385 -1.10580890 1.000253 5585.281
bIA -0.43836773 0.07933192 -0.56619098 -0.31166813 1.000734 4872.344
bC -0.23549425 0.08120475 -0.36358841 -0.10748190 1.000452 4706.627
bI -0.29435282 0.05657062 -0.38414999 -0.20282765 1.000799 4496.050
bA -0.47768823 0.05392764 -0.56410149 -0.39132923 1.000873 4576.789
bG 0.61098031 0.03995077 0.54615368 0.67501506 1.000375 7219.784
cutpoints[1] -2.33589338 0.05458354 -2.42274330 -2.24875670 1.000762 4100.988
cutpoints[2] -1.64062373 0.05059127 -1.72229110 -1.55914000 1.000382 4246.416
cutpoints[3] -1.03959713 0.04903970 -1.11780000 -0.96102882 1.000335 4321.472
cutpoints[4] 0.01791313 0.04805523 -0.05947155 0.09519794 1.000305 4324.148
cutpoints[5] 0.70730797 0.04891564 0.62964150 0.78563671 1.000301 4310.205
cutpoints[6] 1.63461957 0.05173414 1.55143945 1.71593550 1.000396 4655.616Finally, a model with an effect of gender, an interaction between gender and contact, and a three-way interaction between gender, contact, and interaction. This model took about 35 mins (2041.2 seconds).
m_12h5_d <- rethinking::ulam(
alist(
R ~ dordlogit(phi, cutpoints),
phi <- bG * G + bA * A + BC * C + BI * I,
BC <- bC + bCG * G,
BI <- bI + bIA * A + bIC * C + bIG * G + bIGC * G * C,
c(bG, bA, bI, bC, bIA, bIC, bCG, bIG, bIGC) ~ dnorm(0, 0.5),
cutpoints ~ dnorm(0, 1.5)
),
data = dt,
chains = 4, cores = 4,
iter = 2500, warmup = 500,
log_lik = TRUE
)Running MCMC with 4 parallel chains, with 1 thread(s) per chain...Chain 1 Iteration: 1 / 2500 [ 0%] (Warmup) Chain 2 Iteration: 1 / 2500 [ 0%] (Warmup) Chain 3 Iteration: 1 / 2500 [ 0%] (Warmup) Chain 4 Iteration: 1 / 2500 [ 0%] (Warmup) Chain 1 Iteration: 100 / 2500 [ 4%] (Warmup)
Chain 2 Iteration: 100 / 2500 [ 4%] (Warmup)
Chain 4 Iteration: 100 / 2500 [ 4%] (Warmup)
Chain 3 Iteration: 100 / 2500 [ 4%] (Warmup)
Chain 3 Iteration: 200 / 2500 [ 8%] (Warmup)
Chain 4 Iteration: 200 / 2500 [ 8%] (Warmup)
Chain 1 Iteration: 200 / 2500 [ 8%] (Warmup)
Chain 2 Iteration: 200 / 2500 [ 8%] (Warmup)
Chain 3 Iteration: 300 / 2500 [ 12%] (Warmup)
Chain 4 Iteration: 300 / 2500 [ 12%] (Warmup)
Chain 1 Iteration: 300 / 2500 [ 12%] (Warmup)
Chain 2 Iteration: 300 / 2500 [ 12%] (Warmup)
Chain 3 Iteration: 400 / 2500 [ 16%] (Warmup)
Chain 4 Iteration: 400 / 2500 [ 16%] (Warmup)
Chain 1 Iteration: 400 / 2500 [ 16%] (Warmup)
Chain 2 Iteration: 400 / 2500 [ 16%] (Warmup)
Chain 4 Iteration: 500 / 2500 [ 20%] (Warmup)
Chain 4 Iteration: 501 / 2500 [ 20%] (Sampling)
Chain 1 Iteration: 500 / 2500 [ 20%] (Warmup)
Chain 1 Iteration: 501 / 2500 [ 20%] (Sampling)
Chain 3 Iteration: 500 / 2500 [ 20%] (Warmup)
Chain 3 Iteration: 501 / 2500 [ 20%] (Sampling)
Chain 2 Iteration: 500 / 2500 [ 20%] (Warmup)
Chain 2 Iteration: 501 / 2500 [ 20%] (Sampling)
Chain 1 Iteration: 600 / 2500 [ 24%] (Sampling)
Chain 4 Iteration: 600 / 2500 [ 24%] (Sampling)
Chain 3 Iteration: 600 / 2500 [ 24%] (Sampling)
Chain 2 Iteration: 600 / 2500 [ 24%] (Sampling)
Chain 1 Iteration: 700 / 2500 [ 28%] (Sampling)
Chain 3 Iteration: 700 / 2500 [ 28%] (Sampling)
Chain 4 Iteration: 700 / 2500 [ 28%] (Sampling)
Chain 2 Iteration: 700 / 2500 [ 28%] (Sampling)
Chain 1 Iteration: 800 / 2500 [ 32%] (Sampling)
Chain 3 Iteration: 800 / 2500 [ 32%] (Sampling)
Chain 4 Iteration: 800 / 2500 [ 32%] (Sampling)
Chain 2 Iteration: 800 / 2500 [ 32%] (Sampling)
Chain 1 Iteration: 900 / 2500 [ 36%] (Sampling)
Chain 3 Iteration: 900 / 2500 [ 36%] (Sampling)
Chain 4 Iteration: 900 / 2500 [ 36%] (Sampling)
Chain 2 Iteration: 900 / 2500 [ 36%] (Sampling)
Chain 1 Iteration: 1000 / 2500 [ 40%] (Sampling)
Chain 3 Iteration: 1000 / 2500 [ 40%] (Sampling)
Chain 4 Iteration: 1000 / 2500 [ 40%] (Sampling)
Chain 2 Iteration: 1000 / 2500 [ 40%] (Sampling)
Chain 1 Iteration: 1100 / 2500 [ 44%] (Sampling)
Chain 3 Iteration: 1100 / 2500 [ 44%] (Sampling)
Chain 4 Iteration: 1100 / 2500 [ 44%] (Sampling)
Chain 2 Iteration: 1100 / 2500 [ 44%] (Sampling)
Chain 1 Iteration: 1200 / 2500 [ 48%] (Sampling)
Chain 3 Iteration: 1200 / 2500 [ 48%] (Sampling)
Chain 4 Iteration: 1200 / 2500 [ 48%] (Sampling)
Chain 2 Iteration: 1200 / 2500 [ 48%] (Sampling)
Chain 1 Iteration: 1300 / 2500 [ 52%] (Sampling)
Chain 3 Iteration: 1300 / 2500 [ 52%] (Sampling)
Chain 4 Iteration: 1300 / 2500 [ 52%] (Sampling)
Chain 1 Iteration: 1400 / 2500 [ 56%] (Sampling)
Chain 2 Iteration: 1300 / 2500 [ 52%] (Sampling)
Chain 3 Iteration: 1400 / 2500 [ 56%] (Sampling)
Chain 1 Iteration: 1500 / 2500 [ 60%] (Sampling)
Chain 4 Iteration: 1400 / 2500 [ 56%] (Sampling)
Chain 2 Iteration: 1400 / 2500 [ 56%] (Sampling)
Chain 3 Iteration: 1500 / 2500 [ 60%] (Sampling)
Chain 1 Iteration: 1600 / 2500 [ 64%] (Sampling)
Chain 2 Iteration: 1500 / 2500 [ 60%] (Sampling)
Chain 4 Iteration: 1500 / 2500 [ 60%] (Sampling)
Chain 3 Iteration: 1600 / 2500 [ 64%] (Sampling)
Chain 1 Iteration: 1700 / 2500 [ 68%] (Sampling)
Chain 4 Iteration: 1600 / 2500 [ 64%] (Sampling)
Chain 3 Iteration: 1700 / 2500 [ 68%] (Sampling)
Chain 2 Iteration: 1600 / 2500 [ 64%] (Sampling)
Chain 1 Iteration: 1800 / 2500 [ 72%] (Sampling)
Chain 3 Iteration: 1800 / 2500 [ 72%] (Sampling)
Chain 4 Iteration: 1700 / 2500 [ 68%] (Sampling)
Chain 2 Iteration: 1700 / 2500 [ 68%] (Sampling)
Chain 1 Iteration: 1900 / 2500 [ 76%] (Sampling)
Chain 3 Iteration: 1900 / 2500 [ 76%] (Sampling)
Chain 4 Iteration: 1800 / 2500 [ 72%] (Sampling)
Chain 2 Iteration: 1800 / 2500 [ 72%] (Sampling)
Chain 1 Iteration: 2000 / 2500 [ 80%] (Sampling)
Chain 3 Iteration: 2000 / 2500 [ 80%] (Sampling)
Chain 4 Iteration: 1900 / 2500 [ 76%] (Sampling)
Chain 2 Iteration: 1900 / 2500 [ 76%] (Sampling)
Chain 1 Iteration: 2100 / 2500 [ 84%] (Sampling)
Chain 3 Iteration: 2100 / 2500 [ 84%] (Sampling)
Chain 4 Iteration: 2000 / 2500 [ 80%] (Sampling)
Chain 2 Iteration: 2000 / 2500 [ 80%] (Sampling)
Chain 1 Iteration: 2200 / 2500 [ 88%] (Sampling)
Chain 3 Iteration: 2200 / 2500 [ 88%] (Sampling)
Chain 4 Iteration: 2100 / 2500 [ 84%] (Sampling)
Chain 2 Iteration: 2100 / 2500 [ 84%] (Sampling)
Chain 1 Iteration: 2300 / 2500 [ 92%] (Sampling)
Chain 3 Iteration: 2300 / 2500 [ 92%] (Sampling)
Chain 4 Iteration: 2200 / 2500 [ 88%] (Sampling)
Chain 2 Iteration: 2200 / 2500 [ 88%] (Sampling)
Chain 1 Iteration: 2400 / 2500 [ 96%] (Sampling)
Chain 3 Iteration: 2400 / 2500 [ 96%] (Sampling)
Chain 4 Iteration: 2300 / 2500 [ 92%] (Sampling)
Chain 2 Iteration: 2300 / 2500 [ 92%] (Sampling)
Chain 1 Iteration: 2500 / 2500 [100%] (Sampling)
Chain 1 finished in 1764.3 seconds.
Chain 3 Iteration: 2500 / 2500 [100%] (Sampling)
Chain 3 finished in 1781.4 seconds.
Chain 4 Iteration: 2400 / 2500 [ 96%] (Sampling)
Chain 2 Iteration: 2400 / 2500 [ 96%] (Sampling)
Chain 4 Iteration: 2500 / 2500 [100%] (Sampling)
Chain 4 finished in 1892.6 seconds.
Chain 2 Iteration: 2500 / 2500 [100%] (Sampling)
Chain 2 finished in 1894.2 seconds.
All 4 chains finished successfully.
Mean chain execution time: 1833.1 seconds.
Total execution time: 1894.6 seconds.rethinking::precis(m_12h5_d, depth = 2) mean sd 5.5% 94.5% rhat ess_bulk
bIGC -0.20915848 0.16203422 -0.46306556 0.05189080 1.000977 5130.967
bIG -0.04129599 0.07683592 -0.16305000 0.08151255 1.000624 4976.676
bCG -0.10832569 0.11413864 -0.29232876 0.07244840 1.001041 5360.522
bIC -1.14701327 0.12813137 -1.35257200 -0.94925872 1.000789 4539.290
bIA -0.43934379 0.07883742 -0.56429324 -0.31267045 1.000495 5611.090
bC -0.28623308 0.09085992 -0.43175911 -0.13914166 1.000540 4790.100
bI -0.27101024 0.06951654 -0.38317433 -0.15993334 1.000356 4115.908
bA -0.47785710 0.05380390 -0.56462746 -0.39212190 1.001671 5209.883
bG 0.63165057 0.05241401 0.54864839 0.71488217 1.000929 4912.017
cutpoints[1] -2.32536127 0.05777867 -2.41784165 -2.23367505 1.000504 4557.644
cutpoints[2] -1.63003927 0.05445481 -1.71839220 -1.54441340 1.001403 4509.601
cutpoints[3] -1.02915457 0.05277978 -1.11407770 -0.94490379 1.001090 4487.989
cutpoints[4] 0.02898323 0.05184231 -0.05530192 0.11034854 1.001050 4470.520
cutpoints[5] 0.71920408 0.05281163 0.63357380 0.80290164 1.001061 4649.001
cutpoints[6] 1.64670995 0.05578431 1.55819945 1.73646660 1.000891 4976.135First let’s compare all of the models with WAIC, cause for some reason I get an error when I try to do PSIS here.
rethinking::compare(
m_12h5_a, m_12h5_b, m_12h5_c, m_12h5_d
) WAIC SE dWAIC dSE pWAIC weight
m_12h5_c 36669.92 86.75916 0.000000 NA 12.76052 6.130660e-01
m_12h5_d 36671.39 87.15328 1.474024 3.302479 14.55312 2.933776e-01
m_12h5_b 36673.68 86.45078 3.759817 4.530810 11.88663 9.355638e-02
m_12h5_a 36929.09 80.68957 259.170095 31.415163 10.89760 3.231739e-57Well, once we include gender as a main effect the models are all exactly the same, indicating that either the interaction doesn’t help us predict anything, or we don’t have enough data to get a compelling estiamte of the interaction.
So there are some differences between men and women, but the idea that these differences are caused by a difference in response to contact is not supported by the data. Since these models took a long time and the interactions didn’t seem to do anything, I don’t feel terribly motivated to do anything else for this problem, even though I know PSIS isn’t the best justification for this, we should actually compute contrasts and see what happens. But I don’t really want to do that.
12H6
Now (for some reason before we go back to work on the Trolley data again) we’ll take a look at some national parks fishing data.
data(Fish, package = "rethinking")
dat_fish <- list(
F = Fish$fish_caught,
B = Fish$livebait,
C = Fish$camper,
P = Fish$persons,
K = Fish$child,
H = Fish$hours
)We want to fit a zero-inflated model of the number of fish caught by a visitor who came to the park. Since the individuals visited the park for different amounts of time, we need to model the rate of fish per hour instead of just the total number of fish caught per person.
We have a few different explanatory variables as well – we should definitely include whether someone used live bait as a predictor in our model. Honestly, I think (non-casually, without drawing a DAG to deal with confounders, since I’m feeling lazy on this problem) we should probably include most of the available predictors – people with live bait probably catch more fish, people with campers I think are more likely to have fishing experience, so we’ll include that, and groups with kids are less likely to fish since kids get bored during fishing. And of course groups with more adults that fish will probably catch more fish, although I think it’s possible that groups with more adults are also less likely to fish in general, because fishing is very often a solo activity. So for now, I’ll throw all four covariates in both the exposure and the mean model, and hopefully Richard won’t chastise me too much in the solutions manual.
Since I don’t want the model to take a long time to sample, I’m including number of adults and number of kids as linear effects in the model, although in a real analysis we would want to consider this as an ordered categorical predictor also.
dat_fish$log_hours <- log(dat_fish$H)
m_12h6 <- rethinking::ulam(
alist(
F ~ dzipois(p, lambda),
logit(p) <- a_p + bB_p * B + bC_p * C + bP_p * P + bK_p * K,
log(lambda) <- a_l + bB_l * B + bC_l * C + bP_l * P + bK_l * K + log_hours,
a_p ~ dnorm(0, 1.5),
c(bB_p, bC_p, bP_p, bK_p) ~ dnorm(0, 0.5),
a_l ~ dnorm(3, 0.5),
c(bB_l, bC_l, bP_l, bK_l) ~ dnorm(0, 1)
),
data = dat_fish,
chains = 4, cores = 4,
iter = 2500, warmup = 500,
# we don't need this here but I didn't want to have to rerun
# if I ended up needing it
log_lik = TRUE
)Running MCMC with 4 parallel chains, with 1 thread(s) per chain...
Chain 1 Iteration: 1 / 2500 [ 0%] (Warmup)
Chain 2 Iteration: 1 / 2500 [ 0%] (Warmup)
Chain 3 Iteration: 1 / 2500 [ 0%] (Warmup)
Chain 4 Iteration: 1 / 2500 [ 0%] (Warmup)
Chain 3 Iteration: 100 / 2500 [ 4%] (Warmup)
Chain 2 Iteration: 100 / 2500 [ 4%] (Warmup)
Chain 4 Iteration: 100 / 2500 [ 4%] (Warmup)
Chain 1 Iteration: 100 / 2500 [ 4%] (Warmup)
Chain 3 Iteration: 200 / 2500 [ 8%] (Warmup)
Chain 2 Iteration: 200 / 2500 [ 8%] (Warmup)
Chain 4 Iteration: 200 / 2500 [ 8%] (Warmup)
Chain 1 Iteration: 200 / 2500 [ 8%] (Warmup)
Chain 3 Iteration: 300 / 2500 [ 12%] (Warmup)
Chain 4 Iteration: 300 / 2500 [ 12%] (Warmup)
Chain 2 Iteration: 300 / 2500 [ 12%] (Warmup)
Chain 1 Iteration: 300 / 2500 [ 12%] (Warmup)
Chain 3 Iteration: 400 / 2500 [ 16%] (Warmup)
Chain 2 Iteration: 400 / 2500 [ 16%] (Warmup)
Chain 4 Iteration: 400 / 2500 [ 16%] (Warmup)
Chain 1 Iteration: 400 / 2500 [ 16%] (Warmup)
Chain 3 Iteration: 500 / 2500 [ 20%] (Warmup)
Chain 3 Iteration: 501 / 2500 [ 20%] (Sampling)
Chain 4 Iteration: 500 / 2500 [ 20%] (Warmup)
Chain 4 Iteration: 501 / 2500 [ 20%] (Sampling)
Chain 2 Iteration: 500 / 2500 [ 20%] (Warmup)
Chain 1 Iteration: 500 / 2500 [ 20%] (Warmup)
Chain 2 Iteration: 501 / 2500 [ 20%] (Sampling)
Chain 1 Iteration: 501 / 2500 [ 20%] (Sampling)
Chain 3 Iteration: 600 / 2500 [ 24%] (Sampling)
Chain 4 Iteration: 600 / 2500 [ 24%] (Sampling)
Chain 1 Iteration: 600 / 2500 [ 24%] (Sampling)
Chain 2 Iteration: 600 / 2500 [ 24%] (Sampling)
Chain 3 Iteration: 700 / 2500 [ 28%] (Sampling)
Chain 4 Iteration: 700 / 2500 [ 28%] (Sampling)
Chain 1 Iteration: 700 / 2500 [ 28%] (Sampling)
Chain 2 Iteration: 700 / 2500 [ 28%] (Sampling)
Chain 3 Iteration: 800 / 2500 [ 32%] (Sampling)
Chain 4 Iteration: 800 / 2500 [ 32%] (Sampling)
Chain 1 Iteration: 800 / 2500 [ 32%] (Sampling)
Chain 2 Iteration: 800 / 2500 [ 32%] (Sampling)
Chain 3 Iteration: 900 / 2500 [ 36%] (Sampling)
Chain 4 Iteration: 900 / 2500 [ 36%] (Sampling)
Chain 1 Iteration: 900 / 2500 [ 36%] (Sampling)
Chain 4 Iteration: 1000 / 2500 [ 40%] (Sampling)
Chain 3 Iteration: 1000 / 2500 [ 40%] (Sampling)
Chain 2 Iteration: 900 / 2500 [ 36%] (Sampling)
Chain 1 Iteration: 1000 / 2500 [ 40%] (Sampling)
Chain 4 Iteration: 1100 / 2500 [ 44%] (Sampling)
Chain 3 Iteration: 1100 / 2500 [ 44%] (Sampling)
Chain 2 Iteration: 1000 / 2500 [ 40%] (Sampling)
Chain 1 Iteration: 1100 / 2500 [ 44%] (Sampling)
Chain 4 Iteration: 1200 / 2500 [ 48%] (Sampling)
Chain 3 Iteration: 1200 / 2500 [ 48%] (Sampling)
Chain 4 Iteration: 1300 / 2500 [ 52%] (Sampling)
Chain 2 Iteration: 1100 / 2500 [ 44%] (Sampling)
Chain 1 Iteration: 1200 / 2500 [ 48%] (Sampling)
Chain 3 Iteration: 1300 / 2500 [ 52%] (Sampling)
Chain 4 Iteration: 1400 / 2500 [ 56%] (Sampling)
Chain 1 Iteration: 1300 / 2500 [ 52%] (Sampling)
Chain 2 Iteration: 1200 / 2500 [ 48%] (Sampling)
Chain 3 Iteration: 1400 / 2500 [ 56%] (Sampling)
Chain 4 Iteration: 1500 / 2500 [ 60%] (Sampling)
Chain 1 Iteration: 1400 / 2500 [ 56%] (Sampling)
Chain 2 Iteration: 1300 / 2500 [ 52%] (Sampling)
Chain 3 Iteration: 1500 / 2500 [ 60%] (Sampling)
Chain 4 Iteration: 1600 / 2500 [ 64%] (Sampling)
Chain 1 Iteration: 1500 / 2500 [ 60%] (Sampling)
Chain 2 Iteration: 1400 / 2500 [ 56%] (Sampling)
Chain 3 Iteration: 1600 / 2500 [ 64%] (Sampling)
Chain 4 Iteration: 1700 / 2500 [ 68%] (Sampling)
Chain 1 Iteration: 1600 / 2500 [ 64%] (Sampling)
Chain 3 Iteration: 1700 / 2500 [ 68%] (Sampling)
Chain 4 Iteration: 1800 / 2500 [ 72%] (Sampling)
Chain 2 Iteration: 1500 / 2500 [ 60%] (Sampling)
Chain 1 Iteration: 1700 / 2500 [ 68%] (Sampling)
Chain 3 Iteration: 1800 / 2500 [ 72%] (Sampling)
Chain 4 Iteration: 1900 / 2500 [ 76%] (Sampling)
Chain 2 Iteration: 1600 / 2500 [ 64%] (Sampling)
Chain 1 Iteration: 1800 / 2500 [ 72%] (Sampling)
Chain 4 Iteration: 2000 / 2500 [ 80%] (Sampling)
Chain 3 Iteration: 1900 / 2500 [ 76%] (Sampling)
Chain 1 Iteration: 1900 / 2500 [ 76%] (Sampling)
Chain 2 Iteration: 1700 / 2500 [ 68%] (Sampling)
Chain 4 Iteration: 2100 / 2500 [ 84%] (Sampling)
Chain 3 Iteration: 2000 / 2500 [ 80%] (Sampling)
Chain 1 Iteration: 2000 / 2500 [ 80%] (Sampling)
Chain 4 Iteration: 2200 / 2500 [ 88%] (Sampling)
Chain 2 Iteration: 1800 / 2500 [ 72%] (Sampling)
Chain 3 Iteration: 2100 / 2500 [ 84%] (Sampling)
Chain 1 Iteration: 2100 / 2500 [ 84%] (Sampling)
Chain 4 Iteration: 2300 / 2500 [ 92%] (Sampling)
Chain 3 Iteration: 2200 / 2500 [ 88%] (Sampling)
Chain 2 Iteration: 1900 / 2500 [ 76%] (Sampling)
Chain 4 Iteration: 2400 / 2500 [ 96%] (Sampling)
Chain 1 Iteration: 2200 / 2500 [ 88%] (Sampling)
Chain 3 Iteration: 2300 / 2500 [ 92%] (Sampling)
Chain 2 Iteration: 2000 / 2500 [ 80%] (Sampling)
Chain 4 Iteration: 2500 / 2500 [100%] (Sampling)
Chain 4 finished in 21.4 seconds.
Chain 1 Iteration: 2300 / 2500 [ 92%] (Sampling)
Chain 3 Iteration: 2400 / 2500 [ 96%] (Sampling)
Chain 2 Iteration: 2100 / 2500 [ 84%] (Sampling)
Chain 1 Iteration: 2400 / 2500 [ 96%] (Sampling)
Chain 3 Iteration: 2500 / 2500 [100%] (Sampling)
Chain 3 finished in 22.7 seconds.
Chain 2 Iteration: 2200 / 2500 [ 88%] (Sampling)
Chain 1 Iteration: 2500 / 2500 [100%] (Sampling)
Chain 1 finished in 23.2 seconds.
Chain 2 Iteration: 2300 / 2500 [ 92%] (Sampling)
Chain 2 Iteration: 2400 / 2500 [ 96%] (Sampling)
Chain 2 Iteration: 2500 / 2500 [100%] (Sampling)
Chain 2 finished in 25.2 seconds.
All 4 chains finished successfully.
Mean chain execution time: 23.1 seconds.
Total execution time: 25.3 seconds.rethinking::precis(m_12h6) mean sd 5.5% 94.5% rhat ess_bulk
a_p 0.9677036 0.59267036 0.02749316 1.9096735 1.0009029 4011.205
bK_p 0.6129267 0.41633629 -0.09809129 1.2251405 1.0005225 6223.990
bP_p -0.7786110 0.21297643 -1.12641090 -0.4493270 1.0007712 4647.999
bC_p -0.2018418 0.35712440 -0.76129502 0.3737356 0.9999112 7025.015
bB_p -0.3187083 0.39272118 -0.94252827 0.3059171 1.0010375 6563.091
a_l -2.2162689 0.19033810 -2.52422275 -1.9120089 1.0009656 4952.409
bK_l 0.5292179 0.09173787 0.37994180 0.6751814 1.0002748 7190.174
bP_l 0.5968661 0.03764793 0.53746629 0.6584932 1.0004584 6313.693
bC_l -0.4878927 0.08939923 -0.63108832 -0.3429339 1.0003216 8290.810
bB_l 0.6494087 0.16087558 0.40222052 0.9139753 1.0003291 6088.106We can see from the results that interestingly the only variable that appears to strongly affect the probability that someone went fishing is \(P\), the number of adults in the group. If there are more adults present, the group was less likely to fish. It’s possible that \(K\), the number of children present, also had an effect on the probability of fishing, although our model doesn’t completely rule out this variable having no effect or a small negative effect.
In terms of affecting the number of fish caught (per hour spent in the park) assuming someone went fishing, all four variables are important, as we might expect. More kids and more adults in the group both increase the number of fish caught, because there are more chances to catch fish, even if kids are generally a little bit worse at fishing (although not that much, judging from the effects we observed). If someone brought a camper they caught less fish, presumably because they were spending time doing non-fishing activities, and if they used live bait they tended to catch more fish as we would expect.
The last thing I’ll do for this problem is quickly check the posterior predictions.
graphics.off()
layout(matrix(1:6, nrow = 2, byrow = TRUE))
rethinking::postcheck(m_12h6, window = 42)Although the plots are kind of small, we can see that many predictions appear to be pretty accurate. However, there are a few people who caught more fish than we expected, and a few who caught less fish than we expected, so maybe a zero-inflated gamma-Poisson model would be more appropriate.
12H7
If age affects college education status (older people are more likely to have higher education statuses, because young people couldn’t have attained the same ones by then), and age also affects response to Trolley problems, then age would be a confounder on the effect of college education status on Trolly problem ratings. The DAG would look like this.
graphics.off()
layout(1)
m12h7_dag <- dagitty::dagitty(
"dag {
E <- A -> R <- E
}"
)
dagitty::coordinates(m12h7_dag) <- list(
x = c(A = 1, E = 3, R = 2),
y = c(A = 1, E = 1, R = 2)
)
plot(m12h7_dag)To evaluate the effect of education on the response, now we need to control for age at the same time. It’s possible that there could be an interaction between age and education as well, but we’ll ignore that for this problem. So, we’ll build a model that treats age as a continuous, linear effect – that probably isn’t ideal, we probably want a spline or something, but we’ll ignore that for now since we already have to deal with an ordered categorical predictor which can make the model a bit slow.
edu_levels <- c(6, 1, 8, 4, 7, 2, 5, 3)
dt2 <- list(
R = Trolley$response,
A = Trolley$age,
E = as.integer(edu_levels[Trolley$edu]),
action = Trolley$action,
intention = Trolley$intention,
contact = Trolley$contact,
alpha = rep(2, 7)
)
m_12h7 <- rethinking::ulam(
alist(
R ~ dordlogit(phi, kappa),
phi <- bE * sum(delta_j[1:E]) + bA * A + b_ac * action + b_co * contact +
BI * intention,
BI <- bI + bIAc * action + bIC * contact,
kappa ~ dnorm(0, 1.5),
c(bE, bA, b_ac, b_co, bI, bIAc, bIC) ~ dnorm(0, 0.5),
vector[8]: delta_j <<- append_row(0, delta),
simplex[7]: delta ~ dirichlet(alpha)
),
data = dt2,
chains = 4, cores = 4,
iter = 2500, warmup = 500,
# we don't need this here but I didn't want to have to rerun
# if I ended up needing it
log_lik = TRUE
)Running MCMC with 4 parallel chains, with 1 thread(s) per chain...Chain 1 Iteration: 1 / 2500 [ 0%] (Warmup) Chain 2 Iteration: 1 / 2500 [ 0%] (Warmup) Chain 3 Iteration: 1 / 2500 [ 0%] (Warmup) Chain 4 Iteration: 1 / 2500 [ 0%] (Warmup) Chain 2 Iteration: 100 / 2500 [ 4%] (Warmup)
Chain 1 Iteration: 100 / 2500 [ 4%] (Warmup)
Chain 2 Iteration: 200 / 2500 [ 8%] (Warmup)
Chain 1 Iteration: 200 / 2500 [ 8%] (Warmup)
Chain 4 Iteration: 100 / 2500 [ 4%] (Warmup)
Chain 3 Iteration: 100 / 2500 [ 4%] (Warmup)
Chain 2 Iteration: 300 / 2500 [ 12%] (Warmup)
Chain 1 Iteration: 300 / 2500 [ 12%] (Warmup)
Chain 2 Iteration: 400 / 2500 [ 16%] (Warmup)
Chain 1 Iteration: 400 / 2500 [ 16%] (Warmup)
Chain 2 Iteration: 500 / 2500 [ 20%] (Warmup)
Chain 2 Iteration: 501 / 2500 [ 20%] (Sampling)
Chain 4 Iteration: 200 / 2500 [ 8%] (Warmup)
Chain 1 Iteration: 500 / 2500 [ 20%] (Warmup)
Chain 1 Iteration: 501 / 2500 [ 20%] (Sampling)
Chain 2 Iteration: 600 / 2500 [ 24%] (Sampling)
Chain 3 Iteration: 200 / 2500 [ 8%] (Warmup)
Chain 1 Iteration: 600 / 2500 [ 24%] (Sampling)
Chain 4 Iteration: 300 / 2500 [ 12%] (Warmup)
Chain 2 Iteration: 700 / 2500 [ 28%] (Sampling)
Chain 1 Iteration: 700 / 2500 [ 28%] (Sampling)
Chain 3 Iteration: 300 / 2500 [ 12%] (Warmup)
Chain 4 Iteration: 400 / 2500 [ 16%] (Warmup)
Chain 2 Iteration: 800 / 2500 [ 32%] (Sampling)
Chain 1 Iteration: 800 / 2500 [ 32%] (Sampling)
Chain 2 Iteration: 900 / 2500 [ 36%] (Sampling)
Chain 3 Iteration: 400 / 2500 [ 16%] (Warmup)
Chain 4 Iteration: 500 / 2500 [ 20%] (Warmup)
Chain 4 Iteration: 501 / 2500 [ 20%] (Sampling)
Chain 1 Iteration: 900 / 2500 [ 36%] (Sampling)
Chain 2 Iteration: 1000 / 2500 [ 40%] (Sampling)
Chain 3 Iteration: 500 / 2500 [ 20%] (Warmup)
Chain 3 Iteration: 501 / 2500 [ 20%] (Sampling)
Chain 4 Iteration: 600 / 2500 [ 24%] (Sampling)
Chain 1 Iteration: 1000 / 2500 [ 40%] (Sampling)
Chain 2 Iteration: 1100 / 2500 [ 44%] (Sampling)
Chain 4 Iteration: 700 / 2500 [ 28%] (Sampling)
Chain 3 Iteration: 600 / 2500 [ 24%] (Sampling)
Chain 1 Iteration: 1100 / 2500 [ 44%] (Sampling)
Chain 4 Iteration: 800 / 2500 [ 32%] (Sampling)
Chain 2 Iteration: 1200 / 2500 [ 48%] (Sampling)
Chain 3 Iteration: 700 / 2500 [ 28%] (Sampling)
Chain 1 Iteration: 1200 / 2500 [ 48%] (Sampling)
Chain 4 Iteration: 900 / 2500 [ 36%] (Sampling)
Chain 2 Iteration: 1300 / 2500 [ 52%] (Sampling)
Chain 3 Iteration: 800 / 2500 [ 32%] (Sampling)
Chain 1 Iteration: 1300 / 2500 [ 52%] (Sampling)
Chain 4 Iteration: 1000 / 2500 [ 40%] (Sampling)
Chain 2 Iteration: 1400 / 2500 [ 56%] (Sampling)
Chain 3 Iteration: 900 / 2500 [ 36%] (Sampling)
Chain 1 Iteration: 1400 / 2500 [ 56%] (Sampling)
Chain 4 Iteration: 1100 / 2500 [ 44%] (Sampling)
Chain 2 Iteration: 1500 / 2500 [ 60%] (Sampling)
Chain 3 Iteration: 1000 / 2500 [ 40%] (Sampling)
Chain 4 Iteration: 1200 / 2500 [ 48%] (Sampling)
Chain 1 Iteration: 1500 / 2500 [ 60%] (Sampling)
Chain 3 Iteration: 1100 / 2500 [ 44%] (Sampling)
Chain 2 Iteration: 1600 / 2500 [ 64%] (Sampling)
Chain 4 Iteration: 1300 / 2500 [ 52%] (Sampling)
Chain 1 Iteration: 1600 / 2500 [ 64%] (Sampling)
Chain 3 Iteration: 1200 / 2500 [ 48%] (Sampling)
Chain 2 Iteration: 1700 / 2500 [ 68%] (Sampling)
Chain 4 Iteration: 1400 / 2500 [ 56%] (Sampling)
Chain 1 Iteration: 1700 / 2500 [ 68%] (Sampling)
Chain 3 Iteration: 1300 / 2500 [ 52%] (Sampling)
Chain 2 Iteration: 1800 / 2500 [ 72%] (Sampling)
Chain 4 Iteration: 1500 / 2500 [ 60%] (Sampling)
Chain 1 Iteration: 1800 / 2500 [ 72%] (Sampling)
Chain 3 Iteration: 1400 / 2500 [ 56%] (Sampling)
Chain 4 Iteration: 1600 / 2500 [ 64%] (Sampling)
Chain 2 Iteration: 1900 / 2500 [ 76%] (Sampling)
Chain 1 Iteration: 1900 / 2500 [ 76%] (Sampling)
Chain 4 Iteration: 1700 / 2500 [ 68%] (Sampling)
Chain 3 Iteration: 1500 / 2500 [ 60%] (Sampling)
Chain 2 Iteration: 2000 / 2500 [ 80%] (Sampling)
Chain 1 Iteration: 2000 / 2500 [ 80%] (Sampling)
Chain 4 Iteration: 1800 / 2500 [ 72%] (Sampling)
Chain 3 Iteration: 1600 / 2500 [ 64%] (Sampling)
Chain 2 Iteration: 2100 / 2500 [ 84%] (Sampling)
Chain 1 Iteration: 2100 / 2500 [ 84%] (Sampling)
Chain 4 Iteration: 1900 / 2500 [ 76%] (Sampling)
Chain 3 Iteration: 1700 / 2500 [ 68%] (Sampling)
Chain 2 Iteration: 2200 / 2500 [ 88%] (Sampling)
Chain 1 Iteration: 2200 / 2500 [ 88%] (Sampling)
Chain 4 Iteration: 2000 / 2500 [ 80%] (Sampling)
Chain 3 Iteration: 1800 / 2500 [ 72%] (Sampling)
Chain 2 Iteration: 2300 / 2500 [ 92%] (Sampling)
Chain 4 Iteration: 2100 / 2500 [ 84%] (Sampling)
Chain 1 Iteration: 2300 / 2500 [ 92%] (Sampling)
Chain 3 Iteration: 1900 / 2500 [ 76%] (Sampling)
Chain 2 Iteration: 2400 / 2500 [ 96%] (Sampling)
Chain 4 Iteration: 2200 / 2500 [ 88%] (Sampling)
Chain 1 Iteration: 2400 / 2500 [ 96%] (Sampling)
Chain 3 Iteration: 2000 / 2500 [ 80%] (Sampling)
Chain 2 Iteration: 2500 / 2500 [100%] (Sampling)
Chain 2 finished in 3378.7 seconds.
Chain 4 Iteration: 2300 / 2500 [ 92%] (Sampling)
Chain 1 Iteration: 2500 / 2500 [100%] (Sampling)
Chain 1 finished in 3406.9 seconds.
Chain 3 Iteration: 2100 / 2500 [ 84%] (Sampling)
Chain 4 Iteration: 2400 / 2500 [ 96%] (Sampling)
Chain 3 Iteration: 2200 / 2500 [ 88%] (Sampling)
Chain 4 Iteration: 2500 / 2500 [100%] (Sampling)
Chain 4 finished in 3512.0 seconds.
Chain 3 Iteration: 2300 / 2500 [ 92%] (Sampling)
Chain 3 Iteration: 2400 / 2500 [ 96%] (Sampling)
Chain 3 Iteration: 2500 / 2500 [100%] (Sampling)
Chain 3 finished in 3686.1 seconds.
All 4 chains finished successfully.
Mean chain execution time: 3495.9 seconds.
Total execution time: 3686.6 seconds.rethinking::precis(m_12h7, depth = 2) mean sd 5.5% 94.5% rhat ess_bulk
kappa[1] -2.752678806 0.089115842 -2.894880350 -2.617160000 1.0013081 2545.833
kappa[2] -2.054431159 0.086259999 -2.191567150 -1.923408900 1.0005803 2488.464
kappa[3] -1.458290434 0.084902646 -1.592831100 -1.331689450 1.0008805 2489.386
kappa[4] -0.420138527 0.084263236 -0.553517485 -0.293994590 1.0008968 2459.579
kappa[5] 0.252910339 0.084661639 0.117808370 0.380547695 1.0008512 2496.813
kappa[6] 1.159227962 0.086299108 1.021709450 1.288244950 1.0011499 2559.098
bIC -1.240156522 0.095471073 -1.391193300 -1.083958350 1.0008948 4350.205
bIAc -0.435717166 0.078236799 -0.560618940 -0.310078965 1.0016702 3461.213
bI -0.291313173 0.056706916 -0.381298795 -0.202123890 1.0015062 3249.785
b_co -0.344001187 0.067685171 -0.451091880 -0.236522235 1.0008744 5105.550
b_ac -0.474140421 0.053621147 -0.560519430 -0.389534120 1.0014297 4106.078
bA -0.006948654 0.001502888 -0.009284400 -0.004449103 1.0011767 3323.164
bE 0.221069475 0.121646612 -0.001770296 0.364745165 1.0015548 2021.694
delta[1] 0.113206861 0.074851414 0.023281967 0.249436540 1.0004687 5937.779
delta[2] 0.120768363 0.075331705 0.026410197 0.260251355 1.0006938 8449.987
delta[3] 0.087217305 0.061813173 0.017325423 0.200246935 1.0004378 5615.582
delta[4] 0.068038256 0.056718572 0.011703960 0.169360815 1.0011391 3082.294
delta[5] 0.430431108 0.149070703 0.112904845 0.630933970 1.0009114 2067.112
delta[6] 0.084229199 0.058487223 0.015721033 0.193204375 0.9999023 7376.711
delta[7] 0.096108909 0.065575021 0.018770120 0.213578565 1.0005580 7788.204I’m glad I didn’t make this model any more complicated in terms of age, because it already took like an hour (3759.0 seconds) to sample.
Because education (\(E\)) is a mediator on the path between \(A\) and \(E\), this is the only model we need to fit to estimate the causal effect of \(E\) on \(R\) when age (\(A\)) is a confounder. There is no indirect effect under this causal model, only the direct effect.
Anyways, from the results we can see that the effect of education is overall positive while the effect of age looks like it is quite small. However, I did include age on its natural scale (maybe a bad idea), which has a large range so it’s definitely possible that the effect of age is strong, but hard to compare to the other parameters which are mostly scale-free. But either way we can see that controlling for age reverses the effect of education – so actually, people rate their approval of the stories more highly when they have higher education, but being older leads to lower overall approval ratings.
12H8
If gender influences both education and trolley problem response we might get the following DAG.
m12h8_dag <- dagitty::dagitty(
"dag {
E <- A -> R <- E
E <- G -> R
}"
)
dagitty::coordinates(m12h8_dag) <- list(
x = c(A = 1, E = 2, R = 2, G = 1),
y = c(A = 1, E = 1, R = 2, G = 2)
)
plot(m12h8_dag)
Under this DAG, both age and gender are confounders of the effect of education on trolley problem story responses, but fortunately we can control for both age and gender to close all backdoor paths without opening any colliding paths, and we can estimate the causal effect of education on response under this model.
Let’s go ahead and fit this model and see what happens.
dt2$G <- Trolley$male
m_12h8 <- rethinking::ulam(
alist(
R ~ dordlogit(phi, kappa),
phi <- bE * sum(delta_j[1:E]) + bA * A + b_ac * action + b_co * contact +
BI * intention + bG * G,
BI <- bI + bIAc * action + bIC * contact,
kappa ~ dnorm(0, 1.5),
c(bE, bA, b_ac, b_co, bI, bIAc, bIC, bG) ~ dnorm(0, 0.5),
vector[8]: delta_j <<- append_row(0, delta),
simplex[7]: delta ~ dirichlet(alpha)
),
data = dt2,
chains = 4, cores = 4,
iter = 2500, warmup = 500,
# we don't need this here but I didn't want to have to rerun
# if I ended up needing it
log_lik = TRUE
)Running MCMC with 4 parallel chains, with 1 thread(s) per chain...Chain 1 Iteration: 1 / 2500 [ 0%] (Warmup) Chain 2 Iteration: 1 / 2500 [ 0%] (Warmup) Chain 3 Iteration: 1 / 2500 [ 0%] (Warmup) Chain 4 Iteration: 1 / 2500 [ 0%] (Warmup) Chain 2 Iteration: 100 / 2500 [ 4%] (Warmup)
Chain 4 Iteration: 100 / 2500 [ 4%] (Warmup)
Chain 3 Iteration: 100 / 2500 [ 4%] (Warmup)
Chain 2 Iteration: 200 / 2500 [ 8%] (Warmup)
Chain 1 Iteration: 100 / 2500 [ 4%] (Warmup)
Chain 2 Iteration: 300 / 2500 [ 12%] (Warmup)
Chain 4 Iteration: 200 / 2500 [ 8%] (Warmup)
Chain 3 Iteration: 200 / 2500 [ 8%] (Warmup)
Chain 2 Iteration: 400 / 2500 [ 16%] (Warmup)
Chain 4 Iteration: 300 / 2500 [ 12%] (Warmup)
Chain 2 Iteration: 500 / 2500 [ 20%] (Warmup)
Chain 2 Iteration: 501 / 2500 [ 20%] (Sampling)
Chain 1 Iteration: 200 / 2500 [ 8%] (Warmup)
Chain 3 Iteration: 300 / 2500 [ 12%] (Warmup)
Chain 4 Iteration: 400 / 2500 [ 16%] (Warmup)
Chain 2 Iteration: 600 / 2500 [ 24%] (Sampling)
Chain 3 Iteration: 400 / 2500 [ 16%] (Warmup)
Chain 1 Iteration: 300 / 2500 [ 12%] (Warmup)
Chain 4 Iteration: 500 / 2500 [ 20%] (Warmup)
Chain 4 Iteration: 501 / 2500 [ 20%] (Sampling)
Chain 2 Iteration: 700 / 2500 [ 28%] (Sampling)
Chain 4 Iteration: 600 / 2500 [ 24%] (Sampling)
Chain 3 Iteration: 500 / 2500 [ 20%] (Warmup)
Chain 3 Iteration: 501 / 2500 [ 20%] (Sampling)
Chain 1 Iteration: 400 / 2500 [ 16%] (Warmup)
Chain 2 Iteration: 800 / 2500 [ 32%] (Sampling)
Chain 3 Iteration: 600 / 2500 [ 24%] (Sampling)
Chain 4 Iteration: 700 / 2500 [ 28%] (Sampling)
Chain 1 Iteration: 500 / 2500 [ 20%] (Warmup)
Chain 1 Iteration: 501 / 2500 [ 20%] (Sampling)
Chain 2 Iteration: 900 / 2500 [ 36%] (Sampling)
Chain 3 Iteration: 700 / 2500 [ 28%] (Sampling)
Chain 4 Iteration: 800 / 2500 [ 32%] (Sampling)
Chain 1 Iteration: 600 / 2500 [ 24%] (Sampling)
Chain 2 Iteration: 1000 / 2500 [ 40%] (Sampling)
Chain 3 Iteration: 800 / 2500 [ 32%] (Sampling)
Chain 4 Iteration: 900 / 2500 [ 36%] (Sampling)
Chain 1 Iteration: 700 / 2500 [ 28%] (Sampling)
Chain 2 Iteration: 1100 / 2500 [ 44%] (Sampling)
Chain 3 Iteration: 900 / 2500 [ 36%] (Sampling)
Chain 4 Iteration: 1000 / 2500 [ 40%] (Sampling)
Chain 1 Iteration: 800 / 2500 [ 32%] (Sampling)
Chain 3 Iteration: 1000 / 2500 [ 40%] (Sampling)
Chain 2 Iteration: 1200 / 2500 [ 48%] (Sampling)
Chain 4 Iteration: 1100 / 2500 [ 44%] (Sampling)
Chain 1 Iteration: 900 / 2500 [ 36%] (Sampling)
Chain 3 Iteration: 1100 / 2500 [ 44%] (Sampling)
Chain 2 Iteration: 1300 / 2500 [ 52%] (Sampling)
Chain 4 Iteration: 1200 / 2500 [ 48%] (Sampling)
Chain 3 Iteration: 1200 / 2500 [ 48%] (Sampling)
Chain 1 Iteration: 1000 / 2500 [ 40%] (Sampling)
Chain 4 Iteration: 1300 / 2500 [ 52%] (Sampling)
Chain 2 Iteration: 1400 / 2500 [ 56%] (Sampling)
Chain 3 Iteration: 1300 / 2500 [ 52%] (Sampling)
Chain 1 Iteration: 1100 / 2500 [ 44%] (Sampling)
Chain 4 Iteration: 1400 / 2500 [ 56%] (Sampling)
Chain 2 Iteration: 1500 / 2500 [ 60%] (Sampling)
Chain 3 Iteration: 1400 / 2500 [ 56%] (Sampling)
Chain 1 Iteration: 1200 / 2500 [ 48%] (Sampling)
Chain 4 Iteration: 1500 / 2500 [ 60%] (Sampling)
Chain 3 Iteration: 1500 / 2500 [ 60%] (Sampling)
Chain 2 Iteration: 1600 / 2500 [ 64%] (Sampling)
Chain 1 Iteration: 1300 / 2500 [ 52%] (Sampling)
Chain 4 Iteration: 1600 / 2500 [ 64%] (Sampling)
Chain 3 Iteration: 1600 / 2500 [ 64%] (Sampling)
Chain 2 Iteration: 1700 / 2500 [ 68%] (Sampling)
Chain 1 Iteration: 1400 / 2500 [ 56%] (Sampling)
Chain 4 Iteration: 1700 / 2500 [ 68%] (Sampling)
Chain 3 Iteration: 1700 / 2500 [ 68%] (Sampling)
Chain 1 Iteration: 1500 / 2500 [ 60%] (Sampling)
Chain 2 Iteration: 1800 / 2500 [ 72%] (Sampling)
Chain 4 Iteration: 1800 / 2500 [ 72%] (Sampling)
Chain 3 Iteration: 1800 / 2500 [ 72%] (Sampling)
Chain 1 Iteration: 1600 / 2500 [ 64%] (Sampling)
Chain 2 Iteration: 1900 / 2500 [ 76%] (Sampling)
Chain 4 Iteration: 1900 / 2500 [ 76%] (Sampling)
Chain 3 Iteration: 1900 / 2500 [ 76%] (Sampling)
Chain 1 Iteration: 1700 / 2500 [ 68%] (Sampling)
Chain 4 Iteration: 2000 / 2500 [ 80%] (Sampling)
Chain 2 Iteration: 2000 / 2500 [ 80%] (Sampling)
Chain 3 Iteration: 2000 / 2500 [ 80%] (Sampling)
Chain 1 Iteration: 1800 / 2500 [ 72%] (Sampling)
Chain 3 Iteration: 2100 / 2500 [ 84%] (Sampling)
Chain 4 Iteration: 2100 / 2500 [ 84%] (Sampling)
Chain 2 Iteration: 2100 / 2500 [ 84%] (Sampling)
Chain 1 Iteration: 1900 / 2500 [ 76%] (Sampling)
Chain 3 Iteration: 2200 / 2500 [ 88%] (Sampling)
Chain 4 Iteration: 2200 / 2500 [ 88%] (Sampling)
Chain 2 Iteration: 2200 / 2500 [ 88%] (Sampling)
Chain 1 Iteration: 2000 / 2500 [ 80%] (Sampling)
Chain 3 Iteration: 2300 / 2500 [ 92%] (Sampling)
Chain 4 Iteration: 2300 / 2500 [ 92%] (Sampling)
Chain 2 Iteration: 2300 / 2500 [ 92%] (Sampling)
Chain 1 Iteration: 2100 / 2500 [ 84%] (Sampling)
Chain 3 Iteration: 2400 / 2500 [ 96%] (Sampling)
Chain 4 Iteration: 2400 / 2500 [ 96%] (Sampling)
Chain 2 Iteration: 2400 / 2500 [ 96%] (Sampling)
Chain 1 Iteration: 2200 / 2500 [ 88%] (Sampling)
Chain 3 Iteration: 2500 / 2500 [100%] (Sampling)
Chain 3 finished in 3419.2 seconds.
Chain 4 Iteration: 2500 / 2500 [100%] (Sampling)
Chain 4 finished in 3435.7 seconds.
Chain 1 Iteration: 2300 / 2500 [ 92%] (Sampling)
Chain 2 Iteration: 2500 / 2500 [100%] (Sampling)
Chain 2 finished in 3494.9 seconds.
Chain 1 Iteration: 2400 / 2500 [ 96%] (Sampling)
Chain 1 Iteration: 2500 / 2500 [100%] (Sampling)
Chain 1 finished in 3614.2 seconds.
All 4 chains finished successfully.
Mean chain execution time: 3491.0 seconds.
Total execution time: 3614.5 seconds.rethinking::precis(m_12h8, depth = 2) mean sd 5.5% 94.5% rhat ess_bulk
kappa[1] -2.543248471 0.110618201 -2.727134400 -2.37322065 1.000564 3200.064
kappa[2] -1.845745451 0.108568338 -2.024542750 -1.67895075 1.000837 3183.619
kappa[3] -1.243801115 0.107624123 -1.422750000 -1.07969560 1.000850 3210.236
kappa[4] -0.185383553 0.107182297 -0.364579740 -0.02155485 1.000868 3173.042
kappa[5] 0.504864538 0.107621735 0.326510305 0.66781222 1.000932 3177.177
kappa[6] 1.431346766 0.108471541 1.251688350 1.59686605 1.000993 3222.315
bG 0.565905856 0.035921202 0.508995050 0.62364011 1.000160 10241.340
bIC -1.264139623 0.095225818 -1.417385500 -1.11486835 1.000797 4694.390
bIAc -0.440852799 0.079535499 -0.568370590 -0.31493810 1.001566 4083.523
bI -0.292420539 0.056825810 -0.382314635 -0.20011494 1.001678 3939.034
b_co -0.343801186 0.068010921 -0.451683695 -0.23348484 1.000499 5042.127
b_ac -0.477491373 0.054401191 -0.564012165 -0.39119847 1.000905 4237.630
bA -0.004687207 0.001553188 -0.007185081 -0.00224420 1.000706 5360.790
bE -0.004746376 0.167020634 -0.277402740 0.24305019 1.001606 2472.784
delta[1] 0.150663091 0.097724954 0.029342110 0.33037780 1.000942 6811.756
delta[2] 0.142494443 0.090471066 0.028268596 0.31099804 1.000341 11536.293
delta[3] 0.138061380 0.090775785 0.028258919 0.31089887 1.000401 7384.363
delta[4] 0.139911480 0.101076463 0.023477432 0.33084020 1.000496 4638.223
delta[5] 0.178860636 0.150356591 0.016438143 0.46561177 1.002125 2610.271
delta[6] 0.120329986 0.080658006 0.023183674 0.27264339 1.000197 7735.726
delta[7] 0.129678980 0.083594897 0.024664563 0.28421408 1.000707 11750.912This model also took forever to sample, over an hour (4229.7 seconds). But now that it finally finished, we can see that the effect of age is similar to wahat it was before, but the effect of education appears to be completely gone. The new effect of gender is definitely positive. So controlling for gender appears to remove the effect of education. If gender is related to education, that can mean that men (the gender coded as 1 in the model) are always more likely to approve of a situation in the trolley problem, and have a different level of educational attainment than women in the study.