set.seed(2384590)
sim_parms <- list(
n = 210,
k = 1.5,
alpha = 2,
beta = -0.35
)
str(sim_parms)List of 4
$ n : num 210
$ k : num 1.5
$ alpha: num 2
$ beta : num -0.35For our previous models, we’ve been concerned about data that have limits of detection, including simultaneous upper and lower limits of detection. For this example, we’ll work through the data generating model for an outcome which is interval censored with a known predictor (extending to a censored predictor follows from this example and the previous examples on censored predictors).
https://www.ncbi.nlm.nih.gov/pmc/articles/PMC3684949/#:~:text=In%20statistical%20literature%2C%20interval%20censoring,instead%20of%20being%20observed%20exactly.
The data generating process for interval censored data I think can be quite variable. Typically I think about this in terms of HAI data, where the observed value is the floored version of the latent value, so a measurement process that generates a value that’s rounded up or down is a data genearting process for an interval censored variable.
The most well-known type of interval censored data comes from studies where the observation time does not completely cover the amount of time where an event could have occurred. For example, consider a factory that runs regularly scheduled maintenance checks, say once per week. If a specific machine fails, but failures are only noticed at the maintenance checks, then we know only that the failure occurred after the last maintenance check and before the current maintenance check. So for example if we report our data weekly, we could say that a particular machine was operational at week 2 and failed by week 3, putting its failure time in the interval \((2, 3]\). (In this example, I consider the interval closed on the upper bound because the machine could have failed moments before the inspection and we would have known it was broken.) Such an example would lead to a data generating process where the failure times are drawn from some random distribution, and then the ceiling is returned by the observation process once the failure times are converted to weeks.
Is there an example of interval censored data generating process that doesn’t come from floor/ceiling of observation process?
One other way to get interval censored data is by responding to a question on a survey which only asks for an interval rather than an exact number.
For this example, we’ll do something different from the usual and model machine failure times. Consider a factory with \(n\) machines. There is redundancy in the amount of available machines to do the factory’s task, and the machines are considered fairly robust, so maintenance checks are performed once a week. For simplicity, we’ll set the parameters such that the expected failure time already has a rate in weeks, so we don’t have to worry about converting the units. If we wanted, e.g., the parameters to be on the scale of days we could probably just rescale the model.
For this model, let’s assume that the rate of failure, \(\lambda_i\) is a linear function of some covariate \(x_i\). I don’t know that much about machines or what would realistically cause them to fail, but we don’t want to make the example too hard at this point, so we want \(x_i\) to be an inherent characteristic of the machine. Let’s say \(x_i\) is some integer number from \(1\) to \(5\) that controls how the machine works – it is inherent to the type of machine. If I can think of a good variable that might work for this, I’ll update that later. The expected failure time increases linearly by some amount \(\beta\) for each unit of increase in \(x_i\). There is also some baseline expected failure rate \(\alpha\) shared by all of the machines. So the expected log failure time (if the failure time were constant) can be given as \[ \log(\lambda_i) = \alpha + \beta x_i. \] We use the log link function here to ensure that expected failure times are always positive, while the function of \(x_i\) does not necessarily need to be.
Finally, we assume that the longer each machine operates without being repaired, the more likely the machine is to fail. We represent this by modeling the failure time as a Weibull distribution with constant parameter \(k\), which influences how quickly the failure rate changes over time. We assume this parameter is the same for all machines, which are identical other than the setting \(x_i\).
So then if our failure times were completely observed, the data generating process would be as follows.
\[ \begin{align*} t^*_i &\sim \mathrm{Weibull}\left(k, \lambda_i\right) \\ \lambda_i &= \alpha + \beta x_i \end{align*} \]
But recall what I said before about running inspections only once a week. If this were the case, assuming our failure times are also measured in weeks, we would also have to apply a censoring mechanism for the data we observe, given by \[t_i = \lceil t_i^* \rceil.\]
We will deal with the interval censoring, as usual, by modifying the likelihood of the outcome. For a completely observed outcome \(t^*_i\), the likelihood would be \[ \mathcal{L}\left(\theta \mid t_i^*\right) = f(t_i^* \mid \theta), \] where \(f(\cdot)\) is the Weibull density function. However, a censored data point actually lies at a point mass of probability and for our censored observation, the contribution to the likelihood is \[ \mathcal{L}\left(\theta \mid t_i\right) = \mathrm{Pr}\left( L_i< t_i \leq U_i \right) = \int_{L_i}^{U_i}f_{T_i}(\tau) \ d\tau = F_{T_i}(U_i) - F_{T_i}(L_i), \] where \(L_i = \lfloor t_i^*\rfloor = t_i - 1\) and \(U_i = \lceil t_i^* \rceil = t_i\), both of which are assumed to be known constants after the data are observed.
The Stan code for this would be {.stan} target += log_diff_exp( weibull_lcdf(y[i] | k, lambda[i]), weibull_lcdf(y[i] - 1 | k, lambda[i]) ) ``` or equivalently target += log_diff_exp( weibull_lcdf(y_u[i] | k, lambda[i]), weibull_lcdf(y_l[i] | k, lambda[i]) )
if the data is specified in the format we prefer. Note that we use the Stan
internal function `log_diff_exp()` for increased numerical precision rather than
dividing the log values of the two functions manually. Note than there are[some
concerns](https://discourse.mc-stan.org/t/interval-censored-data-fails-with-weibull-but-not-gamma/28780)
about the numerical stability of the Weibull CDF function implemented in Stan,
with a [GitHub issue](https://github.com/stan-dev/math/issues/2810) for
improving the stability, open at time of writing. For improved numerical
stability, we can rewrite the `weibull_lcdf()` function using Stan's newer math
functions with improved stability.
````{.stan}
functions {
real my_weibull_lcdf(real y, real alpha, real sigma) {
return log1m_exp(-pow(y / sigma, alpha));
}
}So with the data generating process, including the censoring mechanism, written down, we can simulate some data. As usual, I decided to just plot the data and mess around with the parameters until I thought it looked right.
set.seed(2384590)
sim_parms <- list(
n = 210,
k = 1.5,
alpha = 2,
beta = -0.35
)
str(sim_parms)List of 4
$ n : num 210
$ k : num 1.5
$ alpha: num 2
$ beta : num -0.35gen_data <- function(n, k, alpha, beta) {
out <- tibble::tibble(
x = sample(
1:5, size = n, replace = TRUE,
prob = c(0.4, 0.25, 0.2, 0.1, 0.05)
),
l_lambda = alpha + beta * x,
lambda = exp(l_lambda),
t_star = rweibull(n, shape = k, scale = lambda),
t = ceiling(t_star)
)
return(out)
}
sim_data <- do.call(gen_data, sim_parms)
print(sim_data, n = 5)# A tibble: 210 × 5
x l_lambda lambda t_star t
<int> <dbl> <dbl> <dbl> <dbl>
1 4 0.6 1.82 0.516 1
2 3 0.95 2.59 3.32 4
3 4 0.6 1.82 2.06 3
4 1 1.65 5.21 11.0 11
5 1 1.65 5.21 9.95 10
# ℹ 205 more rowsplot(jitter(sim_data$x), sim_data$t)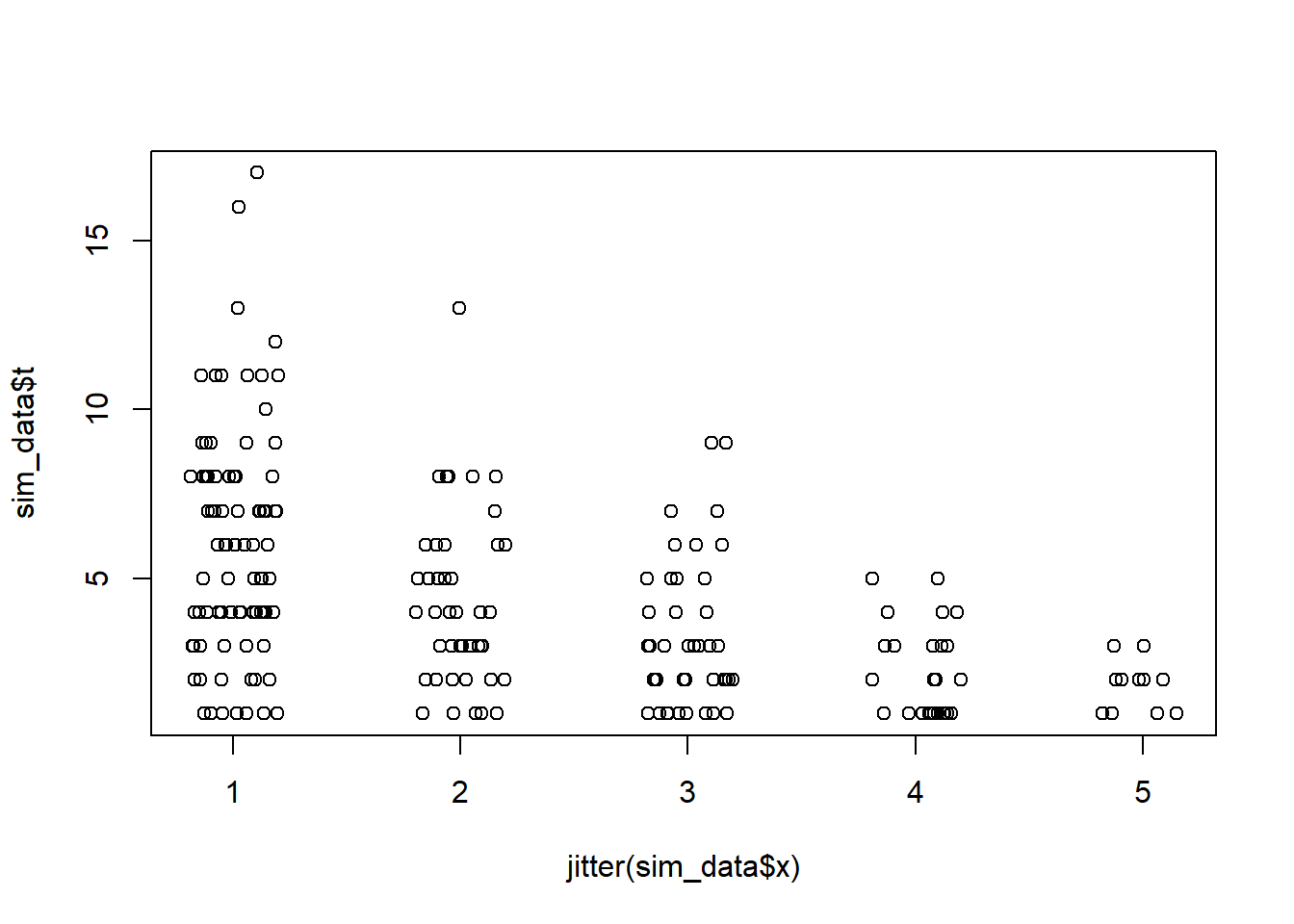
sim_data |> dplyr::group_by(x) |> dplyr::summarise(eft = mean(t))# A tibble: 5 × 2
x eft
<int> <dbl>
1 1 5.82
2 2 4.26
3 3 3.29
4 4 2.19
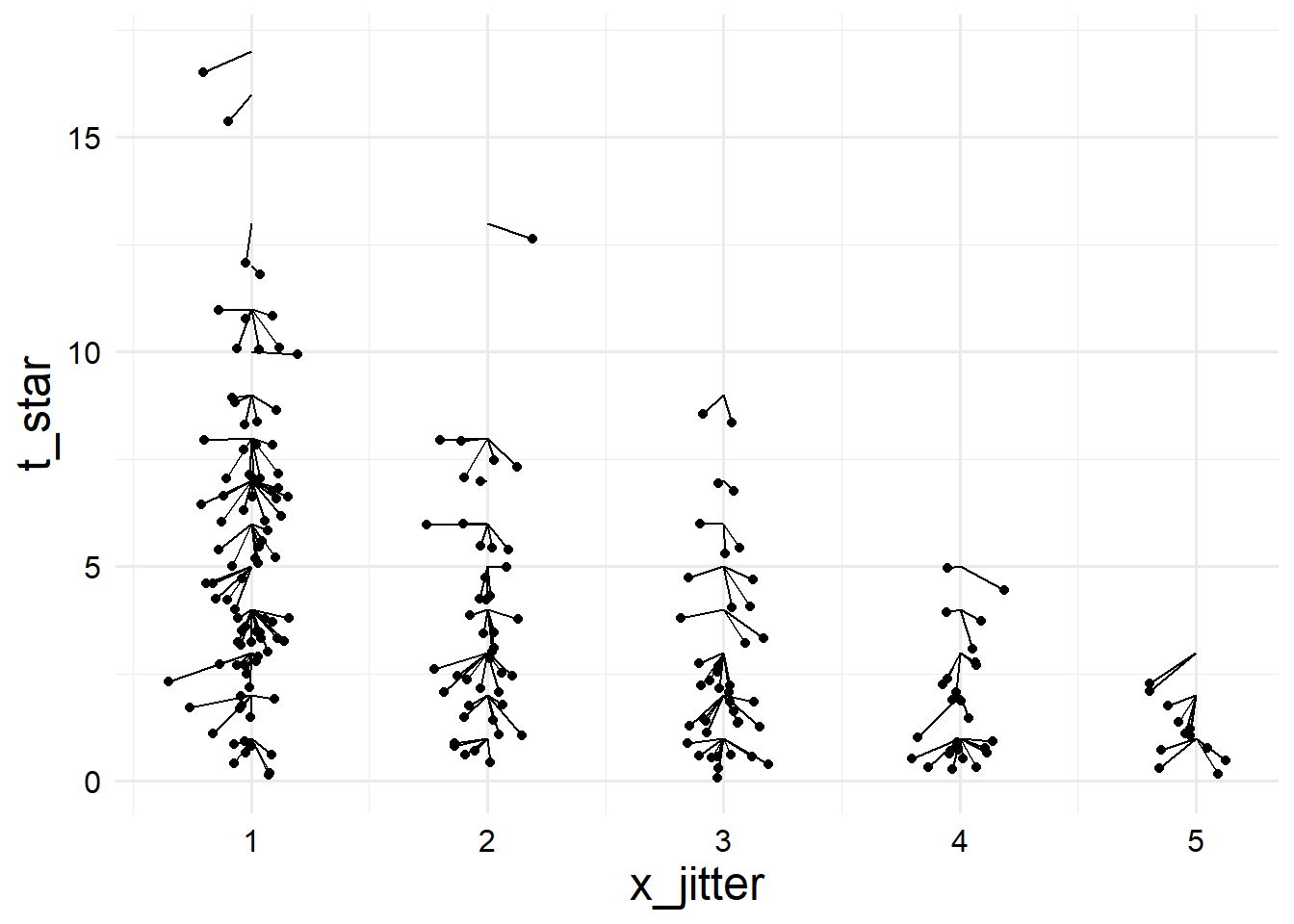
5 5 1.75sim_data |>
dplyr::mutate(
x_jitter = x + rnorm(nrow(sim_data), 0, 0.1)
) |>
ggplot2::ggplot() +
aes(x = x_jitter, y = t_star, group = (x)) +
geom_point() +
geom_segment(
aes(x = x_jitter, xend = x, y = t_star, yend = t)
)
geom_count(shape = 21, fill = "#ffffff50")geom_point: na.rm = FALSE
stat_sum: na.rm = FALSE
position_identity NEED TO LOOK AT HOW BRMS HANDLES INTERVAL CENSORING https://discourse.mc-stan.org/t/mixed-right-left-and-interval-censored-log-normal-with-brms/27571
dat_latent <- list()
dat_latent$N <- nrow(sim_data)
dat_latent$x <- sim_data$x
dat_latent$y <- sim_data$t_star
str(dat_latent)List of 3
$ N: int 210
$ x: int [1:210] 4 3 4 1 1 4 3 1 1 1 ...
$ y: num [1:210] 0.516 3.321 2.061 10.966 9.951 ...mod_pth <- here::here(pth_base, "Ex5a.stan")
mod_l <- cmdstanr::cmdstan_model(mod_pth, compile = FALSE)
mod_l$compile(pedantic = TRUE, force_recompile = TRUE)In file included from stan/lib/stan_math/stan/math/prim/prob/von_mises_lccdf.hpp:5,
from stan/lib/stan_math/stan/math/prim/prob/von_mises_ccdf_log.hpp:4,
from stan/lib/stan_math/stan/math/prim/prob.hpp:356,
from stan/lib/stan_math/stan/math/prim.hpp:16,
from stan/lib/stan_math/stan/math/rev.hpp:14,
from stan/lib/stan_math/stan/math.hpp:19,
from stan/src/stan/model/model_header.hpp:4,
from C:/Users/Zane/AppData/Local/Temp/RtmpkPQFPJ/model-4f1819e036e0.hpp:2:
stan/lib/stan_math/stan/math/prim/prob/von_mises_cdf.hpp: In function 'stan::return_type_t<T_x, T_sigma, T_l> stan::math::von_mises_cdf(const T_x&, const T_mu&, const T_k&)':
stan/lib/stan_math/stan/math/prim/prob/von_mises_cdf.hpp:194: note: '-Wmisleading-indentation' is disabled from this point onwards, since column-tracking was disabled due to the size of the code/headers
194 | if (cdf_n < 0.0)
| stan/lib/stan_math/stan/math/prim/prob/von_mises_cdf.hpp:194: note: adding '-flarge-source-files' will allow for more column-tracking support, at the expense of compilation time and memoryfit_l <- mod_l$sample(
dat_latent,
seed = 546465,
parallel_chains = 4,
iter_warmup = 500,
iter_sampling = 2500,
show_messages = T
)Running MCMC with 4 parallel chains...
Chain 1 Iteration: 1 / 3000 [ 0%] (Warmup)
Chain 1 Iteration: 100 / 3000 [ 3%] (Warmup)
Chain 1 Iteration: 200 / 3000 [ 6%] (Warmup) Chain 1 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:Chain 1 Exception: weibull_lpdf: Shape parameter is 0, but must be positive finite! (in 'C:/Users/Zane/AppData/Local/Temp/RtmpkPQFPJ/model-4f1819e036e0.stan', line 38, column 2 to column 31)Chain 1 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,Chain 1 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.Chain 1 Chain 1 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:Chain 1 Exception: weibull_lpdf: Shape parameter is 0, but must be positive finite! (in 'C:/Users/Zane/AppData/Local/Temp/RtmpkPQFPJ/model-4f1819e036e0.stan', line 38, column 2 to column 31)Chain 1 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,Chain 1 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.Chain 1 Chain 1 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:Chain 1 Exception: weibull_lpdf: Shape parameter is 0, but must be positive finite! (in 'C:/Users/Zane/AppData/Local/Temp/RtmpkPQFPJ/model-4f1819e036e0.stan', line 38, column 2 to column 31)Chain 1 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,Chain 1 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.Chain 1 Chain 1 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:Chain 1 Exception: weibull_lpdf: Shape parameter is 0, but must be positive finite! (in 'C:/Users/Zane/AppData/Local/Temp/RtmpkPQFPJ/model-4f1819e036e0.stan', line 38, column 2 to column 31)Chain 1 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,Chain 1 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.Chain 1 Chain 1 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:Chain 1 Exception: weibull_lpdf: Shape parameter is 0, but must be positive finite! (in 'C:/Users/Zane/AppData/Local/Temp/RtmpkPQFPJ/model-4f1819e036e0.stan', line 38, column 2 to column 31)Chain 1 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,Chain 1 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.Chain 1 Chain 2 Iteration: 1 / 3000 [ 0%] (Warmup)
Chain 2 Iteration: 100 / 3000 [ 3%] (Warmup)
Chain 2 Iteration: 200 / 3000 [ 6%] (Warmup) Chain 2 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:Chain 2 Exception: weibull_lpdf: Shape parameter is 0, but must be positive finite! (in 'C:/Users/Zane/AppData/Local/Temp/RtmpkPQFPJ/model-4f1819e036e0.stan', line 38, column 2 to column 31)Chain 2 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,Chain 2 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.Chain 2 Chain 2 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:Chain 2 Exception: weibull_lpdf: Shape parameter is 0, but must be positive finite! (in 'C:/Users/Zane/AppData/Local/Temp/RtmpkPQFPJ/model-4f1819e036e0.stan', line 38, column 2 to column 31)Chain 2 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,Chain 2 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.Chain 2 Chain 2 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:Chain 2 Exception: weibull_lpdf: Shape parameter is 0, but must be positive finite! (in 'C:/Users/Zane/AppData/Local/Temp/RtmpkPQFPJ/model-4f1819e036e0.stan', line 38, column 2 to column 31)Chain 2 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,Chain 2 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.Chain 2 Chain 2 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:Chain 2 Exception: weibull_lpdf: Shape parameter is 0, but must be positive finite! (in 'C:/Users/Zane/AppData/Local/Temp/RtmpkPQFPJ/model-4f1819e036e0.stan', line 38, column 2 to column 31)Chain 2 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,Chain 2 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.Chain 2 Chain 2 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:Chain 2 Exception: weibull_lpdf: Shape parameter is 0, but must be positive finite! (in 'C:/Users/Zane/AppData/Local/Temp/RtmpkPQFPJ/model-4f1819e036e0.stan', line 38, column 2 to column 31)Chain 2 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,Chain 2 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.Chain 2 Chain 2 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:Chain 2 Exception: weibull_lpdf: Shape parameter is 0, but must be positive finite! (in 'C:/Users/Zane/AppData/Local/Temp/RtmpkPQFPJ/model-4f1819e036e0.stan', line 38, column 2 to column 31)Chain 2 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,Chain 2 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.Chain 2 Chain 2 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:Chain 2 Exception: weibull_lpdf: Shape parameter is 0, but must be positive finite! (in 'C:/Users/Zane/AppData/Local/Temp/RtmpkPQFPJ/model-4f1819e036e0.stan', line 38, column 2 to column 31)Chain 2 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,Chain 2 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.Chain 2 Chain 2 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:Chain 2 Exception: weibull_lpdf: Shape parameter is 0, but must be positive finite! (in 'C:/Users/Zane/AppData/Local/Temp/RtmpkPQFPJ/model-4f1819e036e0.stan', line 38, column 2 to column 31)Chain 2 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,Chain 2 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.Chain 2 Chain 2 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:Chain 2 Exception: weibull_lpdf: Shape parameter is 0, but must be positive finite! (in 'C:/Users/Zane/AppData/Local/Temp/RtmpkPQFPJ/model-4f1819e036e0.stan', line 38, column 2 to column 31)Chain 2 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,Chain 2 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.Chain 2 Chain 2 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:Chain 2 Exception: weibull_lpdf: Shape parameter is 0, but must be positive finite! (in 'C:/Users/Zane/AppData/Local/Temp/RtmpkPQFPJ/model-4f1819e036e0.stan', line 38, column 2 to column 31)Chain 2 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,Chain 2 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.Chain 2 Chain 2 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:Chain 2 Exception: weibull_lpdf: Shape parameter is 0, but must be positive finite! (in 'C:/Users/Zane/AppData/Local/Temp/RtmpkPQFPJ/model-4f1819e036e0.stan', line 38, column 2 to column 31)Chain 2 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,Chain 2 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.Chain 2 Chain 2 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:Chain 2 Exception: weibull_lpdf: Shape parameter is 0, but must be positive finite! (in 'C:/Users/Zane/AppData/Local/Temp/RtmpkPQFPJ/model-4f1819e036e0.stan', line 38, column 2 to column 31)Chain 2 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,Chain 2 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.Chain 2 Chain 2 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:Chain 2 Exception: weibull_lpdf: Shape parameter is 0, but must be positive finite! (in 'C:/Users/Zane/AppData/Local/Temp/RtmpkPQFPJ/model-4f1819e036e0.stan', line 38, column 2 to column 31)Chain 2 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,Chain 2 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.Chain 2 Chain 2 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:Chain 2 Exception: weibull_lpdf: Scale parameter is inf, but must be positive finite! (in 'C:/Users/Zane/AppData/Local/Temp/RtmpkPQFPJ/model-4f1819e036e0.stan', line 38, column 2 to column 31)Chain 2 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,Chain 2 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.Chain 2 Chain 2 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:Chain 2 Exception: weibull_lpdf: Shape parameter is 0, but must be positive finite! (in 'C:/Users/Zane/AppData/Local/Temp/RtmpkPQFPJ/model-4f1819e036e0.stan', line 38, column 2 to column 31)Chain 2 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,Chain 2 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.Chain 2 Chain 2 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:Chain 2 Exception: weibull_lpdf: Shape parameter is 0, but must be positive finite! (in 'C:/Users/Zane/AppData/Local/Temp/RtmpkPQFPJ/model-4f1819e036e0.stan', line 38, column 2 to column 31)Chain 2 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,Chain 2 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.Chain 2 Chain 2 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:Chain 2 Exception: weibull_lpdf: Shape parameter is 0, but must be positive finite! (in 'C:/Users/Zane/AppData/Local/Temp/RtmpkPQFPJ/model-4f1819e036e0.stan', line 38, column 2 to column 31)Chain 2 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,Chain 2 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.Chain 2 Chain 2 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:Chain 2 Exception: weibull_lpdf: Shape parameter is 0, but must be positive finite! (in 'C:/Users/Zane/AppData/Local/Temp/RtmpkPQFPJ/model-4f1819e036e0.stan', line 38, column 2 to column 31)Chain 2 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,Chain 2 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.Chain 2 Chain 2 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:Chain 2 Exception: weibull_lpdf: Shape parameter is 0, but must be positive finite! (in 'C:/Users/Zane/AppData/Local/Temp/RtmpkPQFPJ/model-4f1819e036e0.stan', line 38, column 2 to column 31)Chain 2 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,Chain 2 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.Chain 2 Chain 3 Iteration: 1 / 3000 [ 0%] (Warmup)
Chain 3 Iteration: 100 / 3000 [ 3%] (Warmup) Chain 3 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:Chain 3 Exception: weibull_lpdf: Shape parameter is 0, but must be positive finite! (in 'C:/Users/Zane/AppData/Local/Temp/RtmpkPQFPJ/model-4f1819e036e0.stan', line 38, column 2 to column 31)Chain 3 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,Chain 3 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.Chain 3 Chain 3 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:Chain 3 Exception: weibull_lpdf: Shape parameter is 0, but must be positive finite! (in 'C:/Users/Zane/AppData/Local/Temp/RtmpkPQFPJ/model-4f1819e036e0.stan', line 38, column 2 to column 31)Chain 3 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,Chain 3 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.Chain 3 Chain 3 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:Chain 3 Exception: weibull_lpdf: Shape parameter is 0, but must be positive finite! (in 'C:/Users/Zane/AppData/Local/Temp/RtmpkPQFPJ/model-4f1819e036e0.stan', line 38, column 2 to column 31)Chain 3 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,Chain 3 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.Chain 3 Chain 3 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:Chain 3 Exception: weibull_lpdf: Shape parameter is 0, but must be positive finite! (in 'C:/Users/Zane/AppData/Local/Temp/RtmpkPQFPJ/model-4f1819e036e0.stan', line 38, column 2 to column 31)Chain 3 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,Chain 3 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.Chain 3 Chain 3 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:Chain 3 Exception: weibull_lpdf: Scale parameter is inf, but must be positive finite! (in 'C:/Users/Zane/AppData/Local/Temp/RtmpkPQFPJ/model-4f1819e036e0.stan', line 38, column 2 to column 31)Chain 3 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,Chain 3 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.Chain 3 Chain 3 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:Chain 3 Exception: weibull_lpdf: Shape parameter is 0, but must be positive finite! (in 'C:/Users/Zane/AppData/Local/Temp/RtmpkPQFPJ/model-4f1819e036e0.stan', line 38, column 2 to column 31)Chain 3 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,Chain 3 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.Chain 3 Chain 3 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:Chain 3 Exception: weibull_lpdf: Shape parameter is 0, but must be positive finite! (in 'C:/Users/Zane/AppData/Local/Temp/RtmpkPQFPJ/model-4f1819e036e0.stan', line 38, column 2 to column 31)Chain 3 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,Chain 3 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.Chain 3 Chain 3 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:Chain 3 Exception: weibull_lpdf: Scale parameter is inf, but must be positive finite! (in 'C:/Users/Zane/AppData/Local/Temp/RtmpkPQFPJ/model-4f1819e036e0.stan', line 38, column 2 to column 31)Chain 3 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,Chain 3 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.Chain 3 Chain 4 Iteration: 1 / 3000 [ 0%] (Warmup)
Chain 4 Iteration: 100 / 3000 [ 3%] (Warmup) Chain 4 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:Chain 4 Exception: weibull_lpdf: Shape parameter is 0, but must be positive finite! (in 'C:/Users/Zane/AppData/Local/Temp/RtmpkPQFPJ/model-4f1819e036e0.stan', line 38, column 2 to column 31)Chain 4 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,Chain 4 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.Chain 4 Chain 4 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:Chain 4 Exception: weibull_lpdf: Shape parameter is 0, but must be positive finite! (in 'C:/Users/Zane/AppData/Local/Temp/RtmpkPQFPJ/model-4f1819e036e0.stan', line 38, column 2 to column 31)Chain 4 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,Chain 4 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.Chain 4 Chain 4 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:Chain 4 Exception: weibull_lpdf: Scale parameter is 0, but must be positive finite! (in 'C:/Users/Zane/AppData/Local/Temp/RtmpkPQFPJ/model-4f1819e036e0.stan', line 38, column 2 to column 31)Chain 4 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,Chain 4 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.Chain 4 Chain 4 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:Chain 4 Exception: weibull_lpdf: Shape parameter is 0, but must be positive finite! (in 'C:/Users/Zane/AppData/Local/Temp/RtmpkPQFPJ/model-4f1819e036e0.stan', line 38, column 2 to column 31)Chain 4 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,Chain 4 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.Chain 4 Chain 4 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:Chain 4 Exception: weibull_lpdf: Scale parameter is 0, but must be positive finite! (in 'C:/Users/Zane/AppData/Local/Temp/RtmpkPQFPJ/model-4f1819e036e0.stan', line 38, column 2 to column 31)Chain 4 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,Chain 4 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.Chain 4 Chain 1 Iteration: 300 / 3000 [ 10%] (Warmup)
Chain 1 Iteration: 400 / 3000 [ 13%] (Warmup)
Chain 1 Iteration: 500 / 3000 [ 16%] (Warmup)
Chain 1 Iteration: 501 / 3000 [ 16%] (Sampling)
Chain 1 Iteration: 600 / 3000 [ 20%] (Sampling)
Chain 1 Iteration: 700 / 3000 [ 23%] (Sampling)
Chain 1 Iteration: 800 / 3000 [ 26%] (Sampling)
Chain 1 Iteration: 900 / 3000 [ 30%] (Sampling)
Chain 2 Iteration: 300 / 3000 [ 10%] (Warmup)
Chain 2 Iteration: 400 / 3000 [ 13%] (Warmup)
Chain 2 Iteration: 500 / 3000 [ 16%] (Warmup)
Chain 2 Iteration: 501 / 3000 [ 16%] (Sampling)
Chain 2 Iteration: 600 / 3000 [ 20%] (Sampling)
Chain 2 Iteration: 700 / 3000 [ 23%] (Sampling)
Chain 2 Iteration: 800 / 3000 [ 26%] (Sampling)
Chain 3 Iteration: 200 / 3000 [ 6%] (Warmup)
Chain 3 Iteration: 300 / 3000 [ 10%] (Warmup)
Chain 3 Iteration: 400 / 3000 [ 13%] (Warmup)
Chain 3 Iteration: 500 / 3000 [ 16%] (Warmup)
Chain 3 Iteration: 501 / 3000 [ 16%] (Sampling)
Chain 3 Iteration: 600 / 3000 [ 20%] (Sampling)
Chain 3 Iteration: 700 / 3000 [ 23%] (Sampling)
Chain 3 Iteration: 800 / 3000 [ 26%] (Sampling)
Chain 3 Iteration: 900 / 3000 [ 30%] (Sampling)
Chain 4 Iteration: 200 / 3000 [ 6%] (Warmup)
Chain 4 Iteration: 300 / 3000 [ 10%] (Warmup)
Chain 4 Iteration: 400 / 3000 [ 13%] (Warmup)
Chain 4 Iteration: 500 / 3000 [ 16%] (Warmup)
Chain 4 Iteration: 501 / 3000 [ 16%] (Sampling)
Chain 4 Iteration: 600 / 3000 [ 20%] (Sampling)
Chain 4 Iteration: 700 / 3000 [ 23%] (Sampling)
Chain 1 Iteration: 1000 / 3000 [ 33%] (Sampling)
Chain 1 Iteration: 1100 / 3000 [ 36%] (Sampling)
Chain 1 Iteration: 1200 / 3000 [ 40%] (Sampling)
Chain 2 Iteration: 900 / 3000 [ 30%] (Sampling)
Chain 2 Iteration: 1000 / 3000 [ 33%] (Sampling)
Chain 2 Iteration: 1100 / 3000 [ 36%] (Sampling)
Chain 3 Iteration: 1000 / 3000 [ 33%] (Sampling)
Chain 3 Iteration: 1100 / 3000 [ 36%] (Sampling)
Chain 3 Iteration: 1200 / 3000 [ 40%] (Sampling)
Chain 4 Iteration: 800 / 3000 [ 26%] (Sampling)
Chain 4 Iteration: 900 / 3000 [ 30%] (Sampling)
Chain 4 Iteration: 1000 / 3000 [ 33%] (Sampling)
Chain 1 Iteration: 1300 / 3000 [ 43%] (Sampling)
Chain 1 Iteration: 1400 / 3000 [ 46%] (Sampling)
Chain 1 Iteration: 1500 / 3000 [ 50%] (Sampling)
Chain 2 Iteration: 1200 / 3000 [ 40%] (Sampling)
Chain 2 Iteration: 1300 / 3000 [ 43%] (Sampling)
Chain 3 Iteration: 1300 / 3000 [ 43%] (Sampling)
Chain 3 Iteration: 1400 / 3000 [ 46%] (Sampling)
Chain 3 Iteration: 1500 / 3000 [ 50%] (Sampling)
Chain 4 Iteration: 1100 / 3000 [ 36%] (Sampling)
Chain 4 Iteration: 1200 / 3000 [ 40%] (Sampling)
Chain 1 Iteration: 1600 / 3000 [ 53%] (Sampling)
Chain 1 Iteration: 1700 / 3000 [ 56%] (Sampling)
Chain 2 Iteration: 1400 / 3000 [ 46%] (Sampling)
Chain 2 Iteration: 1500 / 3000 [ 50%] (Sampling)
Chain 2 Iteration: 1600 / 3000 [ 53%] (Sampling)
Chain 3 Iteration: 1600 / 3000 [ 53%] (Sampling)
Chain 3 Iteration: 1700 / 3000 [ 56%] (Sampling)
Chain 3 Iteration: 1800 / 3000 [ 60%] (Sampling)
Chain 4 Iteration: 1300 / 3000 [ 43%] (Sampling)
Chain 4 Iteration: 1400 / 3000 [ 46%] (Sampling)
Chain 4 Iteration: 1500 / 3000 [ 50%] (Sampling)
Chain 1 Iteration: 1800 / 3000 [ 60%] (Sampling)
Chain 1 Iteration: 1900 / 3000 [ 63%] (Sampling)
Chain 1 Iteration: 2000 / 3000 [ 66%] (Sampling)
Chain 2 Iteration: 1700 / 3000 [ 56%] (Sampling)
Chain 2 Iteration: 1800 / 3000 [ 60%] (Sampling)
Chain 3 Iteration: 1900 / 3000 [ 63%] (Sampling)
Chain 3 Iteration: 2000 / 3000 [ 66%] (Sampling)
Chain 4 Iteration: 1600 / 3000 [ 53%] (Sampling)
Chain 4 Iteration: 1700 / 3000 [ 56%] (Sampling)
Chain 1 Iteration: 2100 / 3000 [ 70%] (Sampling)
Chain 1 Iteration: 2200 / 3000 [ 73%] (Sampling)
Chain 2 Iteration: 1900 / 3000 [ 63%] (Sampling)
Chain 2 Iteration: 2000 / 3000 [ 66%] (Sampling)
Chain 3 Iteration: 2100 / 3000 [ 70%] (Sampling)
Chain 3 Iteration: 2200 / 3000 [ 73%] (Sampling)
Chain 3 Iteration: 2300 / 3000 [ 76%] (Sampling)
Chain 4 Iteration: 1800 / 3000 [ 60%] (Sampling)
Chain 4 Iteration: 1900 / 3000 [ 63%] (Sampling)
Chain 1 Iteration: 2300 / 3000 [ 76%] (Sampling)
Chain 1 Iteration: 2400 / 3000 [ 80%] (Sampling)
Chain 1 Iteration: 2500 / 3000 [ 83%] (Sampling)
Chain 2 Iteration: 2100 / 3000 [ 70%] (Sampling)
Chain 2 Iteration: 2200 / 3000 [ 73%] (Sampling)
Chain 3 Iteration: 2400 / 3000 [ 80%] (Sampling)
Chain 3 Iteration: 2500 / 3000 [ 83%] (Sampling)
Chain 3 Iteration: 2600 / 3000 [ 86%] (Sampling)
Chain 4 Iteration: 2000 / 3000 [ 66%] (Sampling)
Chain 4 Iteration: 2100 / 3000 [ 70%] (Sampling)
Chain 1 Iteration: 2600 / 3000 [ 86%] (Sampling)
Chain 1 Iteration: 2700 / 3000 [ 90%] (Sampling)
Chain 2 Iteration: 2300 / 3000 [ 76%] (Sampling)
Chain 2 Iteration: 2400 / 3000 [ 80%] (Sampling)
Chain 2 Iteration: 2500 / 3000 [ 83%] (Sampling)
Chain 3 Iteration: 2700 / 3000 [ 90%] (Sampling)
Chain 3 Iteration: 2800 / 3000 [ 93%] (Sampling)
Chain 4 Iteration: 2200 / 3000 [ 73%] (Sampling)
Chain 4 Iteration: 2300 / 3000 [ 76%] (Sampling)
Chain 1 Iteration: 2800 / 3000 [ 93%] (Sampling)
Chain 1 Iteration: 2900 / 3000 [ 96%] (Sampling)
Chain 1 Iteration: 3000 / 3000 [100%] (Sampling)
Chain 2 Iteration: 2600 / 3000 [ 86%] (Sampling)
Chain 2 Iteration: 2700 / 3000 [ 90%] (Sampling)
Chain 3 Iteration: 2900 / 3000 [ 96%] (Sampling)
Chain 3 Iteration: 3000 / 3000 [100%] (Sampling)
Chain 4 Iteration: 2400 / 3000 [ 80%] (Sampling)
Chain 4 Iteration: 2500 / 3000 [ 83%] (Sampling)
Chain 1 finished in 1.3 seconds.
Chain 3 finished in 1.3 seconds.
Chain 2 Iteration: 2800 / 3000 [ 93%] (Sampling)
Chain 2 Iteration: 2900 / 3000 [ 96%] (Sampling)
Chain 4 Iteration: 2600 / 3000 [ 86%] (Sampling)
Chain 4 Iteration: 2700 / 3000 [ 90%] (Sampling)
Chain 4 Iteration: 2800 / 3000 [ 93%] (Sampling)
Chain 2 Iteration: 3000 / 3000 [100%] (Sampling)
Chain 4 Iteration: 2900 / 3000 [ 96%] (Sampling)
Chain 4 Iteration: 3000 / 3000 [100%] (Sampling)
Chain 2 finished in 1.5 seconds.
Chain 4 finished in 1.5 seconds.
All 4 chains finished successfully.
Mean chain execution time: 1.4 seconds.
Total execution time: 1.7 seconds.fit_l$summary()# A tibble: 4 × 10
variable mean median sd mad q5 q95 rhat ess_bulk
<chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 lp__ -453. -453. 1.21 0.970 -456. -452. 1.00 4128.
2 alpha 2.14 2.14 0.0997 0.101 1.98 2.30 1.00 3284.
3 beta -0.360 -0.360 0.0392 0.0396 -0.424 -0.296 1.00 3247.
4 k 1.45 1.45 0.0782 0.0786 1.32 1.58 1.00 6020.
# ℹ 1 more variable: ess_tail <dbl>dat_naive <- dat_latent
dat_naive$y <- sim_data$t
str(dat_naive)List of 3
$ N: int 210
$ x: int [1:210] 4 3 4 1 1 4 3 1 1 1 ...
$ y: num [1:210] 1 4 3 11 10 1 3 4 2 4 ...fit_n <- mod_l$sample(
dat_naive,
seed = 546465,
parallel_chains = 4,
iter_warmup = 500,
iter_sampling = 2500,
show_messages = T
)Running MCMC with 4 parallel chains...
Chain 1 Iteration: 1 / 3000 [ 0%] (Warmup)
Chain 1 Iteration: 100 / 3000 [ 3%] (Warmup)
Chain 1 Iteration: 200 / 3000 [ 6%] (Warmup) Chain 1 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:Chain 1 Exception: weibull_lpdf: Shape parameter is 0, but must be positive finite! (in 'C:/Users/Zane/AppData/Local/Temp/RtmpkPQFPJ/model-4f1819e036e0.stan', line 38, column 2 to column 31)Chain 1 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,Chain 1 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.Chain 1 Chain 1 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:Chain 1 Exception: weibull_lpdf: Shape parameter is 0, but must be positive finite! (in 'C:/Users/Zane/AppData/Local/Temp/RtmpkPQFPJ/model-4f1819e036e0.stan', line 38, column 2 to column 31)Chain 1 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,Chain 1 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.Chain 1 Chain 1 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:Chain 1 Exception: weibull_lpdf: Shape parameter is 0, but must be positive finite! (in 'C:/Users/Zane/AppData/Local/Temp/RtmpkPQFPJ/model-4f1819e036e0.stan', line 38, column 2 to column 31)Chain 1 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,Chain 1 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.Chain 1 Chain 1 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:Chain 1 Exception: weibull_lpdf: Scale parameter is inf, but must be positive finite! (in 'C:/Users/Zane/AppData/Local/Temp/RtmpkPQFPJ/model-4f1819e036e0.stan', line 38, column 2 to column 31)Chain 1 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,Chain 1 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.Chain 1 Chain 1 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:Chain 1 Exception: weibull_lpdf: Shape parameter is 0, but must be positive finite! (in 'C:/Users/Zane/AppData/Local/Temp/RtmpkPQFPJ/model-4f1819e036e0.stan', line 38, column 2 to column 31)Chain 1 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,Chain 1 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.Chain 1 Chain 1 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:Chain 1 Exception: weibull_lpdf: Shape parameter is 0, but must be positive finite! (in 'C:/Users/Zane/AppData/Local/Temp/RtmpkPQFPJ/model-4f1819e036e0.stan', line 38, column 2 to column 31)Chain 1 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,Chain 1 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.Chain 1 Chain 2 Iteration: 1 / 3000 [ 0%] (Warmup)
Chain 2 Iteration: 100 / 3000 [ 3%] (Warmup)
Chain 2 Iteration: 200 / 3000 [ 6%] (Warmup) Chain 2 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:Chain 2 Exception: weibull_lpdf: Shape parameter is 0, but must be positive finite! (in 'C:/Users/Zane/AppData/Local/Temp/RtmpkPQFPJ/model-4f1819e036e0.stan', line 38, column 2 to column 31)Chain 2 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,Chain 2 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.Chain 2 Chain 2 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:Chain 2 Exception: weibull_lpdf: Shape parameter is 0, but must be positive finite! (in 'C:/Users/Zane/AppData/Local/Temp/RtmpkPQFPJ/model-4f1819e036e0.stan', line 38, column 2 to column 31)Chain 2 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,Chain 2 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.Chain 2 Chain 2 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:Chain 2 Exception: weibull_lpdf: Shape parameter is 0, but must be positive finite! (in 'C:/Users/Zane/AppData/Local/Temp/RtmpkPQFPJ/model-4f1819e036e0.stan', line 38, column 2 to column 31)Chain 2 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,Chain 2 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.Chain 2 Chain 2 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:Chain 2 Exception: weibull_lpdf: Shape parameter is 0, but must be positive finite! (in 'C:/Users/Zane/AppData/Local/Temp/RtmpkPQFPJ/model-4f1819e036e0.stan', line 38, column 2 to column 31)Chain 2 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,Chain 2 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.Chain 2 Chain 2 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:Chain 2 Exception: weibull_lpdf: Shape parameter is 0, but must be positive finite! (in 'C:/Users/Zane/AppData/Local/Temp/RtmpkPQFPJ/model-4f1819e036e0.stan', line 38, column 2 to column 31)Chain 2 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,Chain 2 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.Chain 2 Chain 2 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:Chain 2 Exception: weibull_lpdf: Shape parameter is 0, but must be positive finite! (in 'C:/Users/Zane/AppData/Local/Temp/RtmpkPQFPJ/model-4f1819e036e0.stan', line 38, column 2 to column 31)Chain 2 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,Chain 2 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.Chain 2 Chain 2 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:Chain 2 Exception: weibull_lpdf: Shape parameter is 0, but must be positive finite! (in 'C:/Users/Zane/AppData/Local/Temp/RtmpkPQFPJ/model-4f1819e036e0.stan', line 38, column 2 to column 31)Chain 2 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,Chain 2 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.Chain 2 Chain 2 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:Chain 2 Exception: weibull_lpdf: Shape parameter is 0, but must be positive finite! (in 'C:/Users/Zane/AppData/Local/Temp/RtmpkPQFPJ/model-4f1819e036e0.stan', line 38, column 2 to column 31)Chain 2 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,Chain 2 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.Chain 2 Chain 2 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:Chain 2 Exception: weibull_lpdf: Shape parameter is 0, but must be positive finite! (in 'C:/Users/Zane/AppData/Local/Temp/RtmpkPQFPJ/model-4f1819e036e0.stan', line 38, column 2 to column 31)Chain 2 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,Chain 2 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.Chain 2 Chain 2 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:Chain 2 Exception: weibull_lpdf: Shape parameter is 0, but must be positive finite! (in 'C:/Users/Zane/AppData/Local/Temp/RtmpkPQFPJ/model-4f1819e036e0.stan', line 38, column 2 to column 31)Chain 2 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,Chain 2 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.Chain 2 Chain 2 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:Chain 2 Exception: weibull_lpdf: Shape parameter is 0, but must be positive finite! (in 'C:/Users/Zane/AppData/Local/Temp/RtmpkPQFPJ/model-4f1819e036e0.stan', line 38, column 2 to column 31)Chain 2 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,Chain 2 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.Chain 2 Chain 2 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:Chain 2 Exception: weibull_lpdf: Shape parameter is 0, but must be positive finite! (in 'C:/Users/Zane/AppData/Local/Temp/RtmpkPQFPJ/model-4f1819e036e0.stan', line 38, column 2 to column 31)Chain 2 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,Chain 2 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.Chain 2 Chain 2 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:Chain 2 Exception: weibull_lpdf: Shape parameter is 0, but must be positive finite! (in 'C:/Users/Zane/AppData/Local/Temp/RtmpkPQFPJ/model-4f1819e036e0.stan', line 38, column 2 to column 31)Chain 2 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,Chain 2 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.Chain 2 Chain 2 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:Chain 2 Exception: weibull_lpdf: Scale parameter is inf, but must be positive finite! (in 'C:/Users/Zane/AppData/Local/Temp/RtmpkPQFPJ/model-4f1819e036e0.stan', line 38, column 2 to column 31)Chain 2 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,Chain 2 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.Chain 2 Chain 2 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:Chain 2 Exception: weibull_lpdf: Shape parameter is 0, but must be positive finite! (in 'C:/Users/Zane/AppData/Local/Temp/RtmpkPQFPJ/model-4f1819e036e0.stan', line 38, column 2 to column 31)Chain 2 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,Chain 2 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.Chain 2 Chain 2 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:Chain 2 Exception: weibull_lpdf: Shape parameter is 0, but must be positive finite! (in 'C:/Users/Zane/AppData/Local/Temp/RtmpkPQFPJ/model-4f1819e036e0.stan', line 38, column 2 to column 31)Chain 2 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,Chain 2 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.Chain 2 Chain 2 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:Chain 2 Exception: weibull_lpdf: Shape parameter is 0, but must be positive finite! (in 'C:/Users/Zane/AppData/Local/Temp/RtmpkPQFPJ/model-4f1819e036e0.stan', line 38, column 2 to column 31)Chain 2 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,Chain 2 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.Chain 2 Chain 2 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:Chain 2 Exception: weibull_lpdf: Shape parameter is 0, but must be positive finite! (in 'C:/Users/Zane/AppData/Local/Temp/RtmpkPQFPJ/model-4f1819e036e0.stan', line 38, column 2 to column 31)Chain 2 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,Chain 2 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.Chain 2 Chain 2 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:Chain 2 Exception: weibull_lpdf: Shape parameter is 0, but must be positive finite! (in 'C:/Users/Zane/AppData/Local/Temp/RtmpkPQFPJ/model-4f1819e036e0.stan', line 38, column 2 to column 31)Chain 2 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,Chain 2 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.Chain 2 Chain 3 Iteration: 1 / 3000 [ 0%] (Warmup)
Chain 3 Iteration: 100 / 3000 [ 3%] (Warmup) Chain 3 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:Chain 3 Exception: weibull_lpdf: Shape parameter is 0, but must be positive finite! (in 'C:/Users/Zane/AppData/Local/Temp/RtmpkPQFPJ/model-4f1819e036e0.stan', line 38, column 2 to column 31)Chain 3 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,Chain 3 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.Chain 3 Chain 3 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:Chain 3 Exception: weibull_lpdf: Shape parameter is 0, but must be positive finite! (in 'C:/Users/Zane/AppData/Local/Temp/RtmpkPQFPJ/model-4f1819e036e0.stan', line 38, column 2 to column 31)Chain 3 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,Chain 3 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.Chain 3 Chain 3 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:Chain 3 Exception: weibull_lpdf: Shape parameter is 0, but must be positive finite! (in 'C:/Users/Zane/AppData/Local/Temp/RtmpkPQFPJ/model-4f1819e036e0.stan', line 38, column 2 to column 31)Chain 3 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,Chain 3 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.Chain 3 Chain 3 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:Chain 3 Exception: weibull_lpdf: Shape parameter is 0, but must be positive finite! (in 'C:/Users/Zane/AppData/Local/Temp/RtmpkPQFPJ/model-4f1819e036e0.stan', line 38, column 2 to column 31)Chain 3 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,Chain 3 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.Chain 3 Chain 3 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:Chain 3 Exception: weibull_lpdf: Scale parameter is inf, but must be positive finite! (in 'C:/Users/Zane/AppData/Local/Temp/RtmpkPQFPJ/model-4f1819e036e0.stan', line 38, column 2 to column 31)Chain 3 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,Chain 3 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.Chain 3 Chain 3 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:Chain 3 Exception: weibull_lpdf: Shape parameter is 0, but must be positive finite! (in 'C:/Users/Zane/AppData/Local/Temp/RtmpkPQFPJ/model-4f1819e036e0.stan', line 38, column 2 to column 31)Chain 3 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,Chain 3 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.Chain 3 Chain 3 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:Chain 3 Exception: weibull_lpdf: Shape parameter is 0, but must be positive finite! (in 'C:/Users/Zane/AppData/Local/Temp/RtmpkPQFPJ/model-4f1819e036e0.stan', line 38, column 2 to column 31)Chain 3 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,Chain 3 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.Chain 3 Chain 3 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:Chain 3 Exception: weibull_lpdf: Scale parameter is inf, but must be positive finite! (in 'C:/Users/Zane/AppData/Local/Temp/RtmpkPQFPJ/model-4f1819e036e0.stan', line 38, column 2 to column 31)Chain 3 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,Chain 3 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.Chain 3 Chain 4 Iteration: 1 / 3000 [ 0%] (Warmup)
Chain 4 Iteration: 100 / 3000 [ 3%] (Warmup)
Chain 4 Iteration: 200 / 3000 [ 6%] (Warmup) Chain 4 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:Chain 4 Exception: weibull_lpdf: Shape parameter is 0, but must be positive finite! (in 'C:/Users/Zane/AppData/Local/Temp/RtmpkPQFPJ/model-4f1819e036e0.stan', line 38, column 2 to column 31)Chain 4 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,Chain 4 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.Chain 4 Chain 4 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:Chain 4 Exception: weibull_lpdf: Shape parameter is 0, but must be positive finite! (in 'C:/Users/Zane/AppData/Local/Temp/RtmpkPQFPJ/model-4f1819e036e0.stan', line 38, column 2 to column 31)Chain 4 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,Chain 4 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.Chain 4 Chain 4 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:Chain 4 Exception: weibull_lpdf: Scale parameter is 0, but must be positive finite! (in 'C:/Users/Zane/AppData/Local/Temp/RtmpkPQFPJ/model-4f1819e036e0.stan', line 38, column 2 to column 31)Chain 4 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,Chain 4 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.Chain 4 Chain 4 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:Chain 4 Exception: weibull_lpdf: Shape parameter is 0, but must be positive finite! (in 'C:/Users/Zane/AppData/Local/Temp/RtmpkPQFPJ/model-4f1819e036e0.stan', line 38, column 2 to column 31)Chain 4 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,Chain 4 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.Chain 4 Chain 4 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:Chain 4 Exception: weibull_lpdf: Scale parameter is 0, but must be positive finite! (in 'C:/Users/Zane/AppData/Local/Temp/RtmpkPQFPJ/model-4f1819e036e0.stan', line 38, column 2 to column 31)Chain 4 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,Chain 4 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.Chain 4 Chain 1 Iteration: 300 / 3000 [ 10%] (Warmup)
Chain 1 Iteration: 400 / 3000 [ 13%] (Warmup)
Chain 1 Iteration: 500 / 3000 [ 16%] (Warmup)
Chain 1 Iteration: 501 / 3000 [ 16%] (Sampling)
Chain 1 Iteration: 600 / 3000 [ 20%] (Sampling)
Chain 1 Iteration: 700 / 3000 [ 23%] (Sampling)
Chain 2 Iteration: 300 / 3000 [ 10%] (Warmup)
Chain 2 Iteration: 400 / 3000 [ 13%] (Warmup)
Chain 2 Iteration: 500 / 3000 [ 16%] (Warmup)
Chain 2 Iteration: 501 / 3000 [ 16%] (Sampling)
Chain 2 Iteration: 600 / 3000 [ 20%] (Sampling)
Chain 2 Iteration: 700 / 3000 [ 23%] (Sampling)
Chain 3 Iteration: 200 / 3000 [ 6%] (Warmup)
Chain 3 Iteration: 300 / 3000 [ 10%] (Warmup)
Chain 3 Iteration: 400 / 3000 [ 13%] (Warmup)
Chain 3 Iteration: 500 / 3000 [ 16%] (Warmup)
Chain 3 Iteration: 501 / 3000 [ 16%] (Sampling)
Chain 3 Iteration: 600 / 3000 [ 20%] (Sampling)
Chain 3 Iteration: 700 / 3000 [ 23%] (Sampling)
Chain 3 Iteration: 800 / 3000 [ 26%] (Sampling)
Chain 4 Iteration: 300 / 3000 [ 10%] (Warmup)
Chain 4 Iteration: 400 / 3000 [ 13%] (Warmup)
Chain 4 Iteration: 500 / 3000 [ 16%] (Warmup)
Chain 4 Iteration: 501 / 3000 [ 16%] (Sampling)
Chain 4 Iteration: 600 / 3000 [ 20%] (Sampling)
Chain 4 Iteration: 700 / 3000 [ 23%] (Sampling)
Chain 4 Iteration: 800 / 3000 [ 26%] (Sampling)
Chain 1 Iteration: 800 / 3000 [ 26%] (Sampling)
Chain 1 Iteration: 900 / 3000 [ 30%] (Sampling)
Chain 1 Iteration: 1000 / 3000 [ 33%] (Sampling)
Chain 2 Iteration: 800 / 3000 [ 26%] (Sampling)
Chain 2 Iteration: 900 / 3000 [ 30%] (Sampling)
Chain 2 Iteration: 1000 / 3000 [ 33%] (Sampling)
Chain 3 Iteration: 900 / 3000 [ 30%] (Sampling)
Chain 3 Iteration: 1000 / 3000 [ 33%] (Sampling)
Chain 4 Iteration: 900 / 3000 [ 30%] (Sampling)
Chain 4 Iteration: 1000 / 3000 [ 33%] (Sampling)
Chain 1 Iteration: 1100 / 3000 [ 36%] (Sampling)
Chain 1 Iteration: 1200 / 3000 [ 40%] (Sampling)
Chain 2 Iteration: 1100 / 3000 [ 36%] (Sampling)
Chain 2 Iteration: 1200 / 3000 [ 40%] (Sampling)
Chain 3 Iteration: 1100 / 3000 [ 36%] (Sampling)
Chain 3 Iteration: 1200 / 3000 [ 40%] (Sampling)
Chain 4 Iteration: 1100 / 3000 [ 36%] (Sampling)
Chain 4 Iteration: 1200 / 3000 [ 40%] (Sampling)
Chain 4 Iteration: 1300 / 3000 [ 43%] (Sampling)
Chain 1 Iteration: 1300 / 3000 [ 43%] (Sampling)
Chain 1 Iteration: 1400 / 3000 [ 46%] (Sampling)
Chain 2 Iteration: 1300 / 3000 [ 43%] (Sampling)
Chain 2 Iteration: 1400 / 3000 [ 46%] (Sampling)
Chain 3 Iteration: 1300 / 3000 [ 43%] (Sampling)
Chain 3 Iteration: 1400 / 3000 [ 46%] (Sampling)
Chain 4 Iteration: 1400 / 3000 [ 46%] (Sampling)
Chain 4 Iteration: 1500 / 3000 [ 50%] (Sampling)
Chain 1 Iteration: 1500 / 3000 [ 50%] (Sampling)
Chain 1 Iteration: 1600 / 3000 [ 53%] (Sampling)
Chain 2 Iteration: 1500 / 3000 [ 50%] (Sampling)
Chain 2 Iteration: 1600 / 3000 [ 53%] (Sampling)
Chain 3 Iteration: 1500 / 3000 [ 50%] (Sampling)
Chain 3 Iteration: 1600 / 3000 [ 53%] (Sampling)
Chain 4 Iteration: 1600 / 3000 [ 53%] (Sampling)
Chain 4 Iteration: 1700 / 3000 [ 56%] (Sampling)
Chain 4 Iteration: 1800 / 3000 [ 60%] (Sampling)
Chain 1 Iteration: 1700 / 3000 [ 56%] (Sampling)
Chain 1 Iteration: 1800 / 3000 [ 60%] (Sampling)
Chain 2 Iteration: 1700 / 3000 [ 56%] (Sampling)
Chain 2 Iteration: 1800 / 3000 [ 60%] (Sampling)
Chain 3 Iteration: 1700 / 3000 [ 56%] (Sampling)
Chain 3 Iteration: 1800 / 3000 [ 60%] (Sampling)
Chain 4 Iteration: 1900 / 3000 [ 63%] (Sampling)
Chain 4 Iteration: 2000 / 3000 [ 66%] (Sampling)
Chain 1 Iteration: 1900 / 3000 [ 63%] (Sampling)
Chain 1 Iteration: 2000 / 3000 [ 66%] (Sampling)
Chain 2 Iteration: 1900 / 3000 [ 63%] (Sampling)
Chain 2 Iteration: 2000 / 3000 [ 66%] (Sampling)
Chain 3 Iteration: 1900 / 3000 [ 63%] (Sampling)
Chain 3 Iteration: 2000 / 3000 [ 66%] (Sampling)
Chain 3 Iteration: 2100 / 3000 [ 70%] (Sampling)
Chain 4 Iteration: 2100 / 3000 [ 70%] (Sampling)
Chain 4 Iteration: 2200 / 3000 [ 73%] (Sampling)
Chain 4 Iteration: 2300 / 3000 [ 76%] (Sampling)
Chain 1 Iteration: 2100 / 3000 [ 70%] (Sampling)
Chain 1 Iteration: 2200 / 3000 [ 73%] (Sampling)
Chain 2 Iteration: 2100 / 3000 [ 70%] (Sampling)
Chain 2 Iteration: 2200 / 3000 [ 73%] (Sampling)
Chain 3 Iteration: 2200 / 3000 [ 73%] (Sampling)
Chain 4 Iteration: 2400 / 3000 [ 80%] (Sampling)
Chain 4 Iteration: 2500 / 3000 [ 83%] (Sampling)
Chain 1 Iteration: 2300 / 3000 [ 76%] (Sampling)
Chain 1 Iteration: 2400 / 3000 [ 80%] (Sampling)
Chain 2 Iteration: 2300 / 3000 [ 76%] (Sampling)
Chain 3 Iteration: 2300 / 3000 [ 76%] (Sampling)
Chain 3 Iteration: 2400 / 3000 [ 80%] (Sampling)
Chain 4 Iteration: 2600 / 3000 [ 86%] (Sampling)
Chain 1 Iteration: 2500 / 3000 [ 83%] (Sampling)
Chain 1 Iteration: 2600 / 3000 [ 86%] (Sampling)
Chain 2 Iteration: 2400 / 3000 [ 80%] (Sampling)
Chain 2 Iteration: 2500 / 3000 [ 83%] (Sampling)
Chain 3 Iteration: 2500 / 3000 [ 83%] (Sampling)
Chain 3 Iteration: 2600 / 3000 [ 86%] (Sampling)
Chain 4 Iteration: 2700 / 3000 [ 90%] (Sampling)
Chain 4 Iteration: 2800 / 3000 [ 93%] (Sampling)
Chain 4 Iteration: 2900 / 3000 [ 96%] (Sampling)
Chain 1 Iteration: 2700 / 3000 [ 90%] (Sampling)
Chain 1 Iteration: 2800 / 3000 [ 93%] (Sampling)
Chain 2 Iteration: 2600 / 3000 [ 86%] (Sampling)
Chain 2 Iteration: 2700 / 3000 [ 90%] (Sampling)
Chain 3 Iteration: 2700 / 3000 [ 90%] (Sampling)
Chain 3 Iteration: 2800 / 3000 [ 93%] (Sampling)
Chain 4 Iteration: 3000 / 3000 [100%] (Sampling)
Chain 4 finished in 1.4 seconds.
Chain 1 Iteration: 2900 / 3000 [ 96%] (Sampling)
Chain 2 Iteration: 2800 / 3000 [ 93%] (Sampling)
Chain 2 Iteration: 2900 / 3000 [ 96%] (Sampling)
Chain 2 Iteration: 3000 / 3000 [100%] (Sampling)
Chain 3 Iteration: 2900 / 3000 [ 96%] (Sampling)
Chain 3 Iteration: 3000 / 3000 [100%] (Sampling)
Chain 2 finished in 1.6 seconds.
Chain 3 finished in 1.6 seconds.
Chain 1 Iteration: 3000 / 3000 [100%] (Sampling)
Chain 1 finished in 1.6 seconds.
All 4 chains finished successfully.
Mean chain execution time: 1.6 seconds.
Total execution time: 1.8 seconds.fit_n$summary()# A tibble: 4 × 10
variable mean median sd mad q5 q95 rhat ess_bulk
<chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 lp__ -461. -460. 1.24 1.02 -463. -459. 1.00 3681.
2 alpha 2.19 2.19 0.0816 0.0820 2.06 2.33 1.00 4263.
3 beta -0.307 -0.307 0.0319 0.0316 -0.360 -0.254 1.00 4313.
4 k 1.76 1.76 0.0948 0.0935 1.61 1.92 1.00 5299.
# ℹ 1 more variable: ess_tail <dbl>In this parametrization, the outcome variable \(t_i\)Note that this measurement process will generate an integer valued response. However, we know that if the value of \(t_i = t\), then in reality \(t_i \in (t - 1, t]\), and we can never know the true value of \(t_i\) because we don’t do inspections more often.
dat_censored <- list()
dat_censored$N <- nrow(sim_data)
dat_censored$x <- sim_data$x
dat_censored$y1 <- sim_data$t - 1
dat_censored$y2 <- sim_data$t
str(dat_censored)List of 4
$ N : int 210
$ x : int [1:210] 4 3 4 1 1 4 3 1 1 1 ...
$ y1: num [1:210] 0 3 2 10 9 0 2 3 1 3 ...
$ y2: num [1:210] 1 4 3 11 10 1 3 4 2 4 ...mod_pth <- here::here(pth_base, "Ex5b.stan")
mod_c <- cmdstanr::cmdstan_model(mod_pth, compile = FALSE)
mod_c$compile(pedantic = TRUE, force_recompile = TRUE)In file included from stan/lib/stan_math/stan/math/prim/prob/von_mises_lccdf.hpp:5,
from stan/lib/stan_math/stan/math/prim/prob/von_mises_ccdf_log.hpp:4,
from stan/lib/stan_math/stan/math/prim/prob.hpp:356,
from stan/lib/stan_math/stan/math/prim.hpp:16,
from stan/lib/stan_math/stan/math/rev.hpp:14,
from stan/lib/stan_math/stan/math.hpp:19,
from stan/src/stan/model/model_header.hpp:4,
from C:/Users/Zane/AppData/Local/Temp/RtmpkPQFPJ/model-4f187f6c53aa.hpp:2:
stan/lib/stan_math/stan/math/prim/prob/von_mises_cdf.hpp: In function 'stan::return_type_t<T_x, T_sigma, T_l> stan::math::von_mises_cdf(const T_x&, const T_mu&, const T_k&)':
stan/lib/stan_math/stan/math/prim/prob/von_mises_cdf.hpp:194: note: '-Wmisleading-indentation' is disabled from this point onwards, since column-tracking was disabled due to the size of the code/headers
194 | if (cdf_n < 0.0)
| stan/lib/stan_math/stan/math/prim/prob/von_mises_cdf.hpp:194: note: adding '-flarge-source-files' will allow for more column-tracking support, at the expense of compilation time and memoryfit_c <- mod_c$sample(
dat_censored,
seed = 3248315,
parallel_chains = 4,
iter_warmup = 500,
iter_sampling = 2500,
show_messages = T
)Running MCMC with 4 parallel chains...Chain 1 Rejecting initial value:Chain 1 Log probability evaluates to log(0), i.e. negative infinity.Chain 1 Stan can't start sampling from this initial value.Chain 1 Iteration: 1 / 3000 [ 0%] (Warmup)
Chain 2 Iteration: 1 / 3000 [ 0%] (Warmup)
Chain 3 Iteration: 1 / 3000 [ 0%] (Warmup)
Chain 4 Iteration: 1 / 3000 [ 0%] (Warmup)
Chain 1 Iteration: 100 / 3000 [ 3%] (Warmup)
Chain 1 Iteration: 200 / 3000 [ 6%] (Warmup)
Chain 2 Iteration: 100 / 3000 [ 3%] (Warmup)
Chain 2 Iteration: 200 / 3000 [ 6%] (Warmup)
Chain 3 Iteration: 100 / 3000 [ 3%] (Warmup)
Chain 3 Iteration: 200 / 3000 [ 6%] (Warmup)
Chain 4 Iteration: 100 / 3000 [ 3%] (Warmup)
Chain 4 Iteration: 200 / 3000 [ 6%] (Warmup)
Chain 1 Iteration: 300 / 3000 [ 10%] (Warmup)
Chain 2 Iteration: 300 / 3000 [ 10%] (Warmup)
Chain 3 Iteration: 300 / 3000 [ 10%] (Warmup)
Chain 4 Iteration: 300 / 3000 [ 10%] (Warmup)
Chain 1 Iteration: 400 / 3000 [ 13%] (Warmup)
Chain 2 Iteration: 400 / 3000 [ 13%] (Warmup)
Chain 3 Iteration: 400 / 3000 [ 13%] (Warmup)
Chain 4 Iteration: 400 / 3000 [ 13%] (Warmup)
Chain 1 Iteration: 500 / 3000 [ 16%] (Warmup)
Chain 1 Iteration: 501 / 3000 [ 16%] (Sampling)
Chain 2 Iteration: 500 / 3000 [ 16%] (Warmup)
Chain 2 Iteration: 501 / 3000 [ 16%] (Sampling)
Chain 3 Iteration: 500 / 3000 [ 16%] (Warmup)
Chain 3 Iteration: 501 / 3000 [ 16%] (Sampling)
Chain 4 Iteration: 500 / 3000 [ 16%] (Warmup)
Chain 4 Iteration: 501 / 3000 [ 16%] (Sampling)
Chain 1 Iteration: 600 / 3000 [ 20%] (Sampling)
Chain 2 Iteration: 600 / 3000 [ 20%] (Sampling)
Chain 3 Iteration: 600 / 3000 [ 20%] (Sampling)
Chain 4 Iteration: 600 / 3000 [ 20%] (Sampling)
Chain 1 Iteration: 700 / 3000 [ 23%] (Sampling)
Chain 2 Iteration: 700 / 3000 [ 23%] (Sampling)
Chain 3 Iteration: 700 / 3000 [ 23%] (Sampling)
Chain 4 Iteration: 700 / 3000 [ 23%] (Sampling)
Chain 2 Iteration: 800 / 3000 [ 26%] (Sampling)
Chain 3 Iteration: 800 / 3000 [ 26%] (Sampling)
Chain 4 Iteration: 800 / 3000 [ 26%] (Sampling)
Chain 1 Iteration: 800 / 3000 [ 26%] (Sampling)
Chain 2 Iteration: 900 / 3000 [ 30%] (Sampling)
Chain 3 Iteration: 900 / 3000 [ 30%] (Sampling)
Chain 4 Iteration: 900 / 3000 [ 30%] (Sampling)
Chain 1 Iteration: 900 / 3000 [ 30%] (Sampling)
Chain 3 Iteration: 1000 / 3000 [ 33%] (Sampling)
Chain 3 Iteration: 1100 / 3000 [ 36%] (Sampling)
Chain 4 Iteration: 1000 / 3000 [ 33%] (Sampling)
Chain 1 Iteration: 1000 / 3000 [ 33%] (Sampling)
Chain 2 Iteration: 1000 / 3000 [ 33%] (Sampling)
Chain 3 Iteration: 1200 / 3000 [ 40%] (Sampling)
Chain 4 Iteration: 1100 / 3000 [ 36%] (Sampling)
Chain 1 Iteration: 1100 / 3000 [ 36%] (Sampling)
Chain 2 Iteration: 1100 / 3000 [ 36%] (Sampling)
Chain 3 Iteration: 1300 / 3000 [ 43%] (Sampling)
Chain 4 Iteration: 1200 / 3000 [ 40%] (Sampling)
Chain 1 Iteration: 1200 / 3000 [ 40%] (Sampling)
Chain 2 Iteration: 1200 / 3000 [ 40%] (Sampling)
Chain 3 Iteration: 1400 / 3000 [ 46%] (Sampling)
Chain 4 Iteration: 1300 / 3000 [ 43%] (Sampling)
Chain 1 Iteration: 1300 / 3000 [ 43%] (Sampling)
Chain 2 Iteration: 1300 / 3000 [ 43%] (Sampling)
Chain 3 Iteration: 1500 / 3000 [ 50%] (Sampling)
Chain 4 Iteration: 1400 / 3000 [ 46%] (Sampling)
Chain 1 Iteration: 1400 / 3000 [ 46%] (Sampling)
Chain 2 Iteration: 1400 / 3000 [ 46%] (Sampling)
Chain 3 Iteration: 1600 / 3000 [ 53%] (Sampling)
Chain 3 Iteration: 1700 / 3000 [ 56%] (Sampling)
Chain 4 Iteration: 1500 / 3000 [ 50%] (Sampling)
Chain 1 Iteration: 1500 / 3000 [ 50%] (Sampling)
Chain 2 Iteration: 1500 / 3000 [ 50%] (Sampling)
Chain 3 Iteration: 1800 / 3000 [ 60%] (Sampling)
Chain 4 Iteration: 1600 / 3000 [ 53%] (Sampling)
Chain 1 Iteration: 1600 / 3000 [ 53%] (Sampling)
Chain 3 Iteration: 1900 / 3000 [ 63%] (Sampling)
Chain 4 Iteration: 1700 / 3000 [ 56%] (Sampling)
Chain 2 Iteration: 1600 / 3000 [ 53%] (Sampling)
Chain 3 Iteration: 2000 / 3000 [ 66%] (Sampling)
Chain 4 Iteration: 1800 / 3000 [ 60%] (Sampling)
Chain 1 Iteration: 1700 / 3000 [ 56%] (Sampling)
Chain 2 Iteration: 1700 / 3000 [ 56%] (Sampling)
Chain 3 Iteration: 2100 / 3000 [ 70%] (Sampling)
Chain 3 Iteration: 2200 / 3000 [ 73%] (Sampling)
Chain 1 Iteration: 1800 / 3000 [ 60%] (Sampling)
Chain 2 Iteration: 1800 / 3000 [ 60%] (Sampling)
Chain 3 Iteration: 2300 / 3000 [ 76%] (Sampling)
Chain 4 Iteration: 1900 / 3000 [ 63%] (Sampling)
Chain 1 Iteration: 1900 / 3000 [ 63%] (Sampling)
Chain 2 Iteration: 1900 / 3000 [ 63%] (Sampling)
Chain 3 Iteration: 2400 / 3000 [ 80%] (Sampling)
Chain 4 Iteration: 2000 / 3000 [ 66%] (Sampling)
Chain 4 Iteration: 2100 / 3000 [ 70%] (Sampling)
Chain 1 Iteration: 2000 / 3000 [ 66%] (Sampling)
Chain 2 Iteration: 2000 / 3000 [ 66%] (Sampling)
Chain 3 Iteration: 2500 / 3000 [ 83%] (Sampling)
Chain 4 Iteration: 2200 / 3000 [ 73%] (Sampling)
Chain 1 Iteration: 2100 / 3000 [ 70%] (Sampling)
Chain 2 Iteration: 2100 / 3000 [ 70%] (Sampling)
Chain 3 Iteration: 2600 / 3000 [ 86%] (Sampling)
Chain 1 Iteration: 2200 / 3000 [ 73%] (Sampling)
Chain 2 Iteration: 2200 / 3000 [ 73%] (Sampling)
Chain 3 Iteration: 2700 / 3000 [ 90%] (Sampling)
Chain 3 Iteration: 2800 / 3000 [ 93%] (Sampling)
Chain 4 Iteration: 2300 / 3000 [ 76%] (Sampling)
Chain 3 Iteration: 2900 / 3000 [ 96%] (Sampling)
Chain 4 Iteration: 2400 / 3000 [ 80%] (Sampling)
Chain 1 Iteration: 2300 / 3000 [ 76%] (Sampling)
Chain 2 Iteration: 2300 / 3000 [ 76%] (Sampling)
Chain 3 Iteration: 3000 / 3000 [100%] (Sampling)
Chain 4 Iteration: 2500 / 3000 [ 83%] (Sampling)
Chain 3 finished in 3.0 seconds.
Chain 1 Iteration: 2400 / 3000 [ 80%] (Sampling)
Chain 2 Iteration: 2400 / 3000 [ 80%] (Sampling)
Chain 4 Iteration: 2600 / 3000 [ 86%] (Sampling)
Chain 1 Iteration: 2500 / 3000 [ 83%] (Sampling)
Chain 2 Iteration: 2500 / 3000 [ 83%] (Sampling)
Chain 4 Iteration: 2700 / 3000 [ 90%] (Sampling)
Chain 1 Iteration: 2600 / 3000 [ 86%] (Sampling)
Chain 2 Iteration: 2600 / 3000 [ 86%] (Sampling)
Chain 4 Iteration: 2800 / 3000 [ 93%] (Sampling)
Chain 1 Iteration: 2700 / 3000 [ 90%] (Sampling)
Chain 2 Iteration: 2700 / 3000 [ 90%] (Sampling)
Chain 4 Iteration: 2900 / 3000 [ 96%] (Sampling)
Chain 1 Iteration: 2800 / 3000 [ 93%] (Sampling)
Chain 2 Iteration: 2800 / 3000 [ 93%] (Sampling)
Chain 4 Iteration: 3000 / 3000 [100%] (Sampling)
Chain 4 finished in 3.5 seconds.
Chain 1 Iteration: 2900 / 3000 [ 96%] (Sampling)
Chain 2 Iteration: 2900 / 3000 [ 96%] (Sampling)
Chain 1 Iteration: 3000 / 3000 [100%] (Sampling)
Chain 1 finished in 3.8 seconds.
Chain 2 Iteration: 3000 / 3000 [100%] (Sampling)
Chain 2 finished in 3.8 seconds.
All 4 chains finished successfully.
Mean chain execution time: 3.5 seconds.
Total execution time: 4.0 seconds.fit_c$summary()# A tibble: 4 × 10
variable mean median sd mad q5 q95 rhat ess_bulk
<chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 lp__ -458. -457. 1.26 1.02 -460. -456. 1.00 4046.
2 alpha 2.12 2.12 0.101 0.0977 1.96 2.29 1.00 3599.
3 beta -0.355 -0.354 0.0401 0.0399 -0.421 -0.288 1.00 3669.
4 k 1.44 1.44 0.0874 0.0859 1.30 1.59 1.00 5322.
# ℹ 1 more variable: ess_tail <dbl>We can introduce more