6  Example Model 4: Logistic regression with censored predictors

For the next example model we have enough background knowledge to implement a model for a problem that my group has been trying to tackle recently, and that is somewhat common with the type of data that I work with. Suppose we want to test the efficacy of a novel vaccine candidate in a clinical trial.

Typically, these vaccines have immunological correlates of protection, some value we can measure that gives a general idea of how strong a person’s immune response was, and correlates with their probability of getting a disease. One of the most common types of these measurements are antibody titers, where typically a high antibody titer is protective and corresponds to a lower probability of disease. If we have a clinical trial where we record if patients get the disease (after challenge or after a sufficiently long followup period, for this example the details are not too important as long as we assume the infection status is measured accurately), we can model how these measurements are related to protection via logistic regression.

6.1 Model with one patient group

For the first model, we’ll consider a simpler case where we only have one group of patients. This model would be appropriate for, e.g., an observational study where all patients are given the vaccine of interest.

The data generating model is as follows:

\[ \begin{align*} y_i &\sim \text{Bernoulli}\left(p\right) \\ \mathrm{logit}(p) &= \alpha + \beta \cdot x_i \end{align*} \] where \(y_i\) is a binary outcome where 1 indicates infection and 0 indicates no infection, and \(x_i\) is our antibody titer. However, the specific problem we deal with in practice is that these antibody titers tend to have lower limits of detection. Thus, we need to add an observation model to our data generating process to reflect the incomplete observations we obtain of \(x\).

\[ \begin{align*} y_i &\sim \text{Bernoulli}\left(p_i\right) \\ \mathrm{logit}(p_i) &= \alpha + \beta \cdot x^*_i \\ x_i^* &\sim \mathrm{Normal}\left(\mu_x, \sigma^2_x\right) \\ x_i &= \begin{cases} \frac{1}{2}\mathrm{LoD}, & x^*_i < \mathrm{LoD} \\ x^*_i, & x^*_i \geq \mathrm{LoD} \end{cases} \\ \end{align*} \] Here, we assume that we work with the \(x\) variable on the log scale at all times,
mostly cause it’s annoying and confusing to write out all the logs every time, so we could also write \[x_i^* = \mathrm{log} \left(z^*_i\right)\] and say \(z^*_i\) is the actual latent un-logged titer.

Now that we have the data generating process written out, we can simulate some example data. Note that in this example, we can interpret \(\alpha\) as the log-odds of infection if a person were to have no antibodies. For example, if we assume that this probability is \(50\%\) we would apply the logit transformation to get that \(\alpha = 0\). However, let’s assume that the inoculum dose is quite high and during our subject selection process we’ve included anyone who might have a genetic resistance to the disease (i.e., FUT2- individuals for norovirus). So let’s say if a person has zero antibodies, their probably of getting sick should be \(90\%\). Then, \(\log(0.9 / 0.1) \approx 2.2\).

We then want our true \(\beta\) value to be negative, indicating that as the number of antibodies rise, the log-odds of infection decrease. We can interpret \(\beta\) as the change in the log-odds ratio associated with a one-unit change in antibody titer – the nonlinearity here makes it a bit more difficult to interpret this effect. We can, however, intercept \(\exp(\beta)\) as the odds ratio between individuals with titer \(x_i + 1\) and individuals with titer \(x_i\). This corresponds to a nonlinear change in risk that depends on the value of \(x_i\). However, if we want the odds of infection to halve for each 1 unit increase in antibody titer, we would set \(\beta = -\log(2) \approx -0.7\).

set.seed(134125)
sim_parms <- list(
    n = 110,
    alpha = 2.2,
    beta = -1.37,
    mu_x = 2,
    sigma_x = 2,
    LoD = 0
)

inv_logit <- function(x) {return(1 / (1 + exp(-x)))}

sim_one_group <- function(n, alpha, beta, mu_x, sigma_x, LoD) {
    out <- tibble::tibble(
        x_star = rnorm(n, mu_x, sigma_x),
        x = ifelse(x_star < LoD, 0.5 * LoD, x_star),
        p = inv_logit(alpha + beta * x_star),
        y = rbinom(n, size = 1, prob = p)
    )
}

sim_data <- do.call(sim_one_group, sim_parms)

Of course visualizing the relationship between a binary outcome and a continuous predictor is in some sense more complex than visualizing the relationship between a continuous outcome and a continuous predictor.

First, let’s look at how the distribution of the predictor variable changes if we condition on the outcome.

sim_data |>
    tidyr::pivot_longer(cols = c(x, x_star)) |>
    dplyr::mutate(
        yf = factor(
            y,
            levels = c(0, 1),
            labels = c("Not infected", "Infected")
        ),
        name = factor(
            name,
            levels = c("x_star", "x"),
            labels = c("Latent variable", "Observed variable")
        )
    ) |>
    ggplot() +
    aes(x = value, fill = yf) +
    geom_vline(
        xintercept = 0,
        linetype = "dashed",
        color = "black",
        linewidth = 1
    ) +
    geom_histogram(
        binwidth = 0.5, boundary = 0, closed = "left",
        position = "identity", alpha = 0.6,
        color = "black"
    ) +
    scale_x_continuous(
        name = "Simulated log titer",
        breaks = scales::breaks_pretty()
    ) +
    scale_y_continuous(breaks = scales::breaks_pretty()) +
    scale_fill_brewer(palette = "Dark2", name = NULL) +
    facet_wrap(facets = vars(name))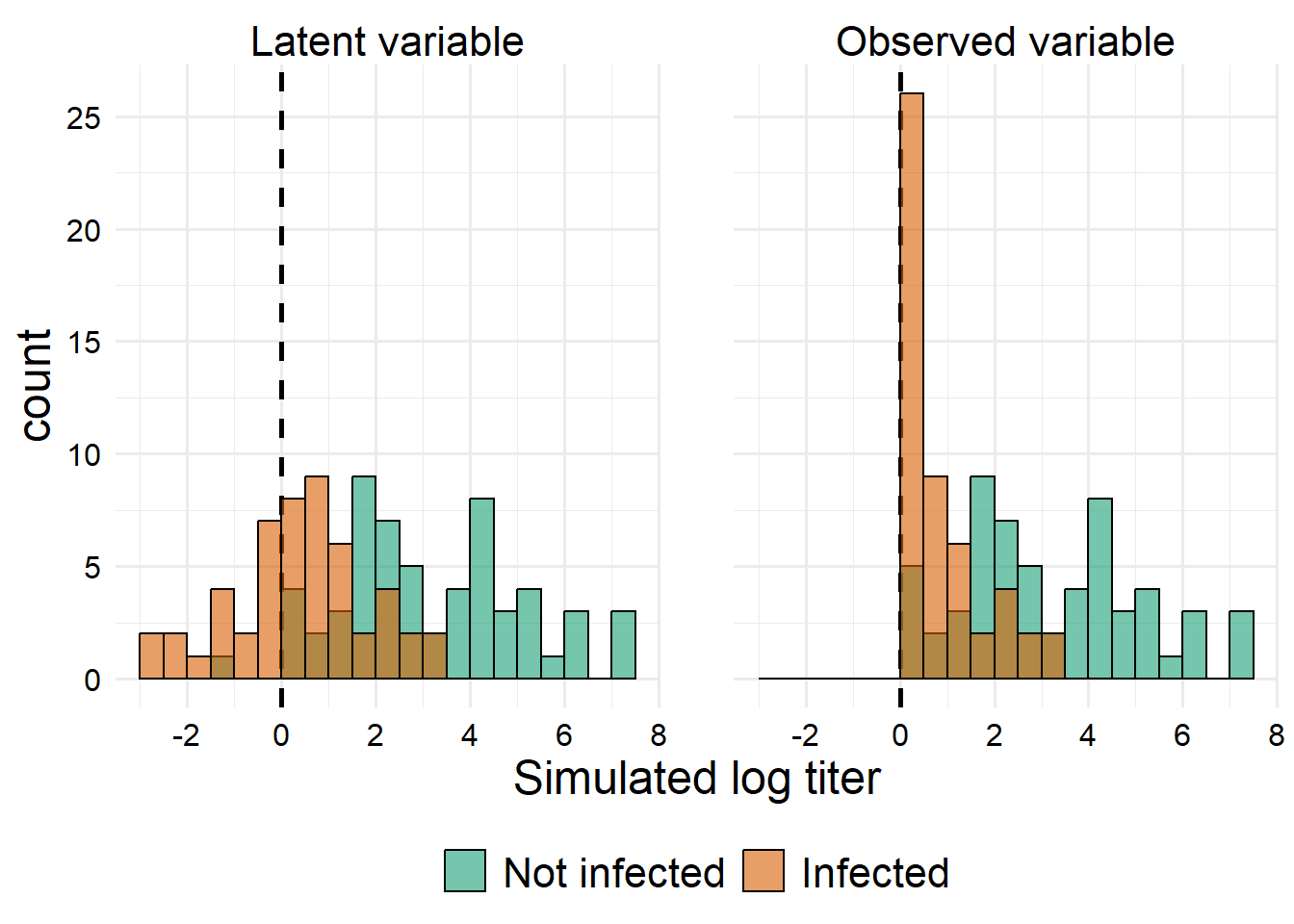

Essentially everything below our lower threshold gets bumped up, which will make the summary statistics of the distribution more similar between groups for the observed titer values than they would have been for the latent titer values. However, we can still see a large difference.

interp <-
    tibble::tibble(
        value = seq(-2, 6, 0.1),
        p = inv_logit(sim_parms$alpha + sim_parms$beta * value)
    )

interp2 <-
    dplyr::bind_rows(
        "Latent variable" = interp,
        "Observed variable" = interp,
        .id = "name"
    )

lab1 <- latex2exp::TeX(r"($Pr(y_{i} = 1 \ | \ x_{i})$)")

sim_data |>
    tidyr::pivot_longer(cols = c(x, x_star)) |>
    dplyr::mutate(
        yf = factor(
            y,
            levels = c(0, 1),
            labels = c("Not infected", "Infected")
        ),
        name = factor(
            name,
            levels = c("x_star", "x"),
            labels = c("Latent variable", "Observed variable")
        )
    ) |>
    ggplot() +
    aes(x = value, color = name) +
    geom_line(
        data = interp2, aes(y = p), color = "darkgray", linetype = 2, linewidth = 1
    ) +
    geom_point(
        aes(y = y), size = 3, alpha = 0.5,
        position = position_jitter(width = 0, height = 0.05, seed = 370)
    ) +
    scale_x_continuous(
        name = "Simulated log titer",
        breaks = scales::breaks_pretty()
    ) +
    scale_y_continuous(
        name = lab1,
        breaks = scales::breaks_pretty()
    ) +
    scale_color_brewer(palette = "Accent", name = NULL) +
    facet_wrap(facets = vars(name))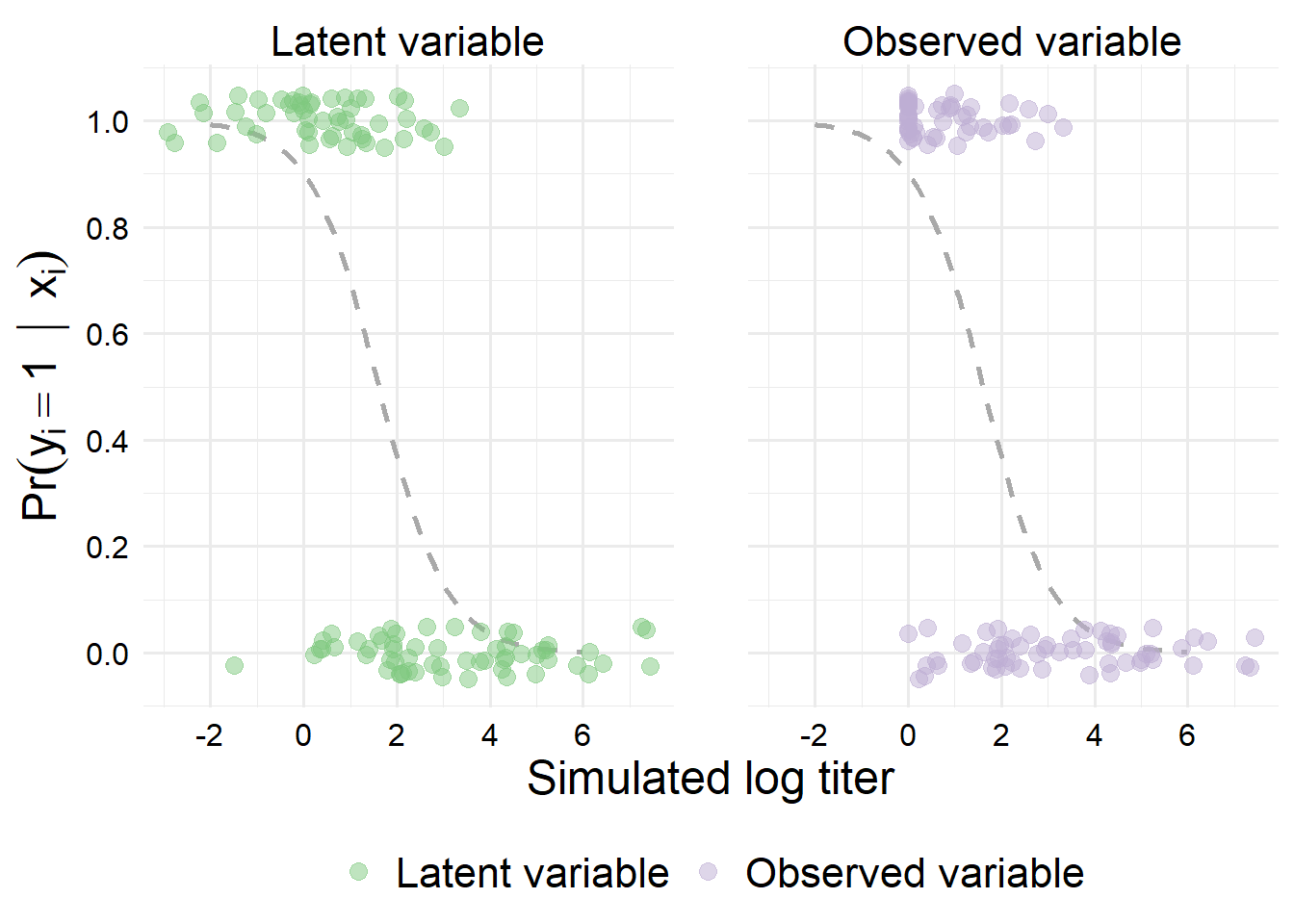

data_list <-
    sim_data |>
    dplyr::mutate(x_l = sim_parms$LoD) |>
    dplyr::select(x, x_l, y) |>
    as.list()

data_list$N <- sim_parms$n

str(data_list)

List of 4
 $ x  : num [1:110] 0.123 1.872 0.932 1.865 1.925 ...
 $ x_l: num [1:110] 0 0 0 0 0 0 0 0 0 0 ...
 $ y  : int [1:110] 1 0 1 0 0 0 1 0 0 0 ...
 $ N  : num 110

mod_pth <- here::here(pth_base, "Ex4a.stan")
mod <- cmdstanr::cmdstan_model(mod_pth, compile = FALSE)
mod$compile(force_recompile = TRUE, pedantic = TRUE)

In file included from stan/lib/stan_math/stan/math/prim/prob/von_mises_lccdf.hpp:5,
                 from stan/lib/stan_math/stan/math/prim/prob/von_mises_ccdf_log.hpp:4,
                 from stan/lib/stan_math/stan/math/prim/prob.hpp:356,
                 from stan/lib/stan_math/stan/math/prim.hpp:16,
                 from stan/lib/stan_math/stan/math/rev.hpp:14,
                 from stan/lib/stan_math/stan/math.hpp:19,
                 from stan/src/stan/model/model_header.hpp:4,
                 from C:/Users/Zane/AppData/Local/Temp/Rtmp0aU2FX/model-374c30036286.hpp:2:
stan/lib/stan_math/stan/math/prim/prob/von_mises_cdf.hpp: In function 'stan::return_type_t<T_x, T_sigma, T_l> stan::math::von_mises_cdf(const T_x&, const T_mu&, const T_k&)':
stan/lib/stan_math/stan/math/prim/prob/von_mises_cdf.hpp:194: note: '-Wmisleading-indentation' is disabled from this point onwards, since column-tracking was disabled due to the size of the code/headers
  194 |       if (cdf_n < 0.0)
      | 

stan/lib/stan_math/stan/math/prim/prob/von_mises_cdf.hpp:194: note: adding '-flarge-source-files' will allow for more column-tracking support, at the expense of compilation time and memory

fit <- mod$sample(
    data_list,
    seed = 25452345,
    parallel_chains = 4,
    iter_warmup = 500,
    iter_sampling = 2500,
    show_messages = T
)

Running MCMC with 4 parallel chains...

Chain 1 Iteration:    1 / 3000 [  0%]  (Warmup) 
Chain 1 Iteration:  100 / 3000 [  3%]  (Warmup) 
Chain 1 Iteration:  200 / 3000 [  6%]  (Warmup) 
Chain 1 Iteration:  300 / 3000 [ 10%]  (Warmup) 
Chain 1 Iteration:  400 / 3000 [ 13%]  (Warmup) 
Chain 1 Iteration:  500 / 3000 [ 16%]  (Warmup) 
Chain 1 Iteration:  501 / 3000 [ 16%]  (Sampling) 
Chain 1 Iteration:  600 / 3000 [ 20%]  (Sampling) 
Chain 1 Iteration:  700 / 3000 [ 23%]  (Sampling) 
Chain 1 Iteration:  800 / 3000 [ 26%]  (Sampling) 
Chain 1 Iteration:  900 / 3000 [ 30%]  (Sampling) 
Chain 1 Iteration: 1000 / 3000 [ 33%]  (Sampling) 
Chain 2 Iteration:    1 / 3000 [  0%]  (Warmup) 
Chain 2 Iteration:  100 / 3000 [  3%]  (Warmup) 
Chain 2 Iteration:  200 / 3000 [  6%]  (Warmup) 
Chain 2 Iteration:  300 / 3000 [ 10%]  (Warmup) 
Chain 2 Iteration:  400 / 3000 [ 13%]  (Warmup) 
Chain 2 Iteration:  500 / 3000 [ 16%]  (Warmup) 
Chain 2 Iteration:  501 / 3000 [ 16%]  (Sampling) 
Chain 2 Iteration:  600 / 3000 [ 20%]  (Sampling) 
Chain 2 Iteration:  700 / 3000 [ 23%]  (Sampling) 
Chain 2 Iteration:  800 / 3000 [ 26%]  (Sampling) 
Chain 2 Iteration:  900 / 3000 [ 30%]  (Sampling) 
Chain 3 Iteration:    1 / 3000 [  0%]  (Warmup) 
Chain 3 Iteration:  100 / 3000 [  3%]  (Warmup) 
Chain 3 Iteration:  200 / 3000 [  6%]  (Warmup) 
Chain 3 Iteration:  300 / 3000 [ 10%]  (Warmup) 
Chain 3 Iteration:  400 / 3000 [ 13%]  (Warmup) 
Chain 3 Iteration:  500 / 3000 [ 16%]  (Warmup) 
Chain 3 Iteration:  501 / 3000 [ 16%]  (Sampling) 
Chain 3 Iteration:  600 / 3000 [ 20%]  (Sampling) 
Chain 3 Iteration:  700 / 3000 [ 23%]  (Sampling) 
Chain 3 Iteration:  800 / 3000 [ 26%]  (Sampling) 
Chain 4 Iteration:    1 / 3000 [  0%]  (Warmup) 
Chain 4 Iteration:  100 / 3000 [  3%]  (Warmup) 
Chain 4 Iteration:  200 / 3000 [  6%]  (Warmup) 
Chain 4 Iteration:  300 / 3000 [ 10%]  (Warmup) 
Chain 4 Iteration:  400 / 3000 [ 13%]  (Warmup) 
Chain 4 Iteration:  500 / 3000 [ 16%]  (Warmup) 
Chain 4 Iteration:  501 / 3000 [ 16%]  (Sampling) 
Chain 4 Iteration:  600 / 3000 [ 20%]  (Sampling) 

Chain 4 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:

Chain 4 Exception: normal_lpdf: Scale parameter is 0, but must be positive! (in 'C:/Users/Zane/AppData/Local/Temp/Rtmp0aU2FX/model-374c30036286.stan', line 59, column 3 to column 32)

Chain 4 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,

Chain 4 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.

Chain 4 

Chain 1 Iteration: 1100 / 3000 [ 36%]  (Sampling) 
Chain 1 Iteration: 1200 / 3000 [ 40%]  (Sampling) 
Chain 1 Iteration: 1300 / 3000 [ 43%]  (Sampling) 
Chain 1 Iteration: 1400 / 3000 [ 46%]  (Sampling) 
Chain 1 Iteration: 1500 / 3000 [ 50%]  (Sampling) 
Chain 1 Iteration: 1600 / 3000 [ 53%]  (Sampling) 
Chain 1 Iteration: 1700 / 3000 [ 56%]  (Sampling) 
Chain 1 Iteration: 1800 / 3000 [ 60%]  (Sampling) 
Chain 1 Iteration: 1900 / 3000 [ 63%]  (Sampling) 
Chain 1 Iteration: 2000 / 3000 [ 66%]  (Sampling) 
Chain 1 Iteration: 2100 / 3000 [ 70%]  (Sampling) 
Chain 1 Iteration: 2200 / 3000 [ 73%]  (Sampling) 
Chain 1 Iteration: 2300 / 3000 [ 76%]  (Sampling) 
Chain 1 Iteration: 2400 / 3000 [ 80%]  (Sampling) 
Chain 1 Iteration: 2500 / 3000 [ 83%]  (Sampling) 
Chain 1 Iteration: 2600 / 3000 [ 86%]  (Sampling) 
Chain 1 Iteration: 2700 / 3000 [ 90%]  (Sampling) 
Chain 1 Iteration: 2800 / 3000 [ 93%]  (Sampling) 
Chain 1 Iteration: 2900 / 3000 [ 96%]  (Sampling) 
Chain 1 Iteration: 3000 / 3000 [100%]  (Sampling) 
Chain 1 finished in 0.4 seconds.
Chain 2 Iteration: 1000 / 3000 [ 33%]  (Sampling) 
Chain 2 Iteration: 1100 / 3000 [ 36%]  (Sampling) 
Chain 2 Iteration: 1200 / 3000 [ 40%]  (Sampling) 
Chain 2 Iteration: 1300 / 3000 [ 43%]  (Sampling) 
Chain 2 Iteration: 1400 / 3000 [ 46%]  (Sampling) 
Chain 2 Iteration: 1500 / 3000 [ 50%]  (Sampling) 
Chain 2 Iteration: 1600 / 3000 [ 53%]  (Sampling) 
Chain 2 Iteration: 1700 / 3000 [ 56%]  (Sampling) 
Chain 2 Iteration: 1800 / 3000 [ 60%]  (Sampling) 
Chain 2 Iteration: 1900 / 3000 [ 63%]  (Sampling) 
Chain 2 Iteration: 2000 / 3000 [ 66%]  (Sampling) 
Chain 2 Iteration: 2100 / 3000 [ 70%]  (Sampling) 
Chain 2 Iteration: 2200 / 3000 [ 73%]  (Sampling) 
Chain 2 Iteration: 2300 / 3000 [ 76%]  (Sampling) 
Chain 2 Iteration: 2400 / 3000 [ 80%]  (Sampling) 
Chain 2 Iteration: 2500 / 3000 [ 83%]  (Sampling) 
Chain 2 Iteration: 2600 / 3000 [ 86%]  (Sampling) 
Chain 2 Iteration: 2700 / 3000 [ 90%]  (Sampling) 
Chain 2 Iteration: 2800 / 3000 [ 93%]  (Sampling) 
Chain 2 Iteration: 2900 / 3000 [ 96%]  (Sampling) 
Chain 2 Iteration: 3000 / 3000 [100%]  (Sampling) 
Chain 2 finished in 0.3 seconds.
Chain 3 Iteration:  900 / 3000 [ 30%]  (Sampling) 
Chain 3 Iteration: 1000 / 3000 [ 33%]  (Sampling) 
Chain 3 Iteration: 1100 / 3000 [ 36%]  (Sampling) 
Chain 3 Iteration: 1200 / 3000 [ 40%]  (Sampling) 
Chain 3 Iteration: 1300 / 3000 [ 43%]  (Sampling) 
Chain 3 Iteration: 1400 / 3000 [ 46%]  (Sampling) 
Chain 3 Iteration: 1500 / 3000 [ 50%]  (Sampling) 
Chain 3 Iteration: 1600 / 3000 [ 53%]  (Sampling) 
Chain 3 Iteration: 1700 / 3000 [ 56%]  (Sampling) 
Chain 3 Iteration: 1800 / 3000 [ 60%]  (Sampling) 
Chain 3 Iteration: 1900 / 3000 [ 63%]  (Sampling) 
Chain 3 Iteration: 2000 / 3000 [ 66%]  (Sampling) 
Chain 3 Iteration: 2100 / 3000 [ 70%]  (Sampling) 
Chain 3 Iteration: 2200 / 3000 [ 73%]  (Sampling) 
Chain 3 Iteration: 2300 / 3000 [ 76%]  (Sampling) 
Chain 3 Iteration: 2400 / 3000 [ 80%]  (Sampling) 
Chain 3 Iteration: 2500 / 3000 [ 83%]  (Sampling) 
Chain 3 Iteration: 2600 / 3000 [ 86%]  (Sampling) 
Chain 3 Iteration: 2700 / 3000 [ 90%]  (Sampling) 
Chain 3 Iteration: 2800 / 3000 [ 93%]  (Sampling) 
Chain 3 Iteration: 2900 / 3000 [ 96%]  (Sampling) 
Chain 3 Iteration: 3000 / 3000 [100%]  (Sampling) 
Chain 3 finished in 0.4 seconds.
Chain 4 Iteration:  700 / 3000 [ 23%]  (Sampling) 
Chain 4 Iteration:  800 / 3000 [ 26%]  (Sampling) 
Chain 4 Iteration:  900 / 3000 [ 30%]  (Sampling) 
Chain 4 Iteration: 1000 / 3000 [ 33%]  (Sampling) 
Chain 4 Iteration: 1100 / 3000 [ 36%]  (Sampling) 
Chain 4 Iteration: 1200 / 3000 [ 40%]  (Sampling) 
Chain 4 Iteration: 1300 / 3000 [ 43%]  (Sampling) 
Chain 4 Iteration: 1400 / 3000 [ 46%]  (Sampling) 
Chain 4 Iteration: 1500 / 3000 [ 50%]  (Sampling) 
Chain 4 Iteration: 1600 / 3000 [ 53%]  (Sampling) 
Chain 4 Iteration: 1700 / 3000 [ 56%]  (Sampling) 
Chain 4 Iteration: 1800 / 3000 [ 60%]  (Sampling) 
Chain 4 Iteration: 1900 / 3000 [ 63%]  (Sampling) 
Chain 4 Iteration: 2000 / 3000 [ 66%]  (Sampling) 
Chain 4 Iteration: 2100 / 3000 [ 70%]  (Sampling) 
Chain 4 Iteration: 2200 / 3000 [ 73%]  (Sampling) 
Chain 4 Iteration: 2300 / 3000 [ 76%]  (Sampling) 
Chain 4 Iteration: 2400 / 3000 [ 80%]  (Sampling) 
Chain 4 Iteration: 2500 / 3000 [ 83%]  (Sampling) 
Chain 4 Iteration: 2600 / 3000 [ 86%]  (Sampling) 
Chain 4 Iteration: 2700 / 3000 [ 90%]  (Sampling) 
Chain 4 Iteration: 2800 / 3000 [ 93%]  (Sampling) 
Chain 4 Iteration: 2900 / 3000 [ 96%]  (Sampling) 
Chain 4 Iteration: 3000 / 3000 [100%]  (Sampling) 
Chain 4 finished in 0.4 seconds.

All 4 chains finished successfully.
Mean chain execution time: 0.4 seconds.
Total execution time: 0.6 seconds.

fit$cmdstan_diagnose()

Processing csv files: C:/Users/Zane/AppData/Local/Temp/Rtmp0aU2FX/Ex4a-202403032225-1-7db877.csv, C:/Users/Zane/AppData/Local/Temp/Rtmp0aU2FX/Ex4a-202403032225-2-7db877.csv, C:/Users/Zane/AppData/Local/Temp/Rtmp0aU2FX/Ex4a-202403032225-3-7db877.csv, C:/Users/Zane/AppData/Local/Temp/Rtmp0aU2FX/Ex4a-202403032225-4-7db877.csv

Checking sampler transitions treedepth.
Treedepth satisfactory for all transitions.

Checking sampler transitions for divergences.
No divergent transitions found.

Checking E-BFMI - sampler transitions HMC potential energy.
E-BFMI satisfactory.

Effective sample size satisfactory.

Split R-hat values satisfactory all parameters.

Processing complete, no problems detected.

fit$summary()

# A tibble: 5 × 10
  variable    mean  median    sd   mad      q5      q95  rhat ess_bulk ess_tail
  <chr>      <dbl>   <dbl> <dbl> <dbl>   <dbl>    <dbl> <dbl>    <dbl>    <dbl>
1 lp__     -190.   -189.   1.44  1.21  -192.   -188.     1.00    4408.    5589.
2 alpha       1.91    1.90 0.411 0.416    1.26    2.60   1.00    5508.    5501.
3 beta       -1.23   -1.22 0.226 0.226   -1.62   -0.881  1.00    5323.    5512.
4 mu_x        1.84    1.85 0.234 0.231    1.45    2.22   1.00    8886.    6064.
5 sigma_x     2.32    2.31 0.177 0.174    2.05    2.63   1.00    9161.    6999.

6.2 Effect of vaccine

Of course, a more interesting question is when we have \(k\) different treatment groups. These groups could be vaccine and placebo, like the example that motivated this project, or they could be multiple different vaccine candidates, doses, etc. So we now need to incorporate the effect of the treatment into the model. However, we know that the treatment will have a direct effect on \(x\), the antibody titers, and we can add a direct effect on \(y\) to represent the combined effect of the vaccine on other facets of the immune system (e.g. cell-mediated responses) which explain variations in infection risk that are not due to antibodies.

In this framework, \(x\) becomes a mediator of the relationship between \(t\), the treatment, and \(y\). For simplicity, we model the effect of \(t\) on \(x\), and the effect of \(t\) and \(x\) jointly on \(y\), both as linear functions of the predictors. Specifically, the data generating model is given as follows.

\[ \begin{align*} y_i &\sim \text{Bernoulli}\left(p_i\right) \\ \mathrm{logit}(p_i) &= \beta_{1, T[i]} + \beta_{2, T[i]} \cdot x^*_i \\ \log\left(x_i^*\right) &\sim \mathrm{Normal}\left(\mu_x, \sigma^2_x\right) \\ \mu_x &= \alpha_{T[i]} \\ x_i &= \begin{cases} \frac{1}{2}\mathrm{LoD}, & x^*_i < \mathrm{LoD} \\ x^*_i, & x^*_i \geq \mathrm{LoD} \end{cases} \\ T[i] &= \begin{cases} 1, & \text{individual } i \text{ is in the placebo group} \\ 2, & \text{individual } i \text{ is in the vaccine group} \end{cases} \end{align*} \]

Given the generative model, we can simulate data which follow our assumptions.

set.seed(341341)
# Some parameters are commented out because I originally had a global
# intercept for mu and for p, but then the intercept parameters are
# nonidentifiable under index coding as written.
sim2_parms <- list(
    n = 116,
    #a0 = 2,
    a1 = c(2.5, 4),
    #b0 = 1.5,
    b1 = c(1.7, 2.2),
    b2 = c(-0.67, -1.37),
    sigma_x = 1.5,
    LoD = 3,
    latent = TRUE
)
sim_two_groups <- function(n, b1, b2, a1, sigma_x, LoD,
                                                     latent = TRUE) {
    out <- tibble::tibble(
        # Randomly assign each individual to 1 (placebo) or 2 (vaccine)
        t = rbinom(n, size = 1, prob = 0.5) + 1,
        mu = a1[t],
        x_star = rnorm(n, mu, sigma_x),
        x = dplyr::if_else(x_star < LoD, 0.5 * LoD, x_star),
        p = inv_logit(b1[t] + b2[t] * x_star),
        y = rbinom(n, 1, prob = p)
    )
    
    # If the arg 'latent' is specified as anything other than FALSE, return the
    # latent variables that we don't observe. Otherwise return only (X, y).
    if (isFALSE(latent)) {
        out <- out |> dplyr::select(t, x, y)
    }
    
    return(out)
}
sim_data_4b <- do.call(sim_two_groups, sim2_parms)

tab_dat <-
    sim_data_4b |>
    dplyr::mutate(
        t = factor(
            t,
            levels = c(2, 1),
            labels = c("Vaccine", "Placebo")
        ),
        y = factor(
            y,
            levels = c(1, 0),
            labels = c("Infected", "Not infected")
        )
    )
tab_dat |>
    gtsummary::tbl_cross(
        row = t, col = y,
        label = list(t ~ "Treatment", y ~ "Outcome")
    )

	Outcome		Total
	Infected	Not infected
Treatment
Vaccine	5	49	54
Placebo	28	34	62
Total	33	83	116

Because the data are from a (hypothetical) clinical trial, the typical epidemiological approach to data analysis, if we do not care about the effect of the mediator \(x\) would be to calculate the risk ratio.

tab <- table(tab_dat$t, tab_dat$y, dnn = c("Treatment", "Outcome"))
epiR_out <- epiR::epi.2by2(
    tab,
    method = "cohort.count"
)
epiR_out

             Outcome +    Outcome -      Total                 Inc risk *
Exposed +            5           49         54       9.26 (3.08 to 20.30)
Exposed -           28           34         62     45.16 (32.48 to 58.32)
Total               33           83        116     28.45 (20.46 to 37.57)

Point estimates and 95% CIs:
-------------------------------------------------------------------
Inc risk ratio                                 0.21 (0.09, 0.49)
Inc odds ratio                                 0.12 (0.04, 0.35)
Attrib risk in the exposed *                   -35.90 (-50.50, -21.30)
Attrib fraction in the exposed (%)            -387.74 (-1074.55, -102.54)
Attrib risk in the population *                -16.71 (-31.57, -1.85)
Attrib fraction in the population (%)         -58.75 (-89.23, -33.18)
-------------------------------------------------------------------
Uncorrected chi2 test that OR = 1: chi2(1) = 18.276 Pr>chi2 = <0.001
Fisher exact test that OR = 1: Pr>chi2 = <0.001
 Wald confidence limits
 CI: confidence interval
 * Outcomes per 100 population units 

# This one takes the variables in the opposite direction so easier to do it
# this way
epiDisplay::csi(
    caseexp = tab[[1]],
    controlex = tab[[3]],
    casenonex = tab[[2]],
    controlnonex = tab[[4]]
)

          Exposure
Outcome    Non-exposed Exposed Total
  Negative 34          49      83   
  Positive 28          5       33   
  Total    62          54      116  
                                    
           Rne         Re      Rt   
  Risk     0.45        0.09    0.28 
                                         Estimate Lower95ci Upper95ci
 Risk difference (Re - Rne)              -0.36    -0.5      -0.2     
 Risk ratio                              0.21     0.1       0.45     
 Protective efficacy =(Rne-Re)/Rne*100   79.5     55.46     90.1     
   or percent of risk reduced                                        
 Number needed to treat (NNT)            2.79     2         4.99     
   or -1/(risk difference)                                           

So if we didn’t care about the effect of \(x\) at all, we would conclude that the vaccine appears to be protective with a RR of \(`r round(epiR_out\)massoc.summary[[1, 2]], 2)$ and a 95% CI of $\left(r round(epiR_out\(massoc.summary[[1, 3]], 2) - round(epiR_out\)massoc.summary[[1, 4]], 2)`)$. Note that this analysis is marginal to the censored \(x_i\) values, and since the data generating process for \(y_i\) relies on the latent \(x^*_i\) values, this analysis should not be biased by the censoring process.

However, in our study we specifically want to know how much of the lower risk is explained by the antibody titer, and how much is not. This analysis is more complicated, and requires us to use a regression model. Fortunately we know the data generating process, so writing the Stan code for an accurate model is not too hard.

mod_pth <- here::here(pth_base, "Ex4b.stan")
mod4b <- cmdstanr::cmdstan_model(mod_pth, compile = F)
mod4b$compile(pedantic = TRUE, force_recompile = TRUE)

In file included from stan/lib/stan_math/stan/math/prim/prob/von_mises_lccdf.hpp:5,
                 from stan/lib/stan_math/stan/math/prim/prob/von_mises_ccdf_log.hpp:4,
                 from stan/lib/stan_math/stan/math/prim/prob.hpp:356,
                 from stan/lib/stan_math/stan/math/prim.hpp:16,
                 from stan/lib/stan_math/stan/math/rev.hpp:14,
                 from stan/lib/stan_math/stan/math.hpp:19,
                 from stan/src/stan/model/model_header.hpp:4,
                 from C:/Users/Zane/AppData/Local/Temp/Rtmp0aU2FX/model-374c53c17b4c.hpp:2:
stan/lib/stan_math/stan/math/prim/prob/von_mises_cdf.hpp: In function 'stan::return_type_t<T_x, T_sigma, T_l> stan::math::von_mises_cdf(const T_x&, const T_mu&, const T_k&)':
stan/lib/stan_math/stan/math/prim/prob/von_mises_cdf.hpp:194: note: '-Wmisleading-indentation' is disabled from this point onwards, since column-tracking was disabled due to the size of the code/headers
  194 |       if (cdf_n < 0.0)
      | 

stan/lib/stan_math/stan/math/prim/prob/von_mises_cdf.hpp:194: note: adding '-flarge-source-files' will allow for more column-tracking support, at the expense of compilation time and memory

mod4b_data <- sim_data_4b |>
    dplyr::mutate(x_l = sim2_parms$LoD, t = as.integer(t)) |>
    dplyr::select(t, y, x, x_l) |>
    as.list()

mod4b_data <- c(
    "N" = nrow(sim_data_4b),
    "k" = as.integer(max(mod4b_data$t)),
    mod4b_data
)
str(mod4b_data)

List of 6
 $ N  : int 116
 $ k  : int 2
 $ t  : int [1:116] 1 1 2 1 1 1 2 2 2 2 ...
 $ y  : int [1:116] 1 0 0 0 0 0 0 0 0 0 ...
 $ x  : num [1:116] 1.5 3.19 1.5 3.79 4.7 ...
 $ x_l: num [1:116] 3 3 3 3 3 3 3 3 3 3 ...

paste0(
    "Naruto checked the data and he says:\n",
    round(mean(mod4b_data$x <= mod4b_data$x_l), 4) * 100,
    "% of x values are below the LoD!\nBelieve it!"
) |> cat()

Naruto checked the data and he says:
46.55% of x values are below the LoD!
Believe it!

fit4b <- mod4b$sample(
    mod4b_data,
    seed = 5234521,
    parallel_chains = 4,
    iter_warmup = 500,
    iter_sampling = 2500,
    show_messages = T
)

Running MCMC with 4 parallel chains...

Chain 1 Iteration:    1 / 3000 [  0%]  (Warmup) 
Chain 1 Iteration:  100 / 3000 [  3%]  (Warmup) 

Chain 1 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:

Chain 1 Exception: normal_lcdf: Scale parameter is 0, but must be positive! (in 'C:/Users/Zane/AppData/Local/Temp/Rtmp0aU2FX/model-374c53c17b4c.stan', line 75, column 3 to column 50)

Chain 1 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,

Chain 1 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.

Chain 1 

Chain 2 Iteration:    1 / 3000 [  0%]  (Warmup) 
Chain 2 Iteration:  100 / 3000 [  3%]  (Warmup) 
Chain 3 Iteration:    1 / 3000 [  0%]  (Warmup) 
Chain 3 Iteration:  100 / 3000 [  3%]  (Warmup) 
Chain 4 Iteration:    1 / 3000 [  0%]  (Warmup) 
Chain 4 Iteration:  100 / 3000 [  3%]  (Warmup) 

Chain 4 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:

Chain 4 Exception: normal_lcdf: Scale parameter is 0, but must be positive! (in 'C:/Users/Zane/AppData/Local/Temp/Rtmp0aU2FX/model-374c53c17b4c.stan', line 75, column 3 to column 50)

Chain 4 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,

Chain 4 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.

Chain 4 

Chain 1 Iteration:  200 / 3000 [  6%]  (Warmup) 
Chain 1 Iteration:  300 / 3000 [ 10%]  (Warmup) 
Chain 1 Iteration:  400 / 3000 [ 13%]  (Warmup) 
Chain 1 Iteration:  500 / 3000 [ 16%]  (Warmup) 
Chain 1 Iteration:  501 / 3000 [ 16%]  (Sampling) 
Chain 2 Iteration:  200 / 3000 [  6%]  (Warmup) 
Chain 2 Iteration:  300 / 3000 [ 10%]  (Warmup) 
Chain 2 Iteration:  400 / 3000 [ 13%]  (Warmup) 
Chain 2 Iteration:  500 / 3000 [ 16%]  (Warmup) 
Chain 2 Iteration:  501 / 3000 [ 16%]  (Sampling) 
Chain 3 Iteration:  200 / 3000 [  6%]  (Warmup) 
Chain 3 Iteration:  300 / 3000 [ 10%]  (Warmup) 
Chain 3 Iteration:  400 / 3000 [ 13%]  (Warmup) 
Chain 3 Iteration:  500 / 3000 [ 16%]  (Warmup) 
Chain 3 Iteration:  501 / 3000 [ 16%]  (Sampling) 
Chain 4 Iteration:  200 / 3000 [  6%]  (Warmup) 
Chain 4 Iteration:  300 / 3000 [ 10%]  (Warmup) 
Chain 4 Iteration:  400 / 3000 [ 13%]  (Warmup) 
Chain 1 Iteration:  600 / 3000 [ 20%]  (Sampling) 
Chain 1 Iteration:  700 / 3000 [ 23%]  (Sampling) 
Chain 2 Iteration:  600 / 3000 [ 20%]  (Sampling) 
Chain 2 Iteration:  700 / 3000 [ 23%]  (Sampling) 
Chain 3 Iteration:  600 / 3000 [ 20%]  (Sampling) 
Chain 3 Iteration:  700 / 3000 [ 23%]  (Sampling) 
Chain 4 Iteration:  500 / 3000 [ 16%]  (Warmup) 
Chain 4 Iteration:  501 / 3000 [ 16%]  (Sampling) 
Chain 4 Iteration:  600 / 3000 [ 20%]  (Sampling) 
Chain 4 Iteration:  700 / 3000 [ 23%]  (Sampling) 
Chain 1 Iteration:  800 / 3000 [ 26%]  (Sampling) 
Chain 1 Iteration:  900 / 3000 [ 30%]  (Sampling) 
Chain 1 Iteration: 1000 / 3000 [ 33%]  (Sampling) 
Chain 2 Iteration:  800 / 3000 [ 26%]  (Sampling) 
Chain 2 Iteration:  900 / 3000 [ 30%]  (Sampling) 
Chain 2 Iteration: 1000 / 3000 [ 33%]  (Sampling) 
Chain 3 Iteration:  800 / 3000 [ 26%]  (Sampling) 
Chain 3 Iteration:  900 / 3000 [ 30%]  (Sampling) 
Chain 3 Iteration: 1000 / 3000 [ 33%]  (Sampling) 
Chain 4 Iteration:  800 / 3000 [ 26%]  (Sampling) 
Chain 4 Iteration:  900 / 3000 [ 30%]  (Sampling) 
Chain 1 Iteration: 1100 / 3000 [ 36%]  (Sampling) 
Chain 1 Iteration: 1200 / 3000 [ 40%]  (Sampling) 
Chain 2 Iteration: 1100 / 3000 [ 36%]  (Sampling) 
Chain 3 Iteration: 1100 / 3000 [ 36%]  (Sampling) 
Chain 3 Iteration: 1200 / 3000 [ 40%]  (Sampling) 
Chain 4 Iteration: 1000 / 3000 [ 33%]  (Sampling) 
Chain 4 Iteration: 1100 / 3000 [ 36%]  (Sampling) 
Chain 1 Iteration: 1300 / 3000 [ 43%]  (Sampling) 
Chain 1 Iteration: 1400 / 3000 [ 46%]  (Sampling) 
Chain 2 Iteration: 1200 / 3000 [ 40%]  (Sampling) 
Chain 2 Iteration: 1300 / 3000 [ 43%]  (Sampling) 
Chain 2 Iteration: 1400 / 3000 [ 46%]  (Sampling) 
Chain 3 Iteration: 1300 / 3000 [ 43%]  (Sampling) 
Chain 3 Iteration: 1400 / 3000 [ 46%]  (Sampling) 
Chain 4 Iteration: 1200 / 3000 [ 40%]  (Sampling) 
Chain 4 Iteration: 1300 / 3000 [ 43%]  (Sampling) 
Chain 1 Iteration: 1500 / 3000 [ 50%]  (Sampling) 
Chain 1 Iteration: 1600 / 3000 [ 53%]  (Sampling) 
Chain 1 Iteration: 1700 / 3000 [ 56%]  (Sampling) 
Chain 2 Iteration: 1500 / 3000 [ 50%]  (Sampling) 
Chain 2 Iteration: 1600 / 3000 [ 53%]  (Sampling) 
Chain 3 Iteration: 1500 / 3000 [ 50%]  (Sampling) 
Chain 3 Iteration: 1600 / 3000 [ 53%]  (Sampling) 
Chain 3 Iteration: 1700 / 3000 [ 56%]  (Sampling) 
Chain 4 Iteration: 1400 / 3000 [ 46%]  (Sampling) 
Chain 4 Iteration: 1500 / 3000 [ 50%]  (Sampling) 
Chain 1 Iteration: 1800 / 3000 [ 60%]  (Sampling) 
Chain 1 Iteration: 1900 / 3000 [ 63%]  (Sampling) 
Chain 2 Iteration: 1700 / 3000 [ 56%]  (Sampling) 
Chain 2 Iteration: 1800 / 3000 [ 60%]  (Sampling) 
Chain 3 Iteration: 1800 / 3000 [ 60%]  (Sampling) 
Chain 3 Iteration: 1900 / 3000 [ 63%]  (Sampling) 
Chain 4 Iteration: 1600 / 3000 [ 53%]  (Sampling) 
Chain 4 Iteration: 1700 / 3000 [ 56%]  (Sampling) 
Chain 1 Iteration: 2000 / 3000 [ 66%]  (Sampling) 
Chain 1 Iteration: 2100 / 3000 [ 70%]  (Sampling) 
Chain 2 Iteration: 1900 / 3000 [ 63%]  (Sampling) 
Chain 3 Iteration: 2000 / 3000 [ 66%]  (Sampling) 
Chain 3 Iteration: 2100 / 3000 [ 70%]  (Sampling) 
Chain 4 Iteration: 1800 / 3000 [ 60%]  (Sampling) 
Chain 4 Iteration: 1900 / 3000 [ 63%]  (Sampling) 
Chain 1 Iteration: 2200 / 3000 [ 73%]  (Sampling) 
Chain 1 Iteration: 2300 / 3000 [ 76%]  (Sampling) 
Chain 2 Iteration: 2000 / 3000 [ 66%]  (Sampling) 
Chain 2 Iteration: 2100 / 3000 [ 70%]  (Sampling) 
Chain 2 Iteration: 2200 / 3000 [ 73%]  (Sampling) 
Chain 3 Iteration: 2200 / 3000 [ 73%]  (Sampling) 
Chain 3 Iteration: 2300 / 3000 [ 76%]  (Sampling) 
Chain 4 Iteration: 2000 / 3000 [ 66%]  (Sampling) 
Chain 4 Iteration: 2100 / 3000 [ 70%]  (Sampling) 
Chain 1 Iteration: 2400 / 3000 [ 80%]  (Sampling) 
Chain 2 Iteration: 2300 / 3000 [ 76%]  (Sampling) 
Chain 3 Iteration: 2400 / 3000 [ 80%]  (Sampling) 
Chain 3 Iteration: 2500 / 3000 [ 83%]  (Sampling) 
Chain 4 Iteration: 2200 / 3000 [ 73%]  (Sampling) 
Chain 1 Iteration: 2500 / 3000 [ 83%]  (Sampling) 
Chain 1 Iteration: 2600 / 3000 [ 86%]  (Sampling) 
Chain 2 Iteration: 2400 / 3000 [ 80%]  (Sampling) 
Chain 2 Iteration: 2500 / 3000 [ 83%]  (Sampling) 
Chain 3 Iteration: 2600 / 3000 [ 86%]  (Sampling) 
Chain 3 Iteration: 2700 / 3000 [ 90%]  (Sampling) 
Chain 3 Iteration: 2800 / 3000 [ 93%]  (Sampling) 
Chain 4 Iteration: 2300 / 3000 [ 76%]  (Sampling) 
Chain 4 Iteration: 2400 / 3000 [ 80%]  (Sampling) 
Chain 4 Iteration: 2500 / 3000 [ 83%]  (Sampling) 
Chain 1 Iteration: 2700 / 3000 [ 90%]  (Sampling) 
Chain 1 Iteration: 2800 / 3000 [ 93%]  (Sampling) 
Chain 1 Iteration: 2900 / 3000 [ 96%]  (Sampling) 
Chain 2 Iteration: 2600 / 3000 [ 86%]  (Sampling) 
Chain 2 Iteration: 2700 / 3000 [ 90%]  (Sampling) 
Chain 3 Iteration: 2900 / 3000 [ 96%]  (Sampling) 
Chain 4 Iteration: 2600 / 3000 [ 86%]  (Sampling) 
Chain 1 Iteration: 3000 / 3000 [100%]  (Sampling) 
Chain 2 Iteration: 2800 / 3000 [ 93%]  (Sampling) 
Chain 2 Iteration: 2900 / 3000 [ 96%]  (Sampling) 
Chain 3 Iteration: 3000 / 3000 [100%]  (Sampling) 
Chain 4 Iteration: 2700 / 3000 [ 90%]  (Sampling) 
Chain 4 Iteration: 2800 / 3000 [ 93%]  (Sampling) 
Chain 1 finished in 1.7 seconds.
Chain 3 finished in 1.6 seconds.
Chain 2 Iteration: 3000 / 3000 [100%]  (Sampling) 
Chain 4 Iteration: 2900 / 3000 [ 96%]  (Sampling) 
Chain 4 Iteration: 3000 / 3000 [100%]  (Sampling) 
Chain 2 finished in 1.8 seconds.
Chain 4 finished in 1.8 seconds.

All 4 chains finished successfully.
Mean chain execution time: 1.7 seconds.
Total execution time: 1.9 seconds.

fit4b$summary()

# A tibble: 8 × 10
  variable       mean   median    sd   mad       q5       q95  rhat ess_bulk
  <chr>         <dbl>    <dbl> <dbl> <dbl>    <dbl>     <dbl> <dbl>    <dbl>
1 lp__       -157.    -157.    1.95  1.85  -161.    -154.      1.00    4215.
2 alpha_1[1]    2.45     2.46  0.292 0.284    1.95     2.90    1.00    8685.
3 alpha_1[2]    3.85     3.85  0.254 0.256    3.42     4.26    1.00    9349.
4 sigma_x       1.75     1.74  0.181 0.175    1.48     2.07    1.00    8116.
5 beta_1[1]     0.760    0.758 0.530 0.536   -0.102    1.65    1.00    6824.
6 beta_1[2]     1.45     1.40  1.17  1.15    -0.351    3.47    1.00    5524.
7 beta_2[1]    -0.397   -0.392 0.197 0.197   -0.732   -0.0818  1.00    6880.
8 beta_2[2]    -1.69    -1.61  0.666 0.640   -2.94    -0.752   1.00    5384.
# ℹ 1 more variable: ess_tail <dbl>

str(sim2_parms)

List of 7
 $ n      : num 116
 $ a1     : num [1:2] 2.5 4
 $ b1     : num [1:2] 1.7 2.2
 $ b2     : num [1:2] -0.67 -1.37
 $ sigma_x: num 1.5
 $ LoD    : num 3
 $ latent : logi TRUE

fit_summary <- fit4b$summary() |>
    dplyr::select(variable, median, q5, q95) |>
    dplyr::filter(variable != "lp__") |>
    dplyr::mutate(
        truth = c(
            #sim2_parms$a0,
            sim2_parms$a1[[1]],
            sim2_parms$a1[[2]],
            sim2_parms$sigma_x,
            #sim2_parms$b0,
            sim2_parms$b1[[1]],
            sim2_parms$b1[[2]],
            sim2_parms$b2[[1]],
            sim2_parms$b2[[2]]
        )
    )

po <-
    ggplot(fit_summary) +
    aes(x = variable, y = median, ymin = q5, ymax = q95) +
    geom_hline(yintercept = 0, linetype = "dashed", color = "gray") +
    geom_pointrange() +
    geom_point(aes(y = truth), shape = 4, color = "red", size = 3, stroke = 1) +
    labs(
        x = NULL,
        y = "Parameter value",
        title = "Model-estimated median with 95% CI; x marks true simulation value",
        subtitle = "Estimated with observed (censored) values with correction"
    )

6.3 Model if x was not censored

mod4b_data_l <- sim_data_4b |>
    dplyr::mutate(x_l = -9999, t = as.integer(t)) |>
    dplyr::select(t, y, x = x_star, x_l) |>
    as.list()

mod4b_data_l <- c(
    "N" = nrow(sim_data_4b),
    "k" = as.integer(max(mod4b_data_l$t)),
    mod4b_data_l
)
str(mod4b_data_l)

List of 6
 $ N  : int 116
 $ k  : int 2
 $ t  : int [1:116] 1 1 2 1 1 1 2 2 2 2 ...
 $ y  : int [1:116] 1 0 0 0 0 0 0 0 0 0 ...
 $ x  : num [1:116] 2.07 3.19 2.2 3.79 4.7 ...
 $ x_l: num [1:116] -9999 -9999 -9999 -9999 -9999 ...

fit4b_l <- mod4b$sample(
    mod4b_data_l,
    seed = 5234521,
    parallel_chains = 4,
    iter_warmup = 500,
    iter_sampling = 2500,
    show_messages = T
)

Running MCMC with 4 parallel chains...

Chain 1 Iteration:    1 / 3000 [  0%]  (Warmup) 
Chain 1 Iteration:  100 / 3000 [  3%]  (Warmup) 
Chain 2 Iteration:    1 / 3000 [  0%]  (Warmup) 
Chain 2 Iteration:  100 / 3000 [  3%]  (Warmup) 
Chain 3 Iteration:    1 / 3000 [  0%]  (Warmup) 
Chain 3 Iteration:  100 / 3000 [  3%]  (Warmup) 
Chain 4 Iteration:    1 / 3000 [  0%]  (Warmup) 
Chain 4 Iteration:  100 / 3000 [  3%]  (Warmup) 
Chain 1 Iteration:  200 / 3000 [  6%]  (Warmup) 
Chain 1 Iteration:  300 / 3000 [ 10%]  (Warmup) 
Chain 1 Iteration:  400 / 3000 [ 13%]  (Warmup) 
Chain 1 Iteration:  500 / 3000 [ 16%]  (Warmup) 
Chain 1 Iteration:  501 / 3000 [ 16%]  (Sampling) 
Chain 1 Iteration:  600 / 3000 [ 20%]  (Sampling) 
Chain 2 Iteration:  200 / 3000 [  6%]  (Warmup) 
Chain 2 Iteration:  300 / 3000 [ 10%]  (Warmup) 
Chain 2 Iteration:  400 / 3000 [ 13%]  (Warmup) 
Chain 2 Iteration:  500 / 3000 [ 16%]  (Warmup) 
Chain 2 Iteration:  501 / 3000 [ 16%]  (Sampling) 
Chain 2 Iteration:  600 / 3000 [ 20%]  (Sampling) 
Chain 3 Iteration:  200 / 3000 [  6%]  (Warmup) 
Chain 3 Iteration:  300 / 3000 [ 10%]  (Warmup) 
Chain 3 Iteration:  400 / 3000 [ 13%]  (Warmup) 
Chain 3 Iteration:  500 / 3000 [ 16%]  (Warmup) 
Chain 3 Iteration:  501 / 3000 [ 16%]  (Sampling) 
Chain 3 Iteration:  600 / 3000 [ 20%]  (Sampling) 
Chain 4 Iteration:  200 / 3000 [  6%]  (Warmup) 
Chain 4 Iteration:  300 / 3000 [ 10%]  (Warmup) 
Chain 4 Iteration:  400 / 3000 [ 13%]  (Warmup) 
Chain 4 Iteration:  500 / 3000 [ 16%]  (Warmup) 
Chain 4 Iteration:  501 / 3000 [ 16%]  (Sampling) 
Chain 1 Iteration:  700 / 3000 [ 23%]  (Sampling) 
Chain 1 Iteration:  800 / 3000 [ 26%]  (Sampling) 
Chain 1 Iteration:  900 / 3000 [ 30%]  (Sampling) 
Chain 2 Iteration:  700 / 3000 [ 23%]  (Sampling) 
Chain 2 Iteration:  800 / 3000 [ 26%]  (Sampling) 
Chain 2 Iteration:  900 / 3000 [ 30%]  (Sampling) 
Chain 3 Iteration:  700 / 3000 [ 23%]  (Sampling) 
Chain 3 Iteration:  800 / 3000 [ 26%]  (Sampling) 
Chain 3 Iteration:  900 / 3000 [ 30%]  (Sampling) 
Chain 4 Iteration:  600 / 3000 [ 20%]  (Sampling) 
Chain 4 Iteration:  700 / 3000 [ 23%]  (Sampling) 
Chain 4 Iteration:  800 / 3000 [ 26%]  (Sampling) 
Chain 1 Iteration: 1000 / 3000 [ 33%]  (Sampling) 
Chain 1 Iteration: 1100 / 3000 [ 36%]  (Sampling) 
Chain 2 Iteration: 1000 / 3000 [ 33%]  (Sampling) 
Chain 2 Iteration: 1100 / 3000 [ 36%]  (Sampling) 
Chain 3 Iteration: 1000 / 3000 [ 33%]  (Sampling) 
Chain 3 Iteration: 1100 / 3000 [ 36%]  (Sampling) 
Chain 4 Iteration:  900 / 3000 [ 30%]  (Sampling) 
Chain 4 Iteration: 1000 / 3000 [ 33%]  (Sampling) 
Chain 1 Iteration: 1200 / 3000 [ 40%]  (Sampling) 
Chain 1 Iteration: 1300 / 3000 [ 43%]  (Sampling) 
Chain 1 Iteration: 1400 / 3000 [ 46%]  (Sampling) 
Chain 2 Iteration: 1200 / 3000 [ 40%]  (Sampling) 
Chain 2 Iteration: 1300 / 3000 [ 43%]  (Sampling) 
Chain 3 Iteration: 1200 / 3000 [ 40%]  (Sampling) 
Chain 3 Iteration: 1300 / 3000 [ 43%]  (Sampling) 
Chain 4 Iteration: 1100 / 3000 [ 36%]  (Sampling) 
Chain 4 Iteration: 1200 / 3000 [ 40%]  (Sampling) 
Chain 1 Iteration: 1500 / 3000 [ 50%]  (Sampling) 
Chain 1 Iteration: 1600 / 3000 [ 53%]  (Sampling) 
Chain 2 Iteration: 1400 / 3000 [ 46%]  (Sampling) 
Chain 2 Iteration: 1500 / 3000 [ 50%]  (Sampling) 
Chain 3 Iteration: 1400 / 3000 [ 46%]  (Sampling) 
Chain 3 Iteration: 1500 / 3000 [ 50%]  (Sampling) 
Chain 4 Iteration: 1300 / 3000 [ 43%]  (Sampling) 
Chain 4 Iteration: 1400 / 3000 [ 46%]  (Sampling) 
Chain 1 Iteration: 1700 / 3000 [ 56%]  (Sampling) 
Chain 1 Iteration: 1800 / 3000 [ 60%]  (Sampling) 
Chain 1 Iteration: 1900 / 3000 [ 63%]  (Sampling) 
Chain 2 Iteration: 1600 / 3000 [ 53%]  (Sampling) 
Chain 2 Iteration: 1700 / 3000 [ 56%]  (Sampling) 
Chain 3 Iteration: 1600 / 3000 [ 53%]  (Sampling) 
Chain 3 Iteration: 1700 / 3000 [ 56%]  (Sampling) 
Chain 3 Iteration: 1800 / 3000 [ 60%]  (Sampling) 
Chain 4 Iteration: 1500 / 3000 [ 50%]  (Sampling) 
Chain 4 Iteration: 1600 / 3000 [ 53%]  (Sampling) 
Chain 1 Iteration: 2000 / 3000 [ 66%]  (Sampling) 
Chain 1 Iteration: 2100 / 3000 [ 70%]  (Sampling) 
Chain 2 Iteration: 1800 / 3000 [ 60%]  (Sampling) 
Chain 2 Iteration: 1900 / 3000 [ 63%]  (Sampling) 
Chain 3 Iteration: 1900 / 3000 [ 63%]  (Sampling) 
Chain 3 Iteration: 2000 / 3000 [ 66%]  (Sampling) 
Chain 4 Iteration: 1700 / 3000 [ 56%]  (Sampling) 
Chain 4 Iteration: 1800 / 3000 [ 60%]  (Sampling) 
Chain 1 Iteration: 2200 / 3000 [ 73%]  (Sampling) 
Chain 1 Iteration: 2300 / 3000 [ 76%]  (Sampling) 
Chain 2 Iteration: 2000 / 3000 [ 66%]  (Sampling) 
Chain 2 Iteration: 2100 / 3000 [ 70%]  (Sampling) 
Chain 2 Iteration: 2200 / 3000 [ 73%]  (Sampling) 
Chain 3 Iteration: 2100 / 3000 [ 70%]  (Sampling) 
Chain 3 Iteration: 2200 / 3000 [ 73%]  (Sampling) 
Chain 4 Iteration: 1900 / 3000 [ 63%]  (Sampling) 
Chain 4 Iteration: 2000 / 3000 [ 66%]  (Sampling) 
Chain 4 Iteration: 2100 / 3000 [ 70%]  (Sampling) 
Chain 1 Iteration: 2400 / 3000 [ 80%]  (Sampling) 
Chain 1 Iteration: 2500 / 3000 [ 83%]  (Sampling) 
Chain 1 Iteration: 2600 / 3000 [ 86%]  (Sampling) 
Chain 2 Iteration: 2300 / 3000 [ 76%]  (Sampling) 
Chain 2 Iteration: 2400 / 3000 [ 80%]  (Sampling) 
Chain 3 Iteration: 2300 / 3000 [ 76%]  (Sampling) 
Chain 3 Iteration: 2400 / 3000 [ 80%]  (Sampling) 
Chain 4 Iteration: 2200 / 3000 [ 73%]  (Sampling) 
Chain 4 Iteration: 2300 / 3000 [ 76%]  (Sampling) 
Chain 1 Iteration: 2700 / 3000 [ 90%]  (Sampling) 
Chain 1 Iteration: 2800 / 3000 [ 93%]  (Sampling) 
Chain 1 Iteration: 2900 / 3000 [ 96%]  (Sampling) 
Chain 2 Iteration: 2500 / 3000 [ 83%]  (Sampling) 
Chain 2 Iteration: 2600 / 3000 [ 86%]  (Sampling) 
Chain 2 Iteration: 2700 / 3000 [ 90%]  (Sampling) 
Chain 3 Iteration: 2500 / 3000 [ 83%]  (Sampling) 
Chain 3 Iteration: 2600 / 3000 [ 86%]  (Sampling) 
Chain 4 Iteration: 2400 / 3000 [ 80%]  (Sampling) 
Chain 4 Iteration: 2500 / 3000 [ 83%]  (Sampling) 
Chain 4 Iteration: 2600 / 3000 [ 86%]  (Sampling) 
Chain 1 Iteration: 3000 / 3000 [100%]  (Sampling) 
Chain 2 Iteration: 2800 / 3000 [ 93%]  (Sampling) 
Chain 2 Iteration: 2900 / 3000 [ 96%]  (Sampling) 
Chain 3 Iteration: 2700 / 3000 [ 90%]  (Sampling) 
Chain 3 Iteration: 2800 / 3000 [ 93%]  (Sampling) 
Chain 4 Iteration: 2700 / 3000 [ 90%]  (Sampling) 
Chain 4 Iteration: 2800 / 3000 [ 93%]  (Sampling) 
Chain 1 finished in 1.4 seconds.
Chain 2 Iteration: 3000 / 3000 [100%]  (Sampling) 
Chain 3 Iteration: 2900 / 3000 [ 96%]  (Sampling) 
Chain 3 Iteration: 3000 / 3000 [100%]  (Sampling) 
Chain 4 Iteration: 2900 / 3000 [ 96%]  (Sampling) 
Chain 4 Iteration: 3000 / 3000 [100%]  (Sampling) 
Chain 2 finished in 1.5 seconds.
Chain 3 finished in 1.5 seconds.
Chain 4 finished in 1.5 seconds.

All 4 chains finished successfully.
Mean chain execution time: 1.5 seconds.
Total execution time: 1.6 seconds.

fit4b_l$summary()

# A tibble: 8 × 10
  variable       mean   median    sd   mad       q5      q95  rhat ess_bulk
  <chr>         <dbl>    <dbl> <dbl> <dbl>    <dbl>    <dbl> <dbl>    <dbl>
1 lp__       -166.    -165.    1.87  1.73  -169.    -163.     1.00    4661.
2 alpha_1[1]    2.63     2.64  0.204 0.203    2.30     2.97   1.00   11142.
3 alpha_1[2]    3.90     3.91  0.214 0.213    3.55     4.25   1.00   12564.
4 sigma_x       1.61     1.61  0.108 0.108    1.44     1.79   1.00   10927.
5 beta_1[1]     1.50     1.48  0.599 0.597    0.545    2.51   1.00    7405.
6 beta_1[2]     1.21     1.19  1.09  1.09    -0.530    3.06   1.00    7679.
7 beta_2[1]    -0.673   -0.661 0.213 0.216   -1.04    -0.342  1.00    7502.
8 beta_2[2]    -1.26    -1.22  0.449 0.446   -2.06    -0.603  1.00    7520.
# ℹ 1 more variable: ess_tail <dbl>

str(sim2_parms)

List of 7
 $ n      : num 116
 $ a1     : num [1:2] 2.5 4
 $ b1     : num [1:2] 1.7 2.2
 $ b2     : num [1:2] -0.67 -1.37
 $ sigma_x: num 1.5
 $ LoD    : num 3
 $ latent : logi TRUE

fit_summary_l <- fit4b_l$summary() |>
    dplyr::select(variable, median, q5, q95) |>
    dplyr::filter(variable != "lp__") |>
    dplyr::mutate(
        truth = c(
            #sim2_parms$a0,
            sim2_parms$a1[[1]],
            sim2_parms$a1[[2]],
            sim2_parms$sigma_x,
            #sim2_parms$b0,
            sim2_parms$b1[[1]],
            sim2_parms$b1[[2]],
            sim2_parms$b2[[1]],
            sim2_parms$b2[[2]]
        )
    )

pl <-
    ggplot(fit_summary_l) +
    aes(x = variable, y = median, ymin = q5, ymax = q95) +
    geom_hline(yintercept = 0, linetype = "dashed", color = "gray") +
    geom_pointrange() +
    geom_point(aes(y = truth), shape = 4, color = "red", size = 3, stroke = 1) +
    labs(
        x = NULL,
        y = "Parameter value",
        title = "Model-estimated median with 95% CI; x marks true simulation value",
        subtitle = "Estimated using true latent values"
    )

6.4 Do it the naive way

mod4b_data_n <- sim_data_4b |>
    dplyr::mutate(x_l = -9999, t = as.integer(t)) |>
    dplyr::select(t, y, x = x, x_l) |>
    as.list()

mod4b_data_n <- c(
    "N" = nrow(sim_data_4b),
    "k" = as.integer(max(mod4b_data_n$t)),
    mod4b_data_n
)
str(mod4b_data_n)

List of 6
 $ N  : int 116
 $ k  : int 2
 $ t  : int [1:116] 1 1 2 1 1 1 2 2 2 2 ...
 $ y  : int [1:116] 1 0 0 0 0 0 0 0 0 0 ...
 $ x  : num [1:116] 1.5 3.19 1.5 3.79 4.7 ...
 $ x_l: num [1:116] -9999 -9999 -9999 -9999 -9999 ...

fit4b_n <- mod4b$sample(
    mod4b_data_n,
    seed = 873215,
    parallel_chains = 4,
    iter_warmup = 500,
    iter_sampling = 2500,
    show_messages = T
)

Running MCMC with 4 parallel chains...

Chain 1 Iteration:    1 / 3000 [  0%]  (Warmup) 
Chain 1 Iteration:  100 / 3000 [  3%]  (Warmup) 
Chain 2 Iteration:    1 / 3000 [  0%]  (Warmup) 
Chain 2 Iteration:  100 / 3000 [  3%]  (Warmup) 
Chain 3 Iteration:    1 / 3000 [  0%]  (Warmup) 
Chain 3 Iteration:  100 / 3000 [  3%]  (Warmup) 
Chain 4 Iteration:    1 / 3000 [  0%]  (Warmup) 
Chain 4 Iteration:  100 / 3000 [  3%]  (Warmup) 
Chain 1 Iteration:  200 / 3000 [  6%]  (Warmup) 
Chain 1 Iteration:  300 / 3000 [ 10%]  (Warmup) 
Chain 1 Iteration:  400 / 3000 [ 13%]  (Warmup) 
Chain 1 Iteration:  500 / 3000 [ 16%]  (Warmup) 
Chain 1 Iteration:  501 / 3000 [ 16%]  (Sampling) 
Chain 1 Iteration:  600 / 3000 [ 20%]  (Sampling) 
Chain 2 Iteration:  200 / 3000 [  6%]  (Warmup) 
Chain 2 Iteration:  300 / 3000 [ 10%]  (Warmup) 
Chain 2 Iteration:  400 / 3000 [ 13%]  (Warmup) 
Chain 2 Iteration:  500 / 3000 [ 16%]  (Warmup) 
Chain 2 Iteration:  501 / 3000 [ 16%]  (Sampling) 
Chain 2 Iteration:  600 / 3000 [ 20%]  (Sampling) 
Chain 3 Iteration:  200 / 3000 [  6%]  (Warmup) 
Chain 3 Iteration:  300 / 3000 [ 10%]  (Warmup) 
Chain 3 Iteration:  400 / 3000 [ 13%]  (Warmup) 
Chain 3 Iteration:  500 / 3000 [ 16%]  (Warmup) 
Chain 3 Iteration:  501 / 3000 [ 16%]  (Sampling) 
Chain 3 Iteration:  600 / 3000 [ 20%]  (Sampling) 
Chain 4 Iteration:  200 / 3000 [  6%]  (Warmup) 
Chain 4 Iteration:  300 / 3000 [ 10%]  (Warmup) 
Chain 4 Iteration:  400 / 3000 [ 13%]  (Warmup) 
Chain 4 Iteration:  500 / 3000 [ 16%]  (Warmup) 
Chain 4 Iteration:  501 / 3000 [ 16%]  (Sampling) 
Chain 1 Iteration:  700 / 3000 [ 23%]  (Sampling) 
Chain 1 Iteration:  800 / 3000 [ 26%]  (Sampling) 
Chain 1 Iteration:  900 / 3000 [ 30%]  (Sampling) 
Chain 2 Iteration:  700 / 3000 [ 23%]  (Sampling) 
Chain 2 Iteration:  800 / 3000 [ 26%]  (Sampling) 
Chain 2 Iteration:  900 / 3000 [ 30%]  (Sampling) 
Chain 3 Iteration:  700 / 3000 [ 23%]  (Sampling) 
Chain 3 Iteration:  800 / 3000 [ 26%]  (Sampling) 
Chain 3 Iteration:  900 / 3000 [ 30%]  (Sampling) 
Chain 4 Iteration:  600 / 3000 [ 20%]  (Sampling) 
Chain 4 Iteration:  700 / 3000 [ 23%]  (Sampling) 
Chain 4 Iteration:  800 / 3000 [ 26%]  (Sampling) 
Chain 1 Iteration: 1000 / 3000 [ 33%]  (Sampling) 
Chain 1 Iteration: 1100 / 3000 [ 36%]  (Sampling) 
Chain 2 Iteration: 1000 / 3000 [ 33%]  (Sampling) 
Chain 2 Iteration: 1100 / 3000 [ 36%]  (Sampling) 
Chain 3 Iteration: 1000 / 3000 [ 33%]  (Sampling) 
Chain 3 Iteration: 1100 / 3000 [ 36%]  (Sampling) 
Chain 4 Iteration:  900 / 3000 [ 30%]  (Sampling) 
Chain 4 Iteration: 1000 / 3000 [ 33%]  (Sampling) 
Chain 1 Iteration: 1200 / 3000 [ 40%]  (Sampling) 
Chain 1 Iteration: 1300 / 3000 [ 43%]  (Sampling) 
Chain 2 Iteration: 1200 / 3000 [ 40%]  (Sampling) 
Chain 2 Iteration: 1300 / 3000 [ 43%]  (Sampling) 
Chain 3 Iteration: 1200 / 3000 [ 40%]  (Sampling) 
Chain 3 Iteration: 1300 / 3000 [ 43%]  (Sampling) 
Chain 4 Iteration: 1100 / 3000 [ 36%]  (Sampling) 
Chain 4 Iteration: 1200 / 3000 [ 40%]  (Sampling) 
Chain 1 Iteration: 1400 / 3000 [ 46%]  (Sampling) 
Chain 1 Iteration: 1500 / 3000 [ 50%]  (Sampling) 
Chain 2 Iteration: 1400 / 3000 [ 46%]  (Sampling) 
Chain 2 Iteration: 1500 / 3000 [ 50%]  (Sampling) 
Chain 3 Iteration: 1400 / 3000 [ 46%]  (Sampling) 
Chain 3 Iteration: 1500 / 3000 [ 50%]  (Sampling) 
Chain 4 Iteration: 1300 / 3000 [ 43%]  (Sampling) 
Chain 4 Iteration: 1400 / 3000 [ 46%]  (Sampling) 
Chain 1 Iteration: 1600 / 3000 [ 53%]  (Sampling) 
Chain 1 Iteration: 1700 / 3000 [ 56%]  (Sampling) 
Chain 2 Iteration: 1600 / 3000 [ 53%]  (Sampling) 
Chain 2 Iteration: 1700 / 3000 [ 56%]  (Sampling) 
Chain 3 Iteration: 1600 / 3000 [ 53%]  (Sampling) 
Chain 3 Iteration: 1700 / 3000 [ 56%]  (Sampling) 
Chain 4 Iteration: 1500 / 3000 [ 50%]  (Sampling) 
Chain 4 Iteration: 1600 / 3000 [ 53%]  (Sampling) 
Chain 4 Iteration: 1700 / 3000 [ 56%]  (Sampling) 
Chain 1 Iteration: 1800 / 3000 [ 60%]  (Sampling) 
Chain 1 Iteration: 1900 / 3000 [ 63%]  (Sampling) 
Chain 2 Iteration: 1800 / 3000 [ 60%]  (Sampling) 
Chain 2 Iteration: 1900 / 3000 [ 63%]  (Sampling) 
Chain 2 Iteration: 2000 / 3000 [ 66%]  (Sampling) 
Chain 3 Iteration: 1800 / 3000 [ 60%]  (Sampling) 
Chain 3 Iteration: 1900 / 3000 [ 63%]  (Sampling) 
Chain 4 Iteration: 1800 / 3000 [ 60%]  (Sampling) 
Chain 4 Iteration: 1900 / 3000 [ 63%]  (Sampling) 
Chain 1 Iteration: 2000 / 3000 [ 66%]  (Sampling) 
Chain 1 Iteration: 2100 / 3000 [ 70%]  (Sampling) 
Chain 2 Iteration: 2100 / 3000 [ 70%]  (Sampling) 
Chain 2 Iteration: 2200 / 3000 [ 73%]  (Sampling) 
Chain 3 Iteration: 2000 / 3000 [ 66%]  (Sampling) 
Chain 3 Iteration: 2100 / 3000 [ 70%]  (Sampling) 
Chain 4 Iteration: 2000 / 3000 [ 66%]  (Sampling) 
Chain 4 Iteration: 2100 / 3000 [ 70%]  (Sampling) 
Chain 1 Iteration: 2200 / 3000 [ 73%]  (Sampling) 
Chain 1 Iteration: 2300 / 3000 [ 76%]  (Sampling) 
Chain 2 Iteration: 2300 / 3000 [ 76%]  (Sampling) 
Chain 2 Iteration: 2400 / 3000 [ 80%]  (Sampling) 
Chain 2 Iteration: 2500 / 3000 [ 83%]  (Sampling) 
Chain 3 Iteration: 2200 / 3000 [ 73%]  (Sampling) 
Chain 3 Iteration: 2300 / 3000 [ 76%]  (Sampling) 
Chain 4 Iteration: 2200 / 3000 [ 73%]  (Sampling) 
Chain 4 Iteration: 2300 / 3000 [ 76%]  (Sampling) 
Chain 1 Iteration: 2400 / 3000 [ 80%]  (Sampling) 
Chain 1 Iteration: 2500 / 3000 [ 83%]  (Sampling) 
Chain 1 Iteration: 2600 / 3000 [ 86%]  (Sampling) 
Chain 2 Iteration: 2600 / 3000 [ 86%]  (Sampling) 
Chain 2 Iteration: 2700 / 3000 [ 90%]  (Sampling) 
Chain 3 Iteration: 2400 / 3000 [ 80%]  (Sampling) 
Chain 3 Iteration: 2500 / 3000 [ 83%]  (Sampling) 
Chain 3 Iteration: 2600 / 3000 [ 86%]  (Sampling) 
Chain 4 Iteration: 2400 / 3000 [ 80%]  (Sampling) 
Chain 4 Iteration: 2500 / 3000 [ 83%]  (Sampling) 
Chain 1 Iteration: 2700 / 3000 [ 90%]  (Sampling) 
Chain 1 Iteration: 2800 / 3000 [ 93%]  (Sampling) 
Chain 2 Iteration: 2800 / 3000 [ 93%]  (Sampling) 
Chain 2 Iteration: 2900 / 3000 [ 96%]  (Sampling) 
Chain 2 Iteration: 3000 / 3000 [100%]  (Sampling) 
Chain 3 Iteration: 2700 / 3000 [ 90%]  (Sampling) 
Chain 3 Iteration: 2800 / 3000 [ 93%]  (Sampling) 
Chain 4 Iteration: 2600 / 3000 [ 86%]  (Sampling) 
Chain 4 Iteration: 2700 / 3000 [ 90%]  (Sampling) 
Chain 4 Iteration: 2800 / 3000 [ 93%]  (Sampling) 
Chain 2 finished in 1.5 seconds.
Chain 1 Iteration: 2900 / 3000 [ 96%]  (Sampling) 
Chain 1 Iteration: 3000 / 3000 [100%]  (Sampling) 
Chain 3 Iteration: 2900 / 3000 [ 96%]  (Sampling) 
Chain 3 Iteration: 3000 / 3000 [100%]  (Sampling) 
Chain 4 Iteration: 2900 / 3000 [ 96%]  (Sampling) 
Chain 4 Iteration: 3000 / 3000 [100%]  (Sampling) 
Chain 1 finished in 1.6 seconds.
Chain 3 finished in 1.5 seconds.
Chain 4 finished in 1.6 seconds.

All 4 chains finished successfully.
Mean chain execution time: 1.5 seconds.
Total execution time: 1.7 seconds.

fit4b_n$summary()

# A tibble: 8 × 10
  variable       mean   median    sd   mad        q5       q95  rhat ess_bulk
  <chr>         <dbl>    <dbl> <dbl> <dbl>     <dbl>     <dbl> <dbl>    <dbl>
1 lp__       -170.    -169.    1.89  1.73  -173.     -167.      1.00    4136.
2 alpha_1[1]    2.53     2.53  0.209 0.204    2.19      2.87    1.00   10825.
3 alpha_1[2]    3.75     3.75  0.217 0.215    3.39      4.11    1.00   10929.
4 sigma_x       1.63     1.62  0.107 0.106    1.46      1.81    1.00   10108.
5 beta_1[1]     0.776    0.768 0.521 0.522   -0.0606    1.64    1.00    6724.
6 beta_1[2]     1.45     1.40  1.17  1.13    -0.390     3.46    1.00    6954.
7 beta_2[1]    -0.404   -0.396 0.194 0.191   -0.731    -0.0970  1.00    6755.
8 beta_2[2]    -1.69    -1.61  0.666 0.649   -2.92     -0.748   1.00    6854.
# ℹ 1 more variable: ess_tail <dbl>

str(sim2_parms)

List of 7
 $ n      : num 116
 $ a1     : num [1:2] 2.5 4
 $ b1     : num [1:2] 1.7 2.2
 $ b2     : num [1:2] -0.67 -1.37
 $ sigma_x: num 1.5
 $ LoD    : num 3
 $ latent : logi TRUE

fit_summary_n <- fit4b_n$summary() |>
    dplyr::select(variable, median, q5, q95) |>
    dplyr::filter(variable != "lp__") |>
    dplyr::mutate(
        truth = c(
            #sim2_parms$a0,
            sim2_parms$a1[[1]],
            sim2_parms$a1[[2]],
            sim2_parms$sigma_x,
            #sim2_parms$b0,
            sim2_parms$b1[[1]],
            sim2_parms$b1[[2]],
            sim2_parms$b2[[1]],
            sim2_parms$b2[[2]]
        )
    )

pn <-
    ggplot(fit_summary_n) +
    aes(x = variable, y = median, ymin = q5, ymax = q95) +
    geom_hline(yintercept = 0, linetype = "dashed", color = "gray") +
    geom_pointrange() +
    geom_point(aes(y = truth), shape = 4, color = "red", size = 3, stroke = 1) +
    labs(
        x = NULL,
        y = "Parameter value",
        title = "Model-estimated median with 95% CI; x marks true simulation value",
        subtitle = "Estimated using censored values without censoring correction"
    )

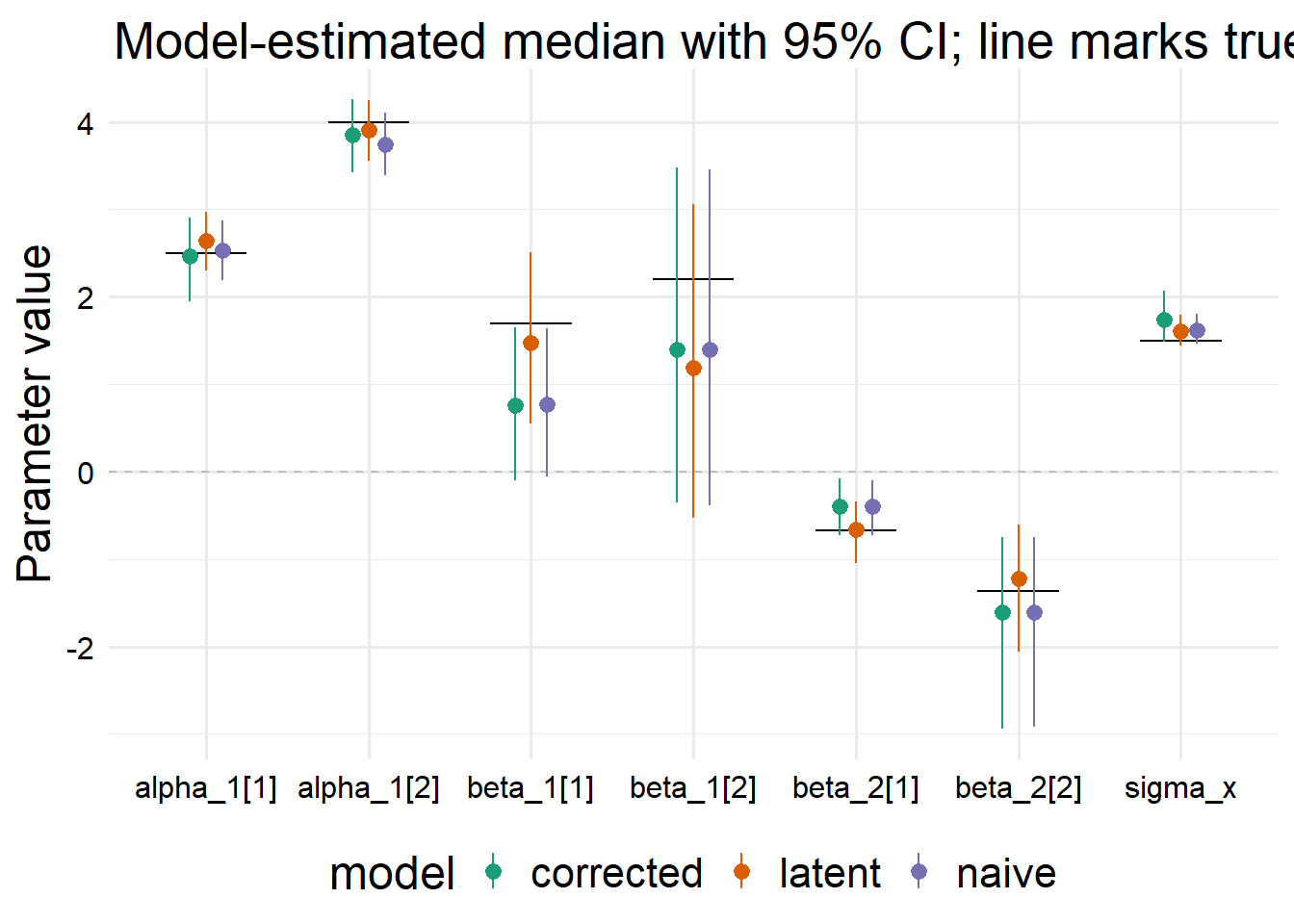
po / pl / pn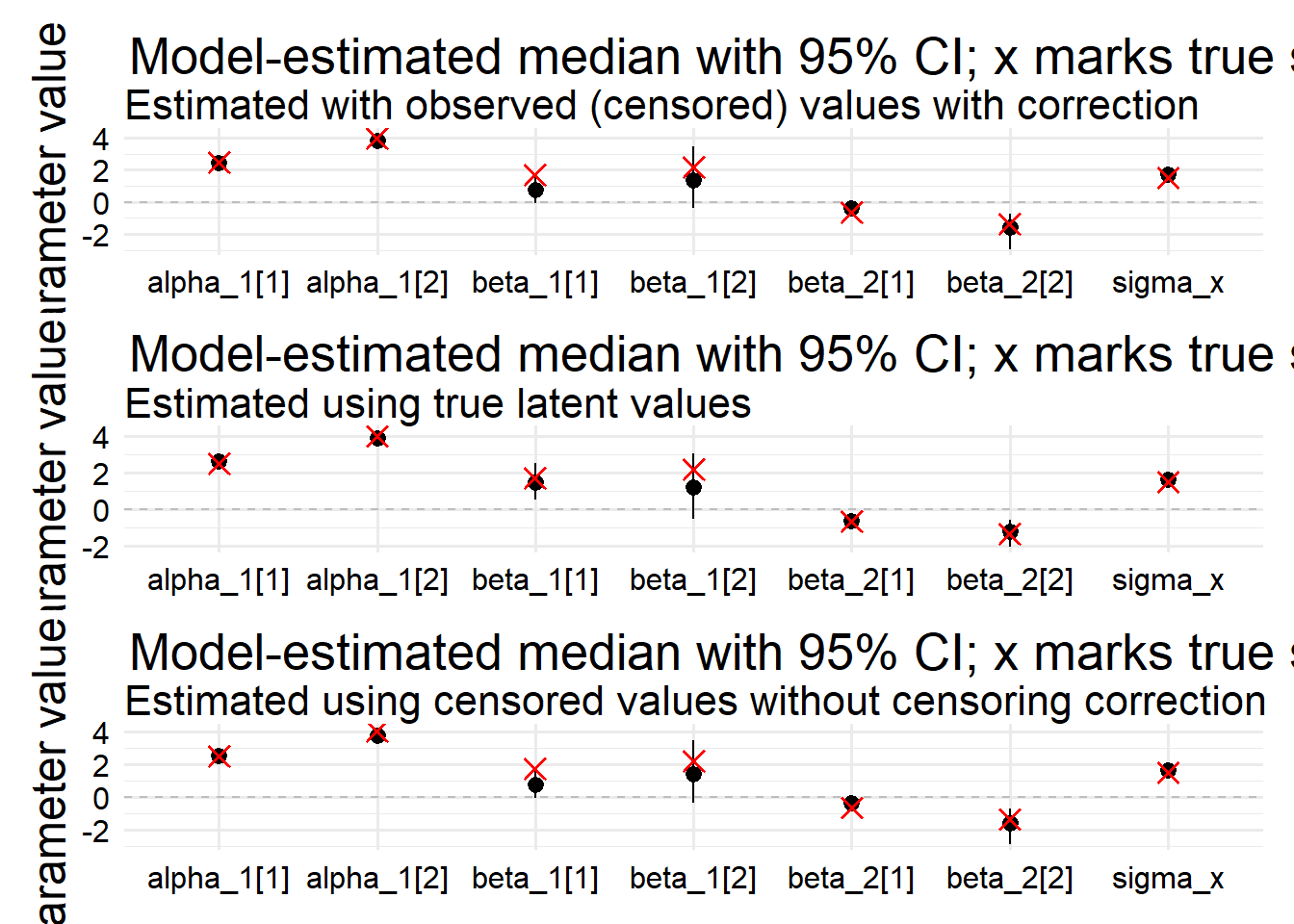

all_fits <-
    dplyr::bind_rows(
        "corrected" = fit_summary,
        "latent" = fit_summary_l,
        "naive" = fit_summary_n,
        .id = "model"
    )

all_fits |>
    ggplot() +
    aes(
        x = variable, y = median, ymin = q5, ymax = q95,
        color = model
    ) +
    geom_hline(yintercept = 0, linetype = "dashed", color = "gray") +
    geom_crossbar(
        aes(y = truth, ymin = truth, ymax = truth),
        width = 0.5,
        color = "black",
        fatten = 0.1
    ) +
    geom_pointrange(position = position_dodge2(width = 0.3)) +
    scale_color_brewer(palette = "Dark2") +
    labs(
        x = NULL,
        y = "Parameter value",
        title = "Model-estimated median with 95% CI; line marks true value"
    )

6.5 Model exploration

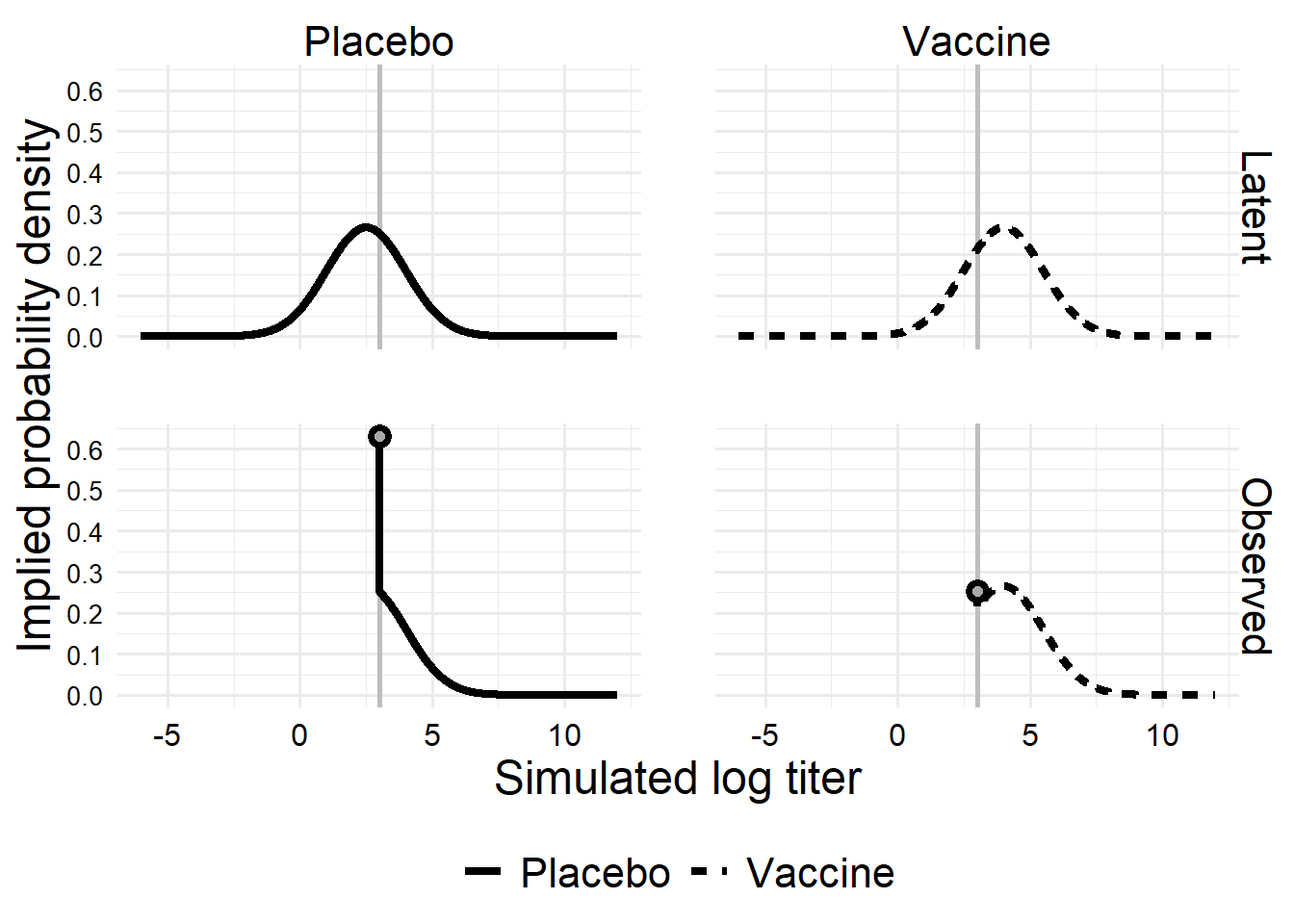
these curves are implied by the model and parameters, not by the simulated data ::: {.cell}

x_vec <- seq(-6, 12, 0.01)
r1 <- sapply(x_vec, \(x) inv_logit(1.5 + 0.2 - 0.67 * x))
r2 <- sapply(x_vec, \(x) inv_logit(1.5 + 0.7 - 1.37 * x))

layout(matrix(c(1, 2, 3, 3), ncol = 2, byrow = TRUE))
plot(x_vec, r2 - r1, ylab = "risk difference", type = "l", xlab = "")
abline(h = 0, lty = 2)
plot(x_vec, r2 / r1, ylab = "risk ratio", type = "l", xlab = "")
abline(h = 1, lty = 2)
lab2 <- latex2exp::TeX(r"($Pr(y_{i} = 1 \ | \ x_{i}, T_{i})$)")
plot(
    NULL, NULL,
    ylim = c(0, 1),
    xlim = c(-6, 12),
    yaxs = "i",
    xaxs = "i",
    xlab = "Simulated log titer",
    ylab = lab2
)
lines(x_vec, r1, lty = 2, lwd = 1.5) # placebo
lines(x_vec, r2, lty = 1, lwd = 1.5) # vaccine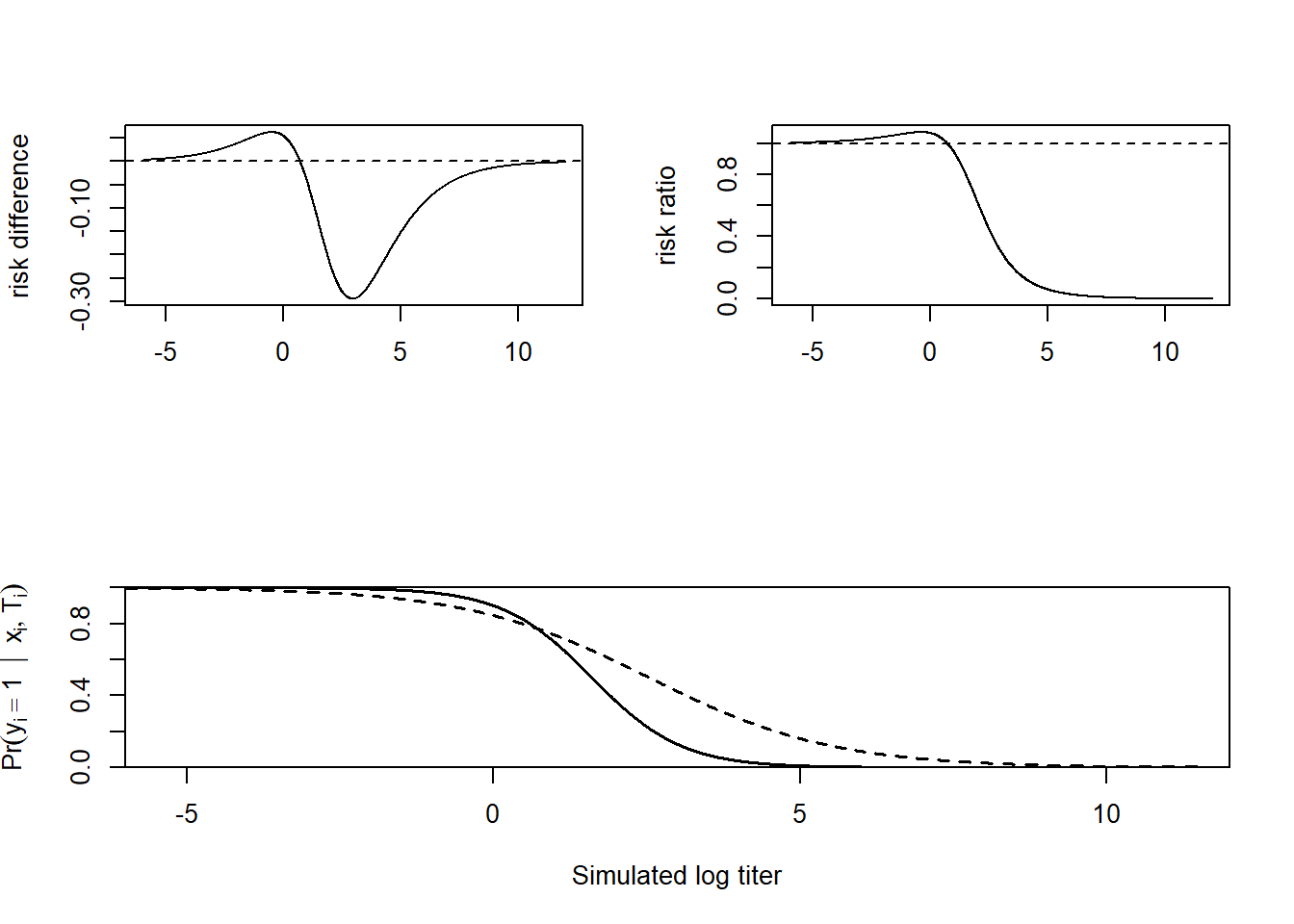

# IDK what's wrong with the legend, seems it doesn't like layout.
# switch to ggplot to fix
#legend(x = 9, y = 0.8, c('Unexposed', 'Exposed'), lty = c(2, 1), lwd = 2)

:::

x_dens <-
    tibble::tibble(
        Latent = x_vec,
        Observed = dplyr::if_else(
            x_vec < sim2_parms$LoD,
            sim2_parms$LoD,
            x_vec
        ),
        Placebo = sim2_parms$a1[1],
        Vaccine = sim2_parms$a1[2]
    ) |>
    tidyr::pivot_longer(
        cols = c(Placebo, Vaccine),
        names_to = "t",
        values_to = "mu"
    ) |>
    tidyr::pivot_longer(
        cols = c(Latent, Observed),
        names_to = "o",
        values_to = "x"
    ) |>
    dplyr::mutate(
        d = dplyr::if_else(
            o == "Latent",
            dnorm(x, mean = mu, sd = sim2_parms$sigma_x),
            crch::dcnorm(
                x, mean = mu, sd = sim2_parms$sigma_x,
                left = sim2_parms$LoD, right = Inf
            )
        )
    )

anno_df <-
    x_dens[1:4, ] |>
    dplyr::filter(o == "Observed")

x_dens |>
    ggplot() +
    aes(x = x, y = d, linetype = t, group = t) +
    geom_vline(
        xintercept = sim2_parms$LoD,
        linetype = 1, linewidth = 1, color = "gray"
    ) +
    geom_line(linewidth = 1.5) +
    geom_point(
        data = anno_df,
        size = 2,
        stroke = 2,
        shape = 21,
        color = "black",
        fill = "darkgray"
    ) +
    facet_grid(vars(o), vars(t)) +
    scale_linetype_discrete(name = NULL) +
    scale_x_continuous(breaks = scales::breaks_pretty()) +
    scale_y_continuous(breaks = scales::breaks_pretty()) +
    labs(
        x = "Simulated log titer",
        y = "Implied probability density"
    ) +
    #coord_cartesian(expand = FALSE, ylim = c(-0.01, 0.28)) +
    theme(axis.text.y = element_text(size = 10))

6.6 Try gamma dist. for x on non-logged scale?

6.7 Do we want to work out a hierarchical model?